基于LSTM的川西北地区降雨型泥石流预警方法

唐 旺, 马尚昌,陈 锐

(1.成都信息工程大学 电子工程学院(大气探测学院), 成都 610225; 2.四川省甘孜藏族自治州气象局, 四川 康定 626000)

0 引 言

川西北地区属于青藏高原的一部分,仅阿坝州境内就已形成多达200多万亩(13.33多万hm2)的干旱河谷地带,两岸山坡上几乎寸草不生,在雨季暴雨频发,极易诱发泥石流,堵塞河道,冲毁公路,危及城镇[1]。丹巴县位于甘孜藏族州境内,该地区每逢雨季地质灾害频发,泥石流是丹巴县境内主要的地质灾害之一。泥石流的发生与水有着密切关系,按照水源类型可将泥石流分为暴雨型泥石流、溃决型泥石流、冰雪融水型泥石流、泉水型泥石流等4类。从调查的结果可知, 广泛分布于丹巴县境内的254条泥石流全部属于暴雨型泥石流,没有溃决型、 冰雪融水型和泉水型泥石流。 每年汛期,受强降水天气过程的影响, 并在汇流作用下,在沟谷会发生不同程度的泥石流。 尤其是2008年以来, 受 “5·12” 汶川和 “4·20” 雅安地震的影响, 沟谷内有大量松散物源堆积,每年汛期内均有数条沟谷爆发泥石流。汛期泥石流灾害的集中发生诠释了泥石流与降雨量之间的不可分割的关系。

虽然各种自然因素都有可能引发泥石流,但降水是泥石流形成的直接触发因素[2]。 费晓燕等[3]基于降雨信息资料对四川省滑坡灾害的前期雨量进行了统计分析, 并采用逻辑回归分析建立模型,该模型的整体准确率为78.36%; 滑坡灾害的当日降雨量、前一日降雨量和前两日降雨量对灾害的影响权重分别为0.587、0.220、0.189,气象预警模型的地质背景概率和综合雨量概率的权重参数分别为0.349、0.606。江锦红等[4]从河道安全泄洪流量出发,提出了最小临界值和临界雨力的新概念和计算方法,并在此基础上构建了暴雨临界曲线作为山洪灾害预警标准。高华喜等[5]利用深圳市降雨与滑坡历史资料, 对区域性滑坡与降雨量进行相关性分析并得出结论:一次性降雨量达到或超过某一数值时区域性滑坡就可能出现,大暴雨或特大暴雨具有直接触发滑坡的作用,另外暴雨后滑坡发生可能出现滞后,滞后时间一般不超过4日。付世军等[6]基于南充市2011—2016年181条强降雨型滑坡记录,与213个自动区域站的小时雨量数据进行对比，分析了滑坡成因,确定了分县域引发滑坡的平均降雨强度与时间窗口的关系阈值,并提出了南充市强降雨诱发滑坡地质灾害风险预警技术流程框架和关键性阈值参考值。Aleotti等[7]以意大利西北部Piedmont Region 为例, 通过研究降水事件与泥石流发生之间的统计关系, 确定了该区导致泥石流发生的降水阈值。 于国强等[8]详细论述了舟曲“8·8”泥石流成灾特征和发展趋势,采用水文学分析方法,计算不同降雨频率下的洪水特征值与降雨特征值,划分地质灾害不同预警级别,提出预警判据,计算不同预警级别下的降雨特征阈值,建立前期含水量在一般和干旱两种条件下,不同预警级别的降雨历时与降雨强函数关系曲线,并阐明触发不同等级地质灾害的临界降雨特征。 温智熊等[9]通过对大量滑坡、 崩塌发生时的日降雨量、 3 日累计降雨量统计分析, 发现广西龙胜县的滑坡及崩塌发生的总数与降雨量值的大小呈折线正相关, 即降雨量值增加, 滑坡、 崩塌的数量呈台阶状增加。 Tang等[10]利用线性回归和BP神经网络对成都市地面温度进行预测, 发现神经网络的准确率高于线性回归。 疏杏胜等[11]利用ANN、 ELM以及SVM模型对桓仁水库流域未来1～3 d降雨进行多模式集成预报, 基于SVM和ELM的多模式集成预报模型预报效果均优于单一模式, 基于ANN的集成预报模型在输入因子选择合适的情况下, 其预报效果也优于单一模式, 3种模型中SVM模型对降雨预报精度改善最为明显, 说明基于机器学习模型的多模式降雨集成预报方法可行且能够提高短期预报降雨精度。 目前对于降雨阈值的研究主要分为两类, 一类是根据历史上诱发滑坡的降雨数据建立经验性降雨阈值, 另一类是通过试验方法或数值方法研究降雨对边坡稳定性的影响规律[12]。

国内外泥石流预报模型都是在长期野外监测和数据分析的基础上建立的, 所在的实验区得到了较为理想的使用[13],包括泥石流、山体滑坡、洪涝灾害等;对于地质灾害的预警预报大多使用统计的方式,即统计历史上的发生泥石流的大小与当日降雨量的数据,经过分类后给出阈值;而对于气象数据预测的研究,采用了各种神经网络在各研究区域都取得了良好的结果。但利用阈值和天气预报的协同预警,没有考虑时间、成本和复杂度的因素,因为降雨型泥石流的发生与前一段时间的降雨量都存在一定关系,而天气预报的复杂度极高且成本同样高昂,在川西北地区高原大部分地区并未设置精密的天气预报设备和装置。针对降雨型泥石流的预警,除了地质条件的影响,应该重点关注降雨量的预测,将地质灾害的预警和气象预报相结合。因此,本研究结合统计方法与LSTM方法,采用四川省甘孜藏族州丹巴县的气象数据,探寻一种针对川西北地区强降雨诱发泥石流预警的方法。

1 数据和方法

1.1 数据来源

气象数据来自于丹巴县气象监测站,主要为2010—2019年24 h降雨量、平均气温、平均相对湿度、平均风速数据，用于降雨量的预测。由于2008年汶川大地震对川西北的地质地貌产生了重大的影响,在很多地区形成了泥石流易发的沟壑、断裂等,在2010年之前同样发生了多起重大泥石流灾害。为了使阈值的划分更加科学准确,扩大样本总数以提升数据统计的可靠性,本研究统计了近20年发生的特大、大、中、小型泥石流数据,共计254条,其中特大型泥石流为6次,大型泥石流为21次,中型泥石流为102次,小型泥石流为125次。

1.2 数据初步分析

根据近20年泥石流灾害的统计数据分析,灾害活动频繁的月份在5—8月,其中6—8月占比达到91%,其原因在于每年6—8月正逢丹巴县的主汛期(图1),其中6、7月发生频率最高,总占比达到82%。丹巴县泥石流主要发生在两个时间段,分别为下午至傍晚和夜晚至次日凌晨(图2),且在凌晨发生的可能性更大。

由于数据量较大, 本文仅选取部分数据分析展示(表1)。 对泥石流灾害发生前后时段的降水量分析可知, 当降雨达到一定程度时, 将会引发泥石流灾害。 进一步地, 丹巴县泥石流的发生与1 h、 3 h、6 h、12 h、24 h、3 d、10 d的降水量有一定关系,其中与10 d的前期降雨量关系密切。小时降水量中,3 h降水所占权重较大。表2为1999年以来危害较严重的泥石流灾害发生时的前期降雨量和短时降雨量数据以及受灾情况(其中部分数据无详细发生时间, 可能与灾害统计人员的统计方式和习惯有关)。 经过分析, 当前期累积降水量(前10 d)达到50 mm以上时, 发生泥石流灾害的概率为55%; 累积降水量(前10 d)达到30 mm时发生泥石流灾害的概率为36%; 累积降水量(持续10 d)达到20 mm以上时, 发生泥石流的概率仅为9%。 小时降水量的多少与泥石流的发生有一定关系, 但无必然关系, 灾害的形成必须配合前期降水量来分析。 当12 h降水量达25～40 mm时, 泥石流发生的概率为45%； 24 h降水量达25～40 mm时, 泥石流发生的概率为9%。 经过对泥石流发生时前一段时间的降雨量统计分析,可以划分出预警的阈值,并通过不断检验和修正,得到高准确率的预警阈值。

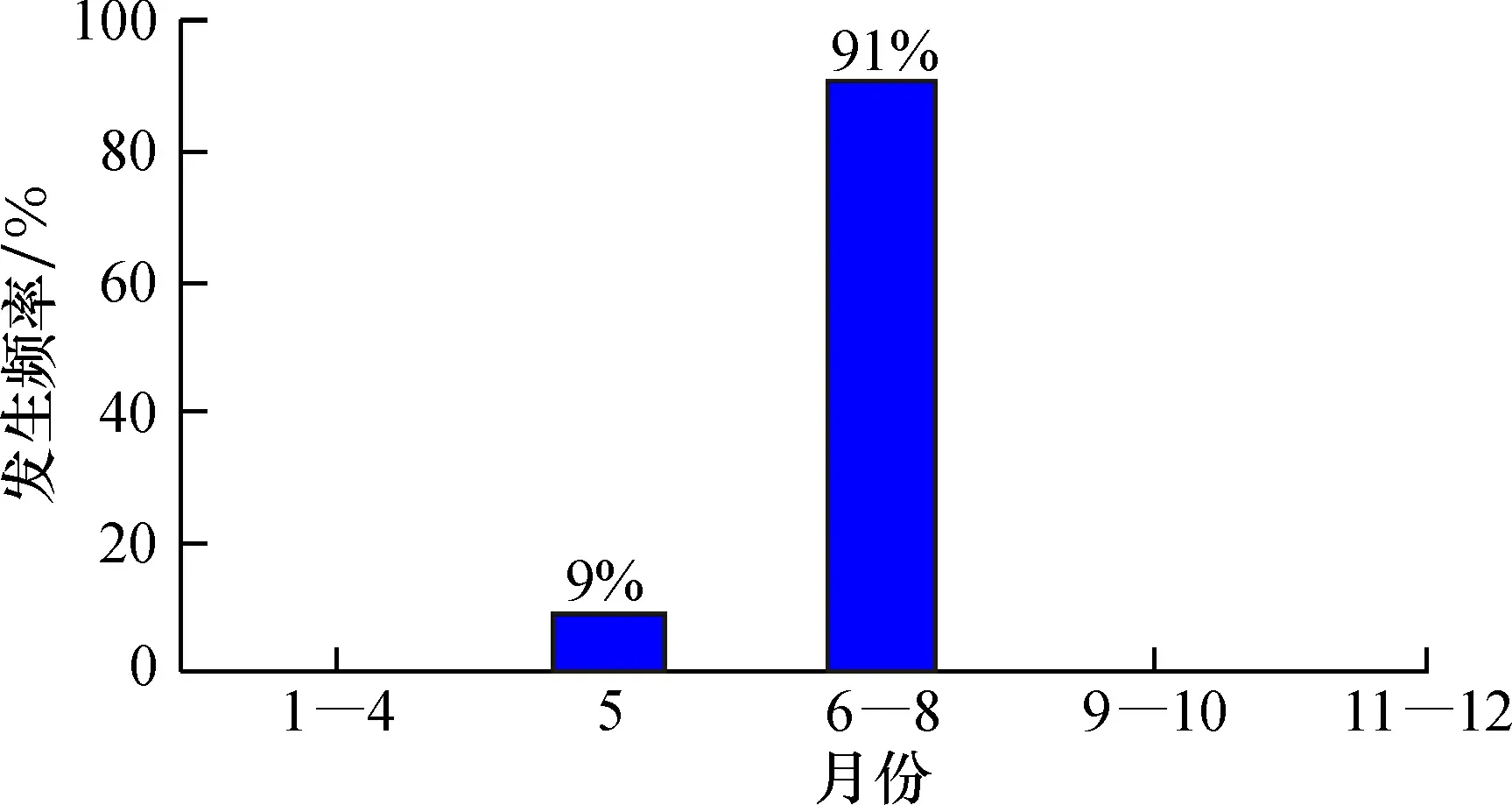
图1 丹巴县泥石流发生的月份分布

图2 丹巴县泥石流发生的时段概率分布

1.3 方法

1.3.1 长短时记忆神经网络[14]长短时记忆神经网络(long short-term memory, LSTM)相较于传统的循环神经网络(recurrent neural network,RNN)多了三道门，即“遗忘门”(forget gate)、“ 输入门”(input gate)和“输出门”(output gate), 可用以下流程和公式表示。

(1)遗忘门:t-1时刻的输入ht-1和xt经过一个线性变换+ReLU激活以后, 输出ft, 再与ct-1进行相乘得到一个中间结果。

ft=ReLU(Wf·[ht-1,xt]+bf)·ct-1。

(1)

lt=ReLU(Wi·[ht-1,xt]+bi);

(2)

(3)

(4)

(3)输出门:t-1时刻的输入ht-1和xt经过另外一个线性变换+ReLU激活以后, 输出ot;ot与ct相乘得到输出ht。

ot=ReLU(Wo·[ht-1,xt]+bo);

(5)

ht=ot·ct。

(6)

1.3.2 数据归一化 使用数据归一化能够将数据转换为0～1的数字, 在梯度下降时它可以收敛得更快。在本研究中, 使用最小-最大归一化方法来处理数据。归一化函数可描述为

表1 丹巴县部分地区泥石流发生与降水量的分布情况

表2 丹巴县部分地区泥石流灾害与前期累计和短时降水量

资料来源: 四川省丹巴县气象监测站。

(7)

其中:Xscale是归一化后的数据;X代表样本值;Xmin为样本中的最小值;Xmax为样本中的最大值。

1.3.3 精度评价 本实验采用均方误差(MSE)和平均绝对误差(MAE)作为模型预测的评价标准

(8)

(9)

2 结果分析

2.1 降雨型泥石流的阈值分析

根据近20年(1999—2019年)丹巴县泥石流灾害发生情况的统计分析, 得出了大致的阈值范围。 表3为泥石流预警等级与24 h降水量及前期累计降水量的阈值情况, 根据历史数据大致划分为5个等级, 随降雨量的增加而增加。 表4为对于泥石流发生时间的预警情况, 夜间发生泥石流的可能性最大, 如果有大的降雨发生, 那么需要在夜间之前发布预警消息。

表3 丹巴县泥石流发生的降水阈值

表4 丹巴县泥石流发生的时间阈值

2.2 降雨型泥石流的阈值验证

由于数据量过大,本文随机抽取灾害样本中的一些灾害数据进行验证,结果见表5。通过丹巴县的部分泥石流数据作阈值检验,灾害发生的等级预报符合所作阈值范围,阈值预警准确率较高,整体准确率超过90%。由于丹巴县地理位置特殊,等级达到二级时就需要作相应预报。但在实际生活生产中,若所有等级为二时都作预报,那么空报的可能性较高,漏报可能性较低。但随着数据的不断收集增加,阈值也将会在今后的泥石流灾害预报中进行检验和订正。

2.3 降雨预测分析

本研究将主要针对5—8月的降雨进行预测分析, 实验数据分为两个子集——训练集和测试集。 LSTM作为循环神经网络的一种,若训练数据时间周期太长, 也会遗忘先前学到的数据规律, 因此对于模型训练的数据集时间跨度不宜太长, 但数据太少模型也不能训练出好的结果, 因此, 本实验决定采用近10年的数据进行模型的训练。训练数据集为2010—2017年记录的共4 700个数据, 占总数据记录的80%。测试数据集为2018—2019年的1 180条数据记录, 占总数据的20%。表6为模型对丹巴县5—8月的降雨量预测误差结果, 分别是平均绝对误差(MAE)和均方误差(MSE), 误差结果均低于1.5 mm, 说明了模型是切实可行的。图3、表6为丹巴县2019年5—8月日累计降雨量预测情况, 整体预测效果良好, 预测结果和实际数值非常接近, 但其中5月中下旬和8月上旬, 预测结果出现了较大的偏差, 可能的原因是高原气候的多变导致降雨量出现波动, 致使模型没有完全学习到数据的变化规律。

2.4 降雨型泥石流预警方法

确定了泥石流发生时的降雨阈值和时间阈值后, 再结合24 h累计降雨量的预测, 可对未来的泥石流发生情况进行及时的预警预报, 提前发布预警信息。预警方法如下:

(1)将前3日的24 h累计降雨量数据输入模型, 通过计算可以得到未来几日的24 h累计降雨预测值。

(2)将降雨预测结果与阈值进行比对, 并考虑降雨发生的时间, 可以得出预警等级的大小及泥石流发生可能性。

表5 丹巴县部分泥石流数据的阈值检验

表6 丹巴县5—8月降雨预测结果误差

图3 丹巴县2019年5—8月降雨预测结果

3 结 论

采用LSTM方法预测短时降雨量,并统计了近10年泥石流数据，大致划定了预警阈值区间,对四川省丹巴县气象站2010—2019年日累计降雨量进行分析计算,结论如下:

(1)通过统计近10年所发生的泥石流灾害情况,采用统计分类的方法划定了预警阈值,划分为降雨阈值和时间阈值,并给出预警等级和发生可能性大小,阈值预警准确率超过90%。

(2)整体模型降雨量预测误差均低于1.5 mm,5—8月各月预测效果良好,但5月下旬和8月上旬的预测出现较大误差,可能是在汛期的开始和结尾时期，高原气候不稳定而出现降雨波动,致使模型没有完全学习到数据的变化规律。

(3)结合本研究的降雨阈值结果和降雨预测方法,降低了传统气象预警的复杂度,实现气象预警一体化,即“预警=阈值+预测”,能对提前发布预警信息提供较强的指导意义。