超大直径盾构在海域软土地层掘进推进系统参数控制方法研究
——以汕头海湾隧道工程为例
2020-03-09孙振川王超峰杨将晓王发民
陈 桥, 孙振川, 张 兵, 王超峰, 杨将晓, 王发民
(1. 盾构及掘进技术国家重点实验室, 河南 郑州 450001; 2. 中铁隧道局集团有限公司, 广东 广州 511458; 3. 汕头市苏埃通道建设投资发展有限公司, 广东 汕头 515000)
0 引言
推进系统是盾构的重要组成部分,既为盾构提供推力以克服掘进时的破岩力、摩擦阻力、土舱/泥水舱压力等,也用于盾构姿态控制,以确保盾构按照隧道设计轴线掘进。直径6 m级的中型盾构,其推进系统一般有4个或5个分区; 12 m以上超大直径盾构,其推进系统一般有6个分区。随着分区数量的增加,各个分区压力分配方式的可选择性也增加,制定分区压力分配方案的难度也增加。此外,由于主机质量大,尤其是刀盘、主轴承、减速机等超大、超重结构件布置集中,软弱地层承载能力差,超大直径泥水盾构(直径12 m以上)[1]在软土地层“栽头”掘进的趋势比中小直径盾构更强烈。为避免盾构“栽头”掘进,需要调整推进系统分区压力,使分区之间的压力差产生的力矩能够平衡盾构主机自重的力矩。但是分区压力差过大将会造成管片环结构受力不均,使管片结构部分区域应力集中而产生裂纹、崩角,给隧道结构带来不利的影响。如何选取合适的分区压力,既能满足盾构姿态控制需求,也能改善管片结构受力状态,避免应力集中,是超大直径泥水盾构在软弱地层掘进时面临的重要难题。
在盾构姿态控制及盾构推进系统设计研究方面,文献[2]以内蒙古新街台格庙煤矿斜井工程为背景,研究了隧道设计坡角变化对栽头调整能力的影响,认为随着下坡角度不断增大,推进系统的栽头调整能力的上下限不断下降,盾构下滑力的迅速增长是造成推进系统栽头调整能力不断下降的主要原因;文献[3]研究了盾构推进过程中盾构姿态控制的关键因素,认为盾构推进过程中切口始终处于不断调整之中,并建立了推力油缸行程差和盾构切口竖向偏差量之间的对应关系,结合工程进行了验证;文献[4]研究了盾构目标位姿和盾构推进系统各分区液压缸目标运动特性,得到了盾构目标位姿与盾构各推进液压缸目标(角)位移、(角)速度和(角)加速度之间的数学解析关系,提出了根据隧道设计轴线参数方程求解盾构目标位姿和各分区推进液压缸目标运动特性的方法; 文献[5]研究了盾构推进液压系统的管道特性及管道结构参数对推进缸位移动态性能的影响,认为管道长度与管道直径是影响推进缸位移与盾构纠偏距离的关键因素,管道越长、管道直径越小,管道特性在推进缸位移上的体现越明显;文献[6]结合煤矿斜井双模式盾构,分析不同掘进模式和工况下推进油缸布局优化条件,根据单个管片受力均匀、管片环整体受力平衡及各分区推力均方差最小的优化原则,提出了推进油缸的位置及分区优化方法;文献[7]结合盾构隧道工程分析了盾构姿态控制对管片错台的影响,并提出了相应的预防措施;文献[8]基于力均方差最小和相对偏差最小的原则,研究了盾构推进系统液压缸优化布局方法;文献[9-11]重点研究了推进系统控制原理及改进设计方法;文献[12-13]从不同角度研究了盾构推进系统性能定量分析和评价方法;文献[14-15]研究了推进系统分区布置方法;文献[16]研究了盾构推进系统总推力计算方法。
综上所述,既有研究内容还存在以下不足之处:1)虽有涉及大坡度下盾构姿态控制,但是属于煤矿斜井施工领域,其坡度控制指标与公路、铁路隧道不同;2)研究对象均为中小直径盾构,尚未涉及超大直径泥水盾构姿态控制与推进系统参数选取;3)单个管片受力均匀、管片环整体受力平衡及各分区推力均方差最小的优化原则与超大直径泥水盾构姿态控制需求如何统筹协调,需要结合具体工程进行研究。本文结合汕头海湾隧道工程,研究公路隧道设计标准下,超大直径盾构姿态控制与推进系统分区压力分配、管片结构受力的关系,提出相应的参数控制方法,以达到盾构姿态控制需求和改善管片结构受力的目的。
1 工程概况
汕头海湾隧道工程盾构段全长3 048 m,分为东、西两线,分别采用2台15 m级超大直径泥水盾构施工,工程按照一级公路等级设计,盾构段依次采用-2.9%、-0.3%、0.3%、3.0%的“V”形纵坡形式。汕头海湾隧道工程地质纵断面如图1所示,盾构施工段将要穿越的地层有: 填筑土、淤泥、淤泥质土、淤泥混砂、粉细砂、粉质黏土、中砂、粗砂、砾砂、砾质黏性土,微弱中全风化花岗岩等。此外,工程不良地质有砂土液化、软土震陷、花岗岩球状风化体、基岩突起、有害气体等。地勘显示盾构在掘进过程中遇到顶部为淤泥混砂、淤泥,洞身掘进段为泥质混砂、中粗砂、粉质黏土、淤泥质土、砾质黏性土,底部为中粗砂、淤泥质土、砾质黏性土,该工程整条线路上此类土体的累计长度约为2 007.5 km,占总掘进长度的65.90%。本文研究的盾构掘进区间地层土体物理力学参数见表1。
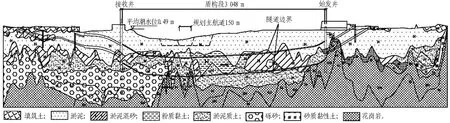
图1 汕头海湾隧道工程地质纵断面图

表1 主要土体物理力学参数
2 盾构主机掘进时的受力分析
2.1 坡度对盾构主机倾覆力矩的影响
盾构主机总质量约2 751 t,不同坡度下的主机总质量相对于其几何中心的倾覆力矩见表2。从水平放置到最大坡度时,主机倾覆力矩变化幅度为0.045%,由此可见其对盾构主机重心的偏心力矩影响非常小。
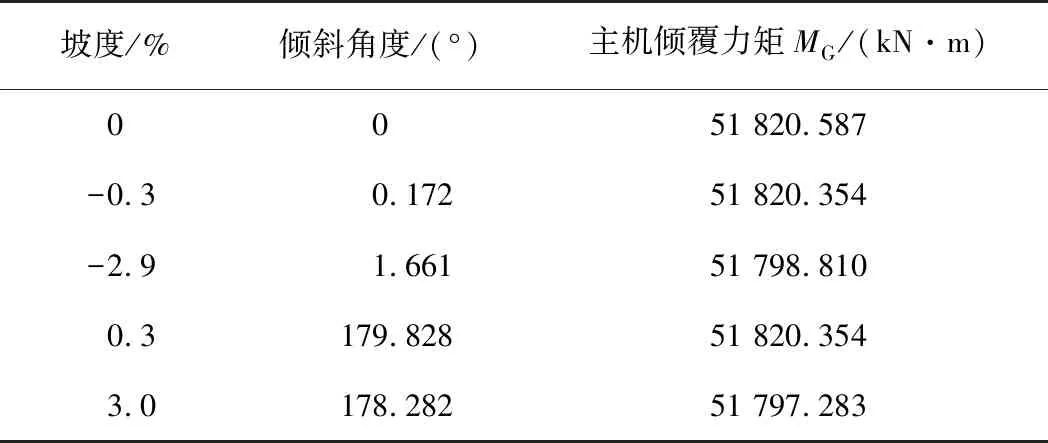
表2 不同坡度下的盾构主机倾覆力矩
2.2 盾构主机受力平衡方程
盾构掘进时,所受外力的分布、大小、方向比较复杂,在分析其受力时,需要进行等效处理。当盾构在沿直线掘进时,若将盾构主机作为一个整体,其受力情况如图 2所示。作用在盾构主机上的力主要有: 1)重力,可等效为作用在重心处的集中力,在隧道纵向剖面上,竖直向下; 2)摩擦力,环形分布于盾体、刀盘周边上,可等效为通过盾构中心的集中力,与盾构掘进方向相反; 3)掘进阻力,包括梯度分布的泥水压力作用在刀盘及泥水舱隔板上形成的泥水阻力和盾构刀具贯入土体时的阻力,可等效为通过盾构中心的集中力,与盾构掘进方向相反; 4)总推力,为推进系统油缸作用在管片环上形成的反作用力,沿盾构掘进方向,其大小由推进系统各个分区油缸推力累加而成; 5)竖向水土压力合力,该力为均匀分布力,即图2示出的p1,可等效为通过盾构几何中心的集中力; 6)隧道地基反力,即图2示出的pg,该力为均匀分布力,可等效为通过盾构几何中心的集中力; 7)侧向水土压力,即图2示出的p2,该力为梯度分布力,可等效为通过盾构水平中心的集中力。
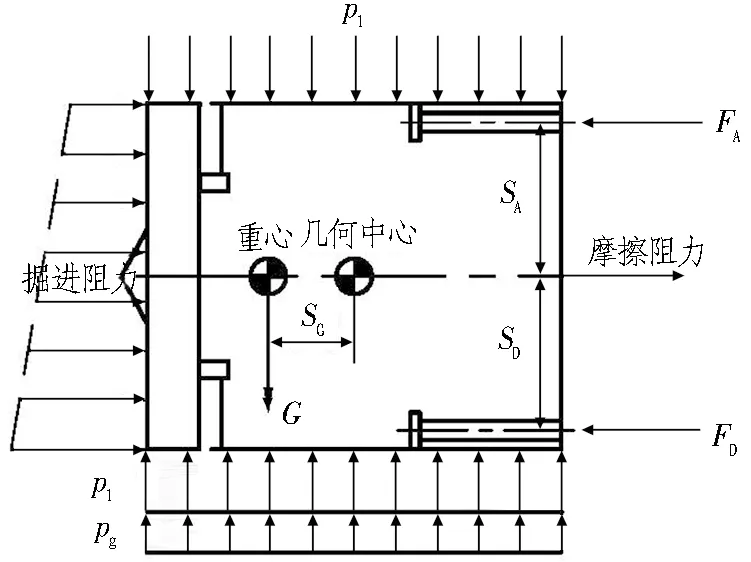
(a) 隧道纵断面盾构主机受力简图
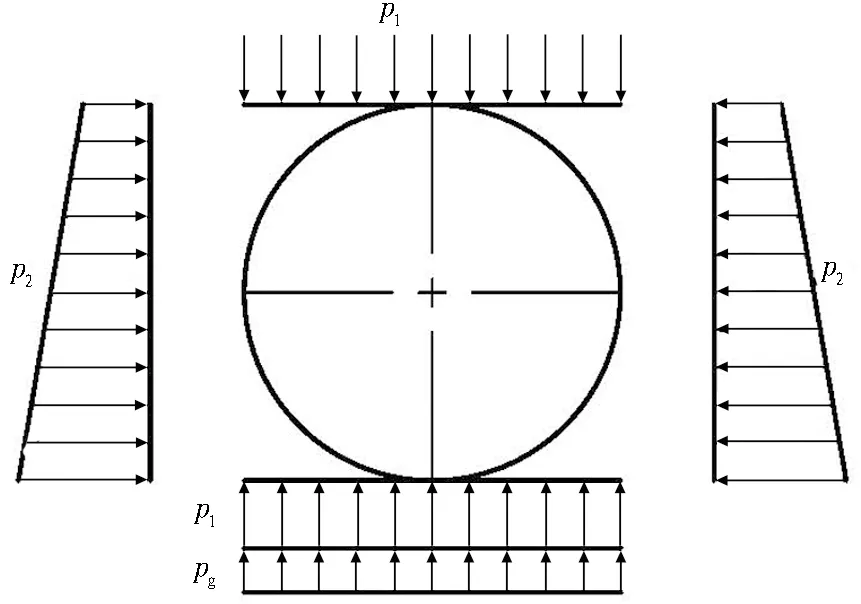
(b) 隧道横断面盾构主机受力简图
盾构掘进时的姿态主要由推进系统来控制,通过控制不同分区油缸之间的推力,使盾构姿态保持稳定并沿着隧道设计轴线掘进。由于盾构刀盘、主轴承、驱动电机、减速箱等大质量零部件密集分布在几何中心前方,造成其重心与其几何中心并不重合,即重力在竖直平面上形成力矩,导致盾构在掘进时有“栽头”的趋势。由图2可知,盾构所受的掘进阻力、摩擦阻力和隧道地基反力等效后均通过盾构几何中心,在竖直平面上的力矩为0 kN·m。由于盾构为圆形结构,竖向和侧向的水土压力大小相等、方向相反,故可认为其相互抵消。综合上述分析,假设盾构沿直线掘进时,隧道纵向剖面两侧的分区推力相等,即分区B与分区F、分区C与分区E之间的推力相等,纵向剖面上分区B推力形成的力矩与分区C推力形成的力矩相等,则重力形成的力矩将与推进系统分区A、D推力差形成的力矩来平衡。根据平面力系平衡的条件,得到盾构沿直线掘进时各个分区的推力和力矩关系如式(1)所示,盾构推进系统分区及相关参数取值分别如图3和表3所示。
(1)
式中:FA为分区A油缸总推力, kN;SA为分区A油缸推力与水平中心距离, mm;FB为分区B油缸总推力, kN;SB为分区B油缸推力与水平中心距离, mm;MG为盾构主机倾覆力矩, kN·m;G为盾构主机重力,kN;FC为分区C油缸总推力, kN;SC为分区C油缸推力与水平中心距离, mm;FF为分区F油缸总推力, kN;F总为推进系统总推力,kN;FD为分区D油缸总推力, kN;SD为分区D油缸推力与水平中心距离, mm;FE为分区E油缸总推力, kN;pB为分区B油缸压力, MPa;nB为分区B油缸数量;MH为等效掘进阻力矩, kN·m;MI为等效摩擦力矩, kN·m;SG为主机重心与几何中心距离, m;θ为盾构始发时中心线与水平线之间的角度,(°);D为推进系统油缸无杆腔内径,mm。
转换后得到如下关系:
(2)
(3)
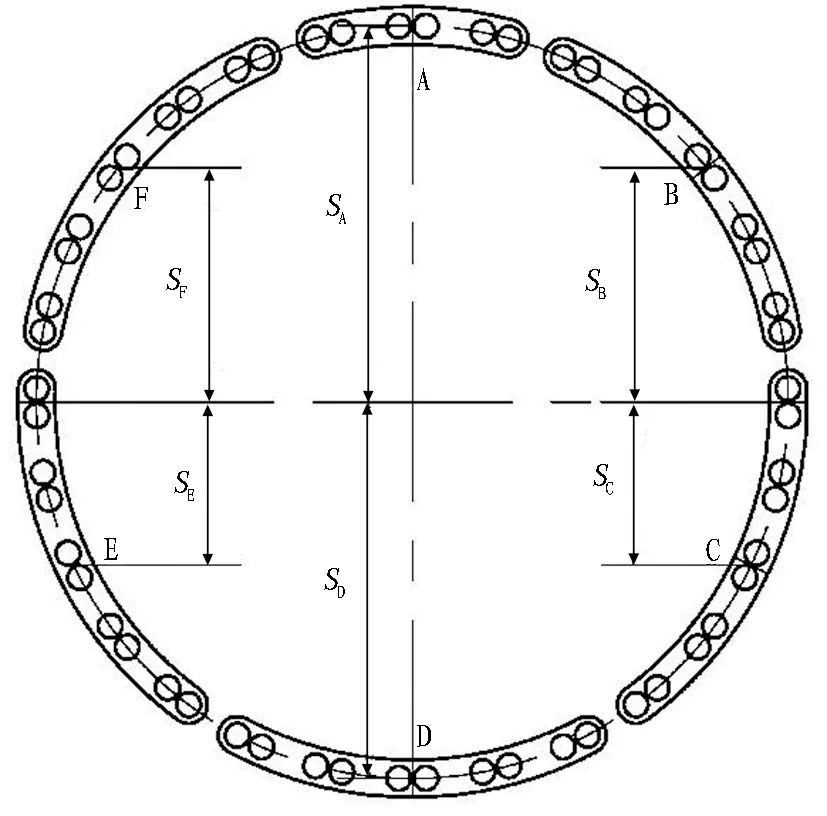
图3 推进系统油缸分区及分区力臂
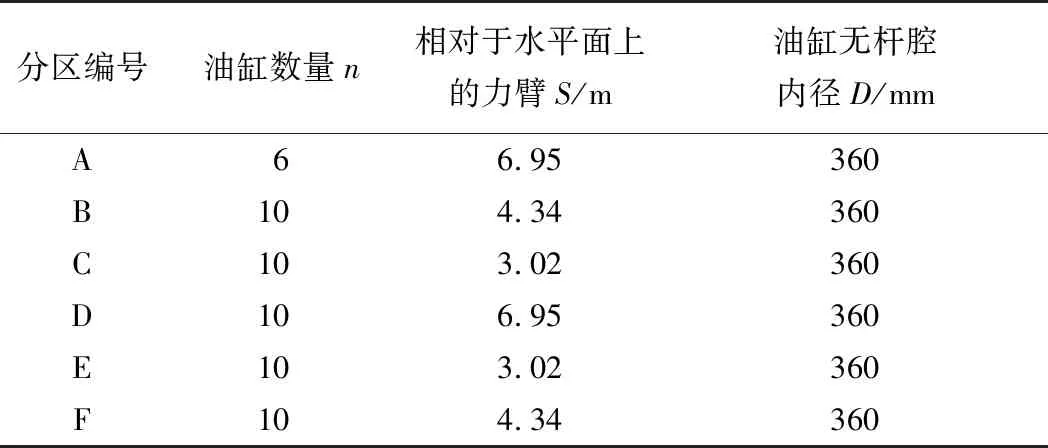
表3 推进系统分区油缸参数
3 各分区油缸压力及推力变化规律
盾构在试掘进阶段,总推力计划控制在50 000 kN左右,根据式(2)、式(3)和表 3中的参数,在总推力为50 000 kN时,分区B油缸压力和其他分区压力(A、C、D)关系如图 4所示(分区B与分区F相同,分区C与分区E相同,故不重复绘制)。由图4可知,在维持总推力为50 000 kN不变,考虑所用盾构液压系统最大工作压力为35.0 MPa的条件下,分区B油缸压力工作范围为0.0~7.5 MPa,在此范围内,随着分区B油缸压力的增加,分区C压力增加,分区D和分区A的压力逐渐减小,且分区A压力减小的速度更快。当分区B压力pB满足条件0 MPa
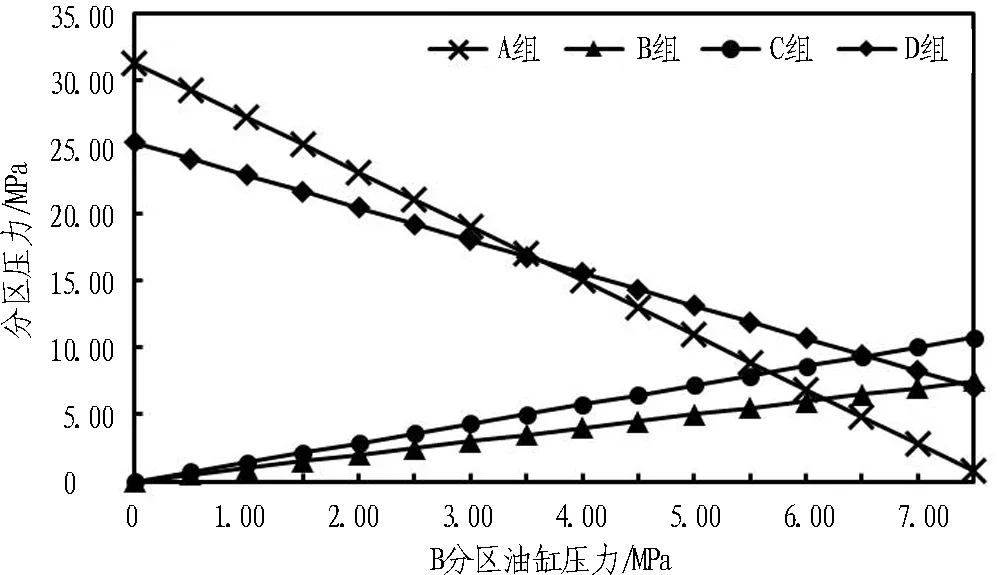
图4 分区B油缸压力和其他分区压力变化关系图
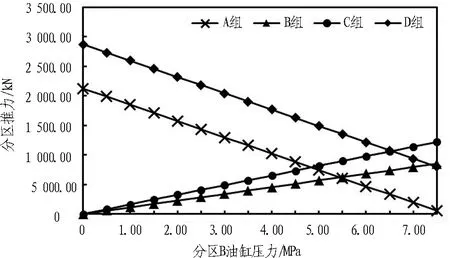
图5 分区B油缸压力和其他分区推力关系图
4 推进系统分区最优推力选取
由表4可知,在保证盾构掘进姿态和总推力一定的前提下,推进系统各个分区压力有多种不同的选取方案,但是选取不同的推力控制方案将会给管片及推进系统造成不同的影响。例如,表 4中的方案1,分区B、C、E、F推力为0 kN,即盾构掘进推力仅仅依靠分区A、D来输出,虽然该方案也能满足盾构掘进姿态控制需求,分区中的油缸压力也未超过液压系统最大工作压力,但是这种控制方案并不合理,其缺点一是未充分发挥其他4个分区的作用,二是推力集中作用在上下管片的端面,造成管片受力不均,易引起管片局部过载而破损。因此,最优的盾构推进系统分区推力选取方案应满足以下条件: 1)满足盾构总推力控制需求(间接控制推进速度); 2)满足盾构掘进姿态控制需求,避免盾构主机出现“栽头”等异常姿态; 3)在满足上述条件的前提下,推进系统各个分区推力宜分布均匀,以避免管片结构受力不均而损坏。
表4中的推力设置方案已满足上述前2个条件,因此如何选取合适的推力避免管片结构受损成为关键。从图 5中各个分区推力变化趋势来看,当分区B油缸压力pB增加时,各个分区推力分布范围有减小的趋势,即分区推力之间的差值越来越小,分布越来越均匀,故采用分区推力标准差来量化推力之间的差值,以获取最均匀的推力方案。
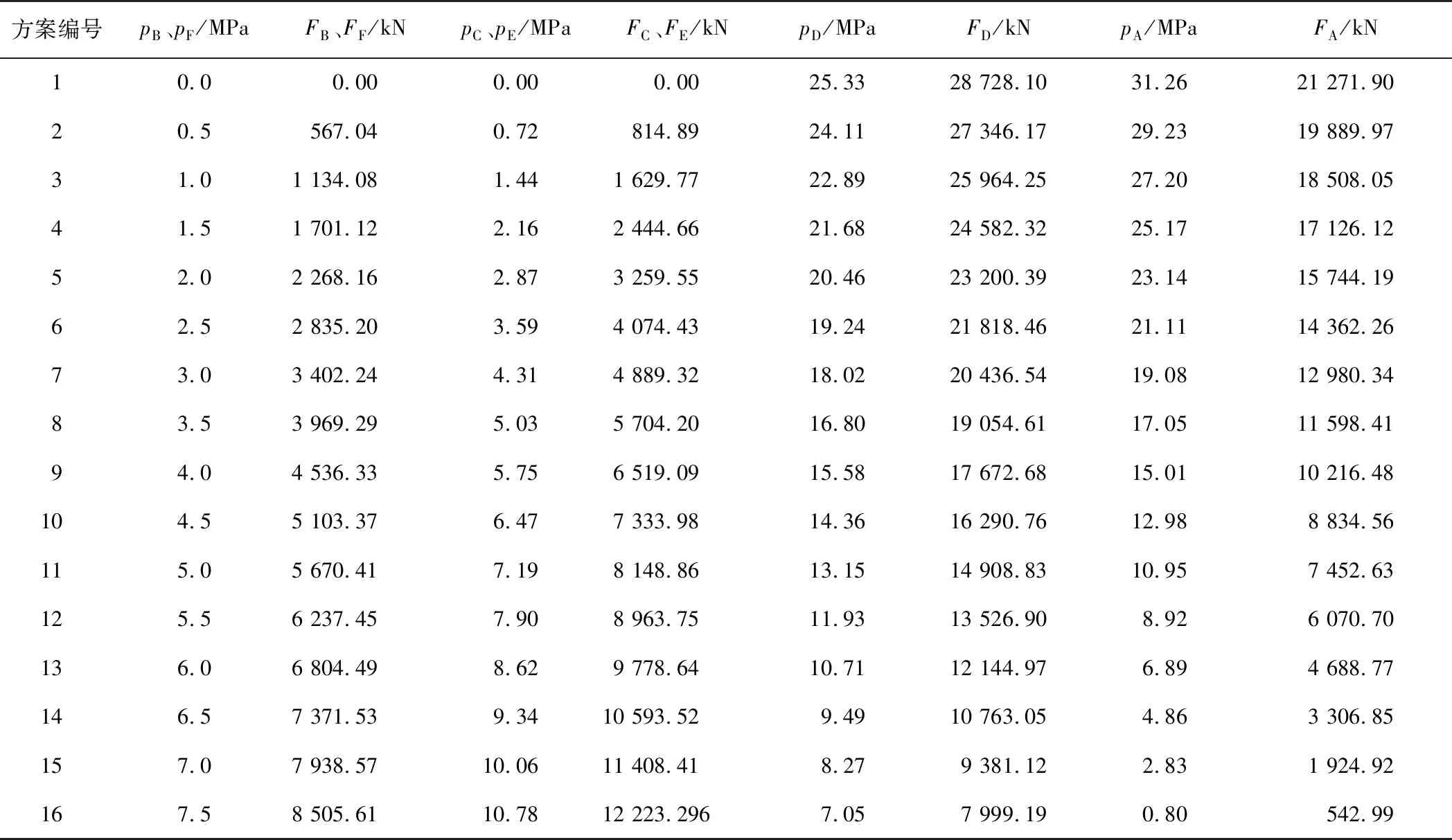
表4 各分区压力及推力参考取值
4.1 各个分区推力离散性分析
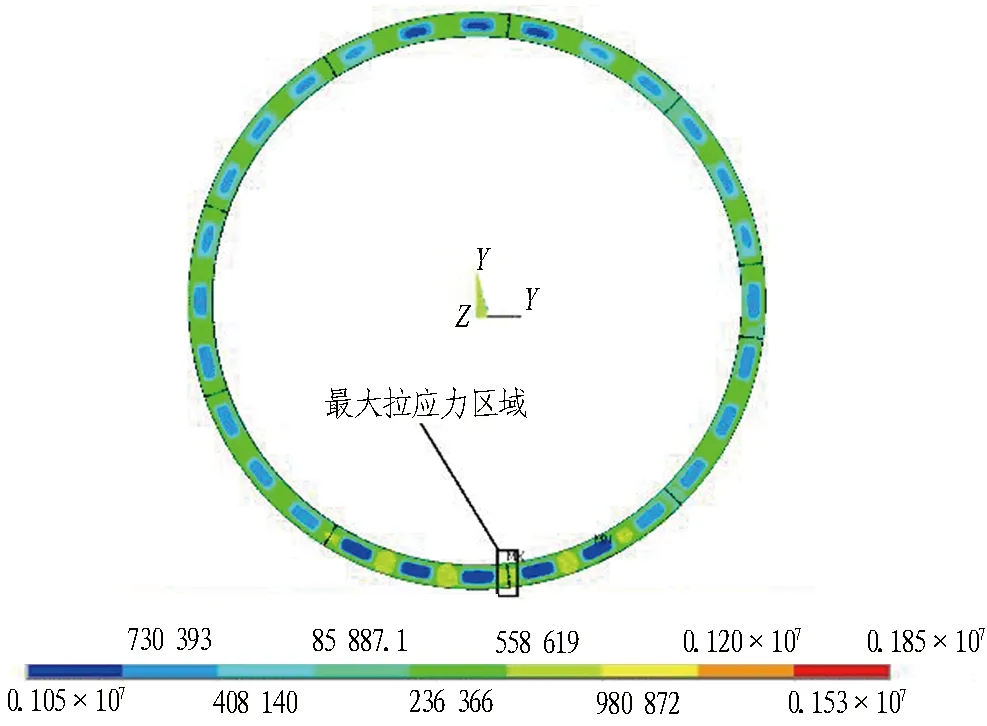
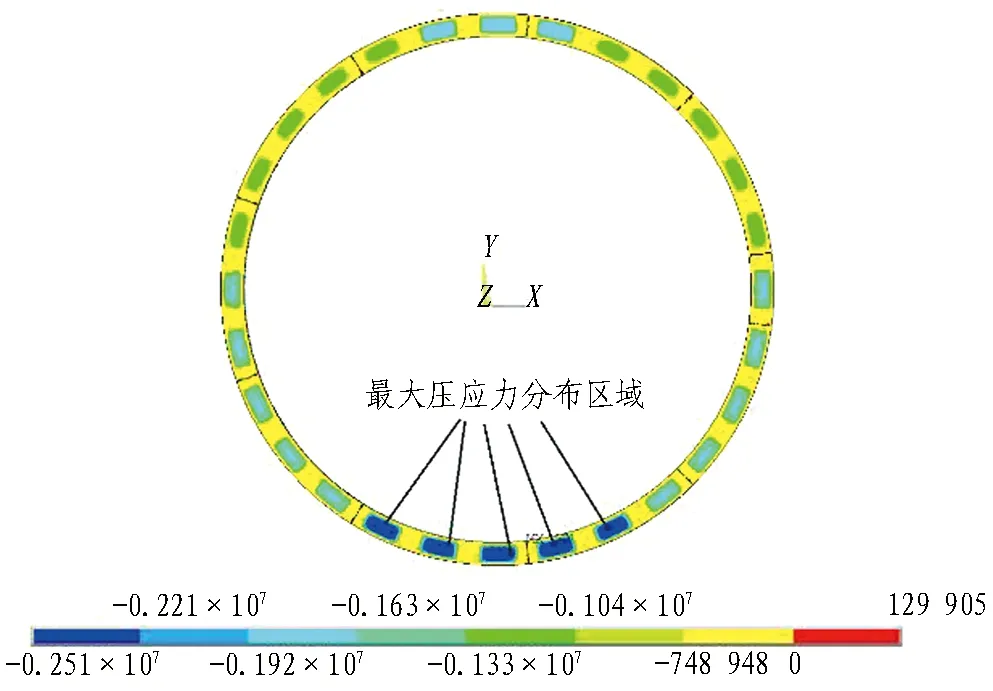
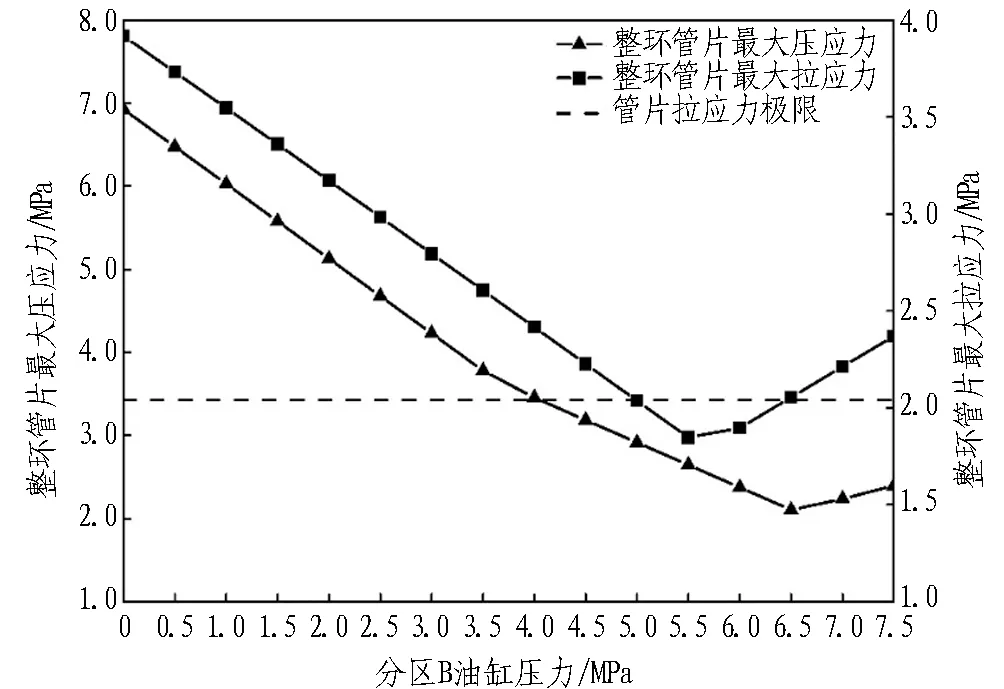
根据表4得到分区B油缸压力与各个分区推力标准差之间的关系曲线如图 6所示。由图6可知,随着分区B油缸压力pB的增加,各分区推力的标准差先逐渐减小后逐渐增加; 当pB=6.0 MPa时,各分区推力的标准差最小,随着pB的增加,各分区推力的标准差又逐渐增大。该变化趋势说明当pB=6.0 MPa时,推进系统总推力既能达到设定值50 000 kN,同时各个分区推力离散程度最低,可使管片环受力最均匀,避免管片局部受力过大可能造成的破损风险; 此外,各分区压力排序为B、F 图6 B分区油缸压力与各分区推力标准差关系曲线 上述结论是根据理论计算的结果推导出来的,还需要采用数值分析的方法分析在表 4中推力设置情况下的管片结构受力,以对最优的盾构推进系统分区推力选取方案进行验证。pB=5.5 MPa(表 4中的方案12)对应的各个分区压力作用下管片应力分布情况如图 7所示。由图7可知,管片最大拉应力为1.85 MPa,位于管片环最下端的2块管片接合面处,接合面上有管片密封垫槽和凹凸榫结构,这些结构的边缘位置拉应力较高,是容易出现崩角、破损的位置;管片环主要承受压应力,其最大压应力为2.64 MPa,位于管片环最下端的2块管片端面上,该区域为推进油缸撑靴的作用区。 (a) 管片拉应力分布 (c) 管片压应力分布 依此类推,分别计算表4中其他推力分配方案下的管片结构受力,汇总计算结果获得管片应力变化趋势如图 8所示。由图8可知,随着分区B油缸压力的增大,整环管片最大拉应力和最大压应力均呈现先减小后逐渐增大的趋势,且pB=0 MPa时,整环管片最大压应力和最大拉应力均为最大值,但是二者也有各自的特点: 当0 MPa 图8 不同分区推力下管片结构受力变化趋势 当0 MPa GB 50010—2010《混凝土结构设计规范》[17]中规定的C60混凝土轴心抗压强度设计值为27.5 MPa,轴心抗拉强度设计值为2.04 MPa。因此,当0 MPa 1)确定推进系统分区工作压力时,既要满足盾构姿态的控制需求,也要满足管片结构的受力需求,且后者的要求更加严格。 2)在满足盾构姿态可控的前提下,减小推进系统各个分区推力的离散性,使整环管片受力尽可能均匀,可改善整环管片的受力状态。 3)当总推力为50 000 kN时,图 3所示的推进系统布局中,各个分区油缸压力按照表 4中的方案12确定是最优的,可缓解管片应力集中,降低管片出现崩角、破损的概率。 4)盾构总推力一定时,推进系统各个分区存在合适的压力控制范围,在满足盾构姿态控制需求的前提下,使管片结构受力满足设计规范,利用该方法可确定不同总推力下分区油缸压力最优分配方案。 5)盾构在掘进过程中其受力状态是动态变化的,提出的盾构力学平衡方程是对盾构受力状态的一种近似描述,存在一定的误差。下一步需要将本文所述的控制方法在工程实践中进行检验与优化。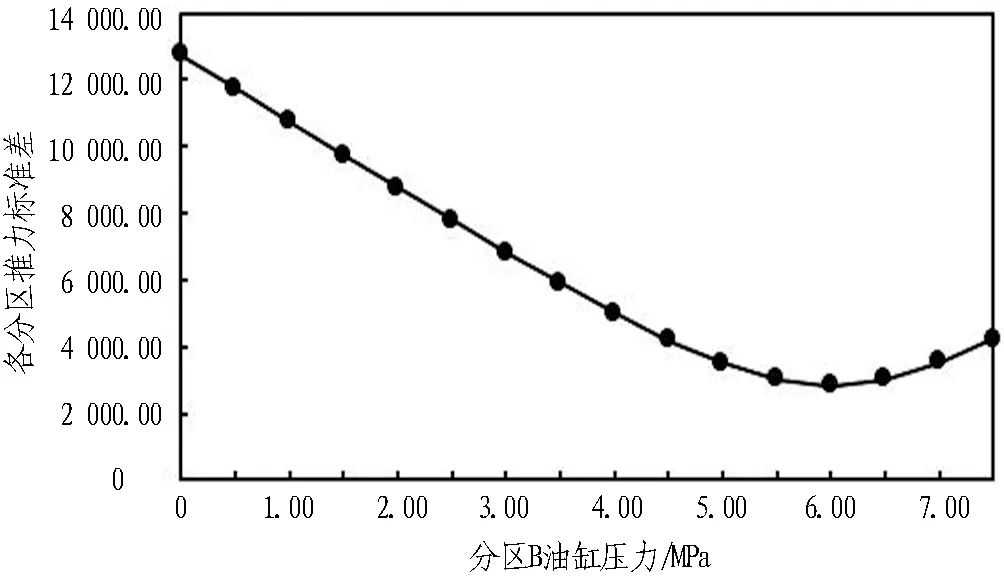
4.2 不同分区推力下的管片结构受力
5 结论与讨论
