Interfacial Stress Analysis on Skutterudite-based Thermoelectric Joints under Service Conditions

2020-03-09SHAOXiaoLIURuiHengWANGLiangCHUJingBAIGuangHuiBAIShengQiangGUMingZHANGLiNaMAWeiCHENLiDong

无机材料学报 2020年2期

SHAO Xiao, LIU Rui-Heng, WANG Liang, CHU Jing, BAI Guang-Hui, BAI Sheng-Qiang, GU Ming, ZHANG Li-Na, MA Wei, CHEN Li-Dong

SHAO Xiao1,2, LIU Rui-Heng1,3, WANG Liang1, CHU Jing1,2, BAI Guang-Hui4, BAI Sheng-Qiang1,3, GU Ming1, ZHANG Li-Na4, MA Wei4, CHEN Li-Dong1,3

(1. The State Key Lab of High Performance Ceramics and Superfine Microstructure, Shanghai Institute of Ceramics, Chinese Academy of Sciences, Shanghai 201899, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China; 3. Center of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, China; 4. Science and Technology on Space Physics Laboratory, Beijing 100076, China)

In thermoelectric (TE) devices, the interfacial reliability greatly influenced devices’ durability and power output. For skutterudites (SKD) devices, TE legs and electrodes are bonded together with diffusion barrier layer (DBL). At elevated temperatures, DBL react with SKD matrix or electrode to generate complex interfacial microstructures, which often accompanies evolutions of the thermal, electrical and mechanical properties at the interfaces. In this work, a finite element model containing the interfacial microstructure characteristics based on the experimental results was built to analyze the interfacial stress state in the skutterudite-based TE joints. A single-layer model was applied to screen out the most important parameters of the coefficient of thermal expansion () and the modulus of DBL on the first principle stress. The multilayer model considering the interfacial microstructures evolution was built to quantitively simulate the stress state of the TE joints at different aging temperatures and time. The simulation results show that the reactive CoSb2layer is the weakest layer in both SKD/Nb and SKD/Zr joints. And by prolonging the aging time, the thickness of the reaction layer continuously increased, leading to a significant raising of the interfacial stress. The tensile testing results of the SKD/Nb joints match the simulation results well, consolidating accuracy and feasibility of this multilayer model. This study provides an important guidance on the design of DBL to improve the TE joints’ mechanical reliability, and a common method to precisely simulate the stress condition in other coating systems.

thermoelectric joints; diffusion barrier layer; finite element model; tensile strength

Thermoelectric (TE) technology has attracted great attention because it can convert heat into electric power directly with the advantages of no moving parts and long durability, especially for the applications in deep space exploration, waste heat recovery, and other special fields[1-3]. Over the past several decades, many high-performance TE materials and devices were developed[4-8], providing great opportunities for large-scale application of TE power generation. Among them, skutterudite-based (SKD) devices exhibited very high conversion efficiencies up to 12%[9], making SKD one of the most potential candidates for the practical applications.

As the SKD device steps forward to industrial application from laboratory[10], the mechanical reliability becomes the top concern since TE devices often work under harsh service conditions, such as high temperature difference, mechanical vibration with wide frequency, extremely long service time. A TE device comprises of n-, p-type TE legs and electrodes as major components. Previously, researchers paid a lot of attention to the mechanical property of SKD materials themselves[11-13], and demonstrated that the SKD materials exhibit excellent mechanical performance to bear service stress[14-15]. However, at the electrode interface, the Sb elements of skutterudites matrix diffused into electrode materials such as Cu, Ni, and Mo[16-17]or diffusion barrier layer (DBL) such as Ti, Mo, Mo-Ti, Cr80Si20, Nb, Ti100-xAl(= 3–12)[18-23]during the long-time service at high temperatures. The elemental diffusions and chemical reactions at the interface not only result in dramatical increase of the interfacial electrical and thermal resistivity[24], but also induce the mechanical injury or disability.

Numerical analysis for residual interfacial stress in multilayer system was well studied in the past decades. It was recognized that the coefficient of thermal expansion () of the component layers plays a critical role on interfacial reliability[25]. Interface morphology should also affect interface stability in multilayer systems like thermal barrier coatings[26]. Li,[27]found that the thermal stress in segmented CoSb3/Bi2Te3device could be reduced by introducing a graded layer between CoSb3and copper electrode. However, all above researches treated multilayer systems as inert (without compositional or structural change) at high temperature. Actually, in TE joints, element diffusion and reaction are inevitable during whole service life. Therefore, the interfacial compositions and microstructures would continuously evolve, which influence the interfacial mechanical behavior unexpectedly.

This study reports a numerical analysis model based on finite element simulation method to investigate the dynamic interfacial stress at the SKD/DBL joint by taking the microstructure evolution into account. A single- layer model was established, and the interfacial stress in the TE joints with different DBL was calculated. Based on the experimental results on the interface observation and properties measuring of reaction layers, a multilayer model considering microstructure evolution was built to quantitively simulate the stress state of the aged TE joints. The tensile test results of SKD/Nb joints matched well with the simulation results.

1 Finite element model and experimental procedure

1.1 Governing equation of thermal-structural model

A transient thermal-structural model is applied for stress in SKD/DBL joints to simulate the sintering- cooling process. Residual stress results from change of temperature and difference of material properties. For cooling period, the transient thermal conducting equation can be derived according to energy conservation law:

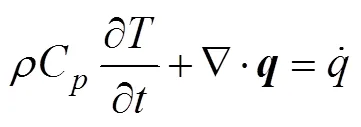
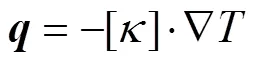
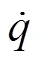
Once temperature decreases, the difference betweenof SKD and Nb causes displacement, which can be converted to strain, and then results in stress according to generalized Hooke’s law. Thus the thermal-structural governing equation can be expressed as[28]:

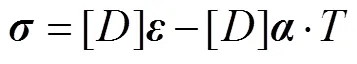
Whereandare stress and strain vectors respectively, [] is stiffness matrix,isvector, Δis the difference between present temperature and reference temperature (0). Finally, the stress distribution can be figured out.

For a certain site in materials, stress tensor can be divided to three principle stresses:1,2,3, from large to small, respectively. According to the first strength theory, the maximum principle stress is the main reason for fracture, which coincides well with the fracture of brittle materials’ uniaxial tension. Therefore, the first principle stress1is chosen to evaluate stress intensity.

In initial state (=0), adjacent materials are already bonded closely to form a zero-stress state. Thus, the initial temperature (960 K) is reference temperature (0) of thermal expansion. Then in cooling process, joint’s diameter is assumed to be unchanged, meanwhile upper and lower end could move vertically. Besides, model’s round side is considered as thermal insulated. On the end side surfaces, effect of cooling is also simplified as natural convection in air, in which the heat transfer coefficient was set to be 10 W·m2·K–1.

1.2 Experimental procedures

SKD/Nb joints were fabricated and aged for tensile test. Yb0.3Co4Sb12(SKD) powders and Nb foil ((0.025± 0.015) mm) were loaded into a graphite die with a diameter of 50 mm, and then sintered by hot pressed for 90 min at 690 ℃ and 60 MPa under Ar atmosphere. Nb foil was placed between two SKD layers to form a sandwich structure. The obtained joint (50 mm×4 mm) was then cut into small cylinders (10 mm) and sealed in quartz ampules under vacuum. The sealed ampules were aged under 600 and 650 ℃ in furnace for various time, and the aged joints were denoted as “temperature-aging time”, such as 600–10 d. The tensile strength was measured by Instron-5566 universal testing system at room temperature. The microstructures of interface and fracture surface were observed by SEM (ZEISS Spura 55). The constituents of interface were measured by EDS (Oxford Instrument).

2 Results and discussion

2.1 Influence of materials properties in single- layer model

Nb, Mo, Zr, Ti were chosen as the DBL candidates for SKD[22,29]. The effect of materials properties on interfacial mechanical stability was studied by using single- layer model. Theand Young’s modulus data obtained from COMSOL database are presented in Fig. 1(a-b). The calculated1are shown in Fig. 1(c). Compared with other DBL materials, the stress intensity of SKD/Mo is extremely high, which probably results from great difference ofbetween Mo and SKD (=10.6× 10–6K–1[20]). The stress of SKD/Zr interface is the lowest (1.1 GPa), even though Zr has the larger difference ofwith SKD than that of Ti. Fig. 1(c) shows that the variation trend of interfacial stress is the same as that of Young’s modulus. It is observed that bothand Young’s modulus influence stress intensity, and large Young’s modulus induces high intensity stress. Moreover, in single-layer model, the thickness of DBL affects interfacial stress weakly. In consideration of reaction activity at high temperature[22], Nb and Zr are employed for further research.

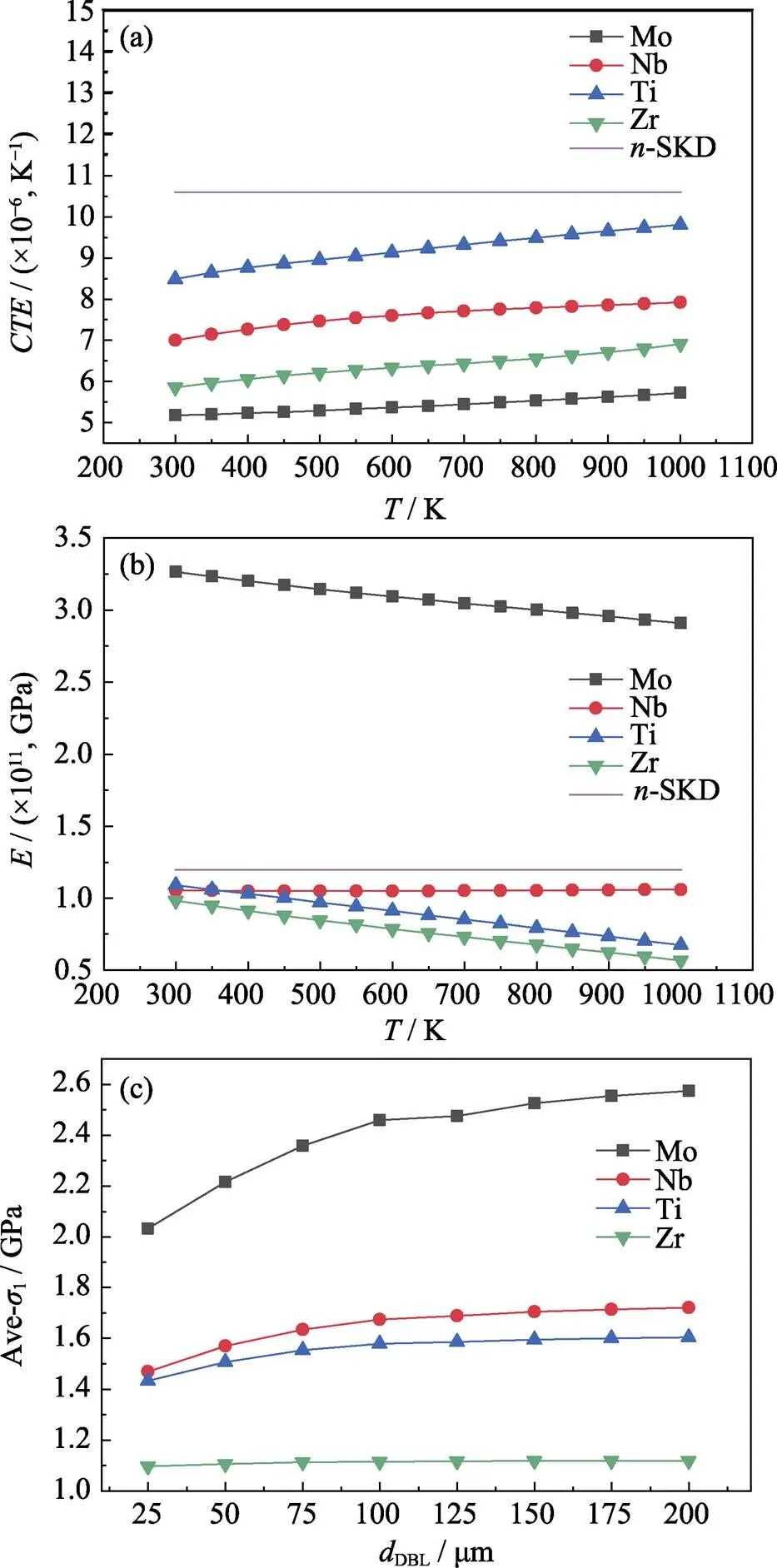
Fig. 1 (a) CTE, (b) Young’s modulus (E), and (c) variations of average first principle stresses with thicknesses of different DBL candidates (purple lines: CTE and E of SKD)

2.2 Influence of thickness of layers in multilayer model

Actually, all the SKD joints undergo the elemental diffusion and chemical reaction during long-time service at high temperature[8], which makes single-layer model inaccurate to describe the stress state of aged joints. SEM and EDS results of SKD/Nb joints after different aging time are listed in Fig. A2. No evident microcracks or micropores are observed in as-prepared joint. After aged at 600 ℃ for 5 d, NbSb2and CoSb2are detected, and micropores appear in the CoSb2layer. The thickness of NbSb2slightly increase with the increase of aging time (Fig. A2(b-d)), indicating that elevating temperature and prolonging aging time significantly aggravate diffusion and reaction. The reaction process can be described as following. At the initial stage of aging, SKD didn’t react with DBL, and there are only three layers, as the single-layer model is shown in Fig. 2(a). With aging accelerating, SKD reacted with Nb to form CoSb2and NbSb2, and micropores appeared simultaneously because of the volume change. The reaction equation can be expressed in Eq. (4):

Thus, multilayer model was built to find out the influence of micropores and diffusion layers.

To simplify the modeling and calculation, there’re some requisite assumptions in the model: (1) CoSb2and NbSb2layers are assumed to be totally flat; (2) Micropores are of ellipsoid shape, in whichandsemi-major axis (and) are equal to a multiple ofsemi-major axis (); (3) Micropores locate on the interface between NbSb2and CoSb2periodically; (4) Diameter of cylindrical model is reduced; (5) Materials are seen as isotropic and completely linear-elastic; (6) Part of material properties (Table A1) is treated as constant value or simple function of temperature because of lack in experimental data. Combining materials’ molar mass and density listed in Table A1, relationships of thickness of each layer can be obtained, as shown in Table 1. Thus, total volume of micropores ought to equal the volume difference between models before and after aging. Therefore, the relationship (Eq. (5)) between average micropore size and thickness of NbSb2is listed:

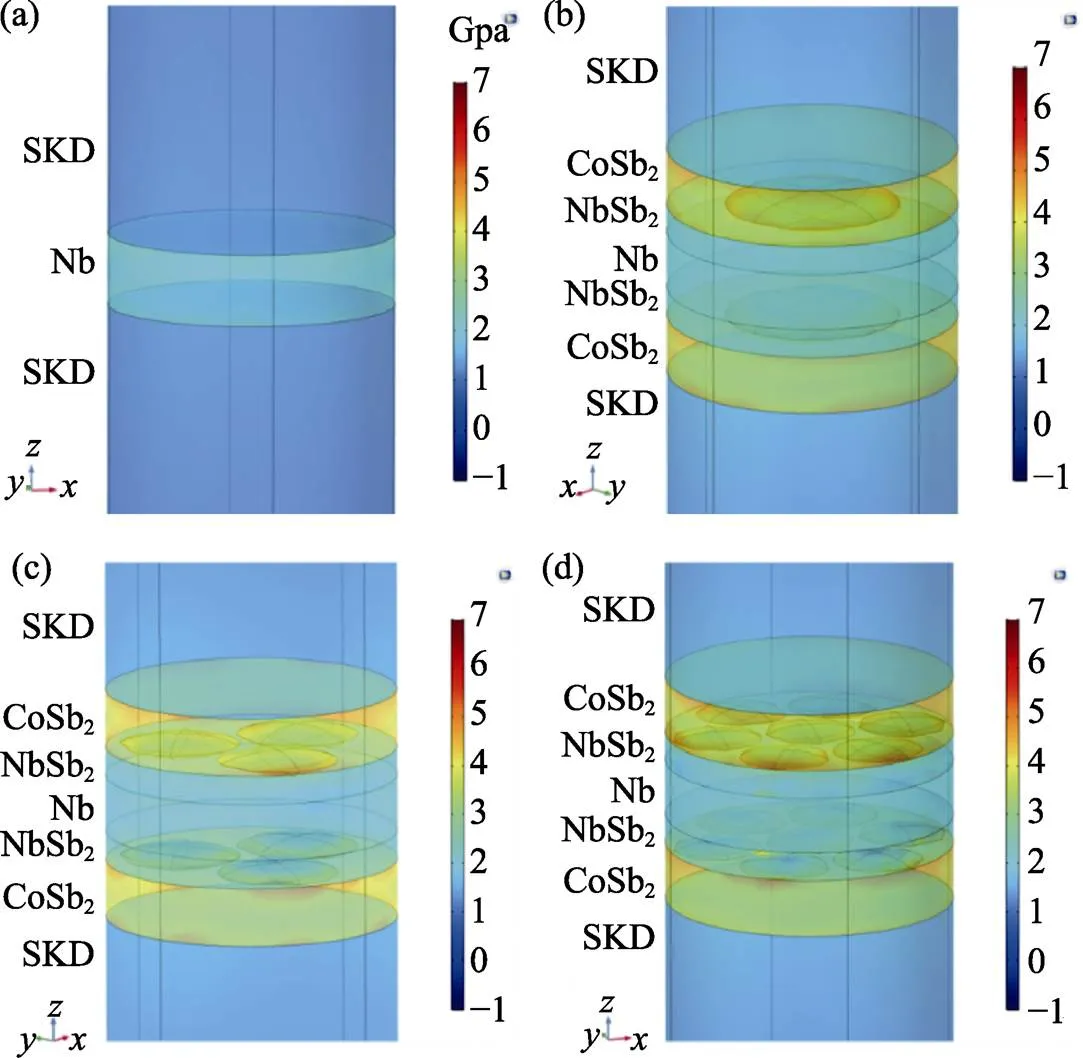
Fig. 2 σ1 distributions for (a) n=0, (b) n=1, (c) n=3, and (d) n=7 (initial thickness of Nb: 25 μm)

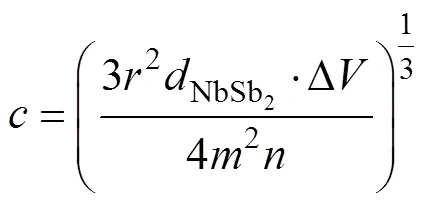
Whereis radius of model,NbSb2is thickness of NbSb2, Δis total volume of micropores,is the ratio of(or) to,is number of micropores at given total micropore volume. As long as micropores’ shape, numbers and positions are certain,NbSb2is expected to decide the extent of aging. Micropores’ positions are considered to uniformly distribute at the CoSb2/NbSb2interface. The number of microporeswas set as 1, 3, 7, and the distributions for each number are shown in Fig. 2(b-d).According to calculation results presented in Fig. A3, the ratio of(or) to() made little difference to stress distribution, which won’t be discussed in the next part.

The diffusion and reaction process of SKD/Zr joint is similar with SKD/Nb, and the reaction layer is ZrSb2[22]. It can also be analyzed by using multilayer model, and the results are shown in Fig. A4.

The evolution of the interface can be simplified descripted by 3 parameters of,DBLandNbSb2. The positions of micropores need to be set manually for each different. Whenchanges from 1 to 7, the micropore size decreases from 5.3 μm to 1.2 μm. Furthermore, to eliminate the influence of abnormal stress caused by low-quality elements mesh in much thinner barrier layer and diffusion layer, average first principle stress is applied to evaluate interfacial stress intensity. Fig. 2(a) gives the initial stress distribution of SKD/Nb interface which is the same with the single layer model. The stress concentrates on Nb layer, and the maximum principle stresses of Nb/SKD interface is 2.383 and 1.46 GPa, respectively. Fig. 2(b-d) shows the1distribution in multilayer model with different micropore numbersat the same given Δ. After aging, all stress values with increasingare much higher than the initial ones. For all cases, maximum stresses are found at the CoSb2layers. WhenNbSb2=10 μm, the maximum1are 5.83 GPa for=1 and 7.79 GPa for=7, indicating that the diffusion reaction induce large internal stress. Fig. 3 shows theDBLandNbSb2dependent1at SKD/CoSb2and CoSb2/NbSb2interfaces. The average stress of CoSb2/NbSb2interface is always the largest value for different, indicating that CoSb2/NbSb2is the most unstable interface. In Fig. 3(b, e, h), contour lines are approximately parallel toDBLaxis, which means the thickness of reactive NbSb2plays a dominate role on stress of CoSb2/NbSb2interface.

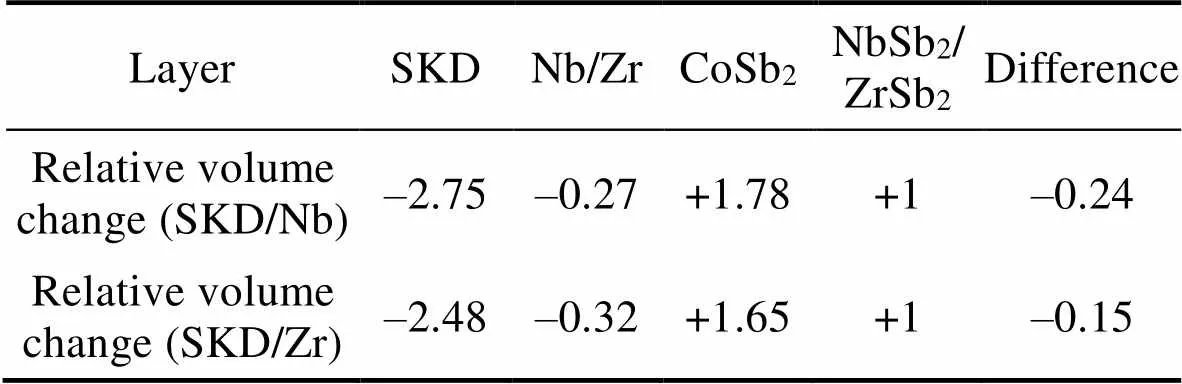
Table 1 Relative volume changes for one interface (SKD/Nb and SKD/Zr joints)

2.3 Tensile test results and validation of models

SKD/Nb joints are fabricated and aged for tensile test. After fracture, bonding strength are calculated by Eq. (6):

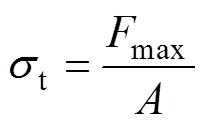
Wheretis tensile strength,maxis the maximum load,is base area of joints. The results are listed in Table 2. It is obvious that accelerated aging worsens interfacial bonding severely. With theNbSb2grows from 0 to 12 μm, the tensile strength decreases from 9.68 MPa to 1.46 MPa. The decreasing trend of tensile strength is consistent with the increasing trend of calculated stress. Furthermore, after tension, by comparing structures and compositions of the fracture surfaces, location of the weakest interface can be found. All of the aged joints break at CoSb2layer (Fig. 4(d-e)), while the unaged joints break at SKD/Nb interface (Fig. 4(a)). With elevated aging temperature or prolonged aging time, the proportions of CoSb2on fracture surface (SKD side, Fig. 4(d)) increases obviously (Table 2), indicating that the fracture locations tend to be the CoSb2/NbSb2interface. The fracture locations are completely consistent with calculation results. All of the experimental results verify the validity of above simulation model.

4 Conclusion

In this study, a single-layer model was established to calculate the interfacial stress in the TE joints with different DBL. It’s found that the DBL materials with small modulus and similarwith SKD can reduce the interfacial stress. Based on the experimental results, a multilayer model considering microstructure evolution is built to quantitively simulate the stress state of the aged TE joints. Large thickness of reaction layers and volume changes can intensify stress at interface remarkably. Both in SKD/Zr and SKD/Nb joints, the biggest first principle stress locates at CoSb2layer. Tensile test results of SKD/ Nb joints fit simulation results well, proving the feasibility of this model to simulate the stress state in multilayer system containing complex microstructures, which is helpful to design the high stability electrode interface structure for SKD TE devices.

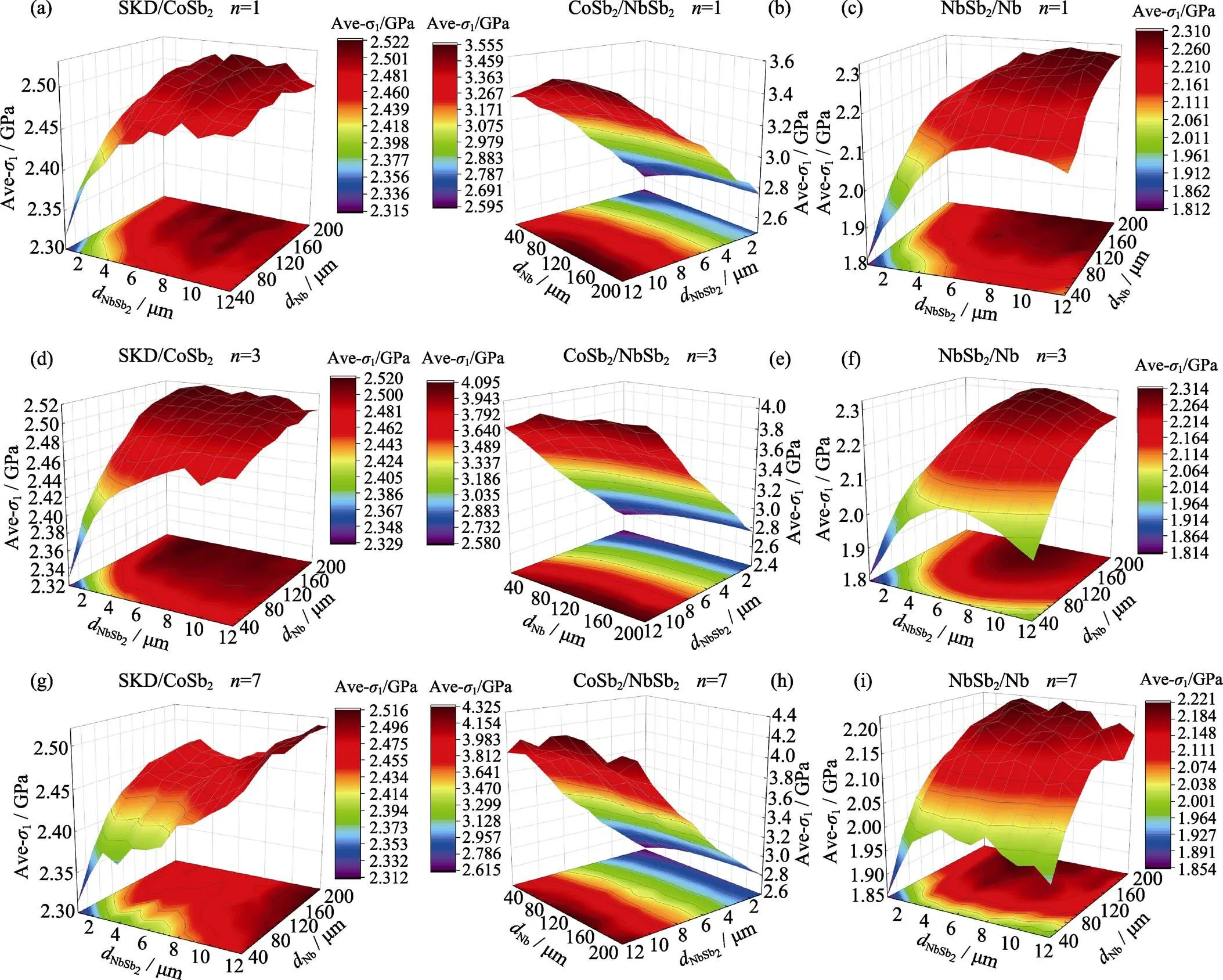
Fig. 3 Variations of average σ1 on each interface with thicknesses of NbSb2 and Nb

Fig. 4 EDS mappings of (a, d) interfaces and (b, e) fracture surfaces of (a-b) unaged joint and (d-e)sample 650-10d (White line indicating the fracture surface, and white arrow indicating direction of observation in (b) or (d)); Total element data were shown in table (c) for figure (b) and in table (f) for figure (e)

Table 2 Thicknesses of NbSb2 layer dNbSb2, average sizes of micropores c, tensile strengths σt, maximum calculated stresses Ave-σ1 and the location interfaces, compositions of tensile fracture surface for series of aging SKD/Nb joints

Supporting materials:

Supporting materials related to this article can be found at https://doi.org/10.15541/jim20190112.

[1] BELL L E. Cooling, heating, generating power and recovering waste heat with thermoelectric systems., 2008, 321(5895): 1457–1461.

[2] CHAMPIER D. Thermoelectric generators: a review of applications., 2017, 140: 167–181.

[3] CHEN L, BAI S, ZHANG Q. Technologies and applications of thermoelectric devices: current status, challenges and prospects., 2019, 34(3): 279.

[4] SALES B C, MANDRUS D, WILLIAMS R K. Filled skutterudite antimonides: a new class of thermoelectric materials., 1996, 272: 1325–1328.

[5] LIU H, SHI X, XU F,Copper ion liquid-like thermoelectrics., 2012, 11(5): 422–425.

[6] ZHAO L D, LO S H, ZHANG Y,Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals., 2014, 508(7496): 373–377.

[7] ZHANG Q H, HUANG X Y, BAI S Q,Thermoelectric devices for power generation: recent progress and future challenges., 2016, 18(2): 194–213.

[8] HE R, SCHIERNING G, NIELSCH K. Thermoelectric devices: a review of devices, architectures, and contact optimization., 2018, 3(4): 1700256.

[9] ZHANG Q, LIAO J, TANG Y,Realizing a thermoelectric conversion efficiency of 12% in bismuth telluride/skutterudite segmented modules through full-parameter optimization and energy- loss minimized integration., 2017, 10(4): 956–963.

[10] YAO Z, QIU P, LI X,Investigation on quick fabrication of n-type filled skutterudites., 2016, 31(12): 1375–1382.

[11] RAVI V, FIRDOSY S, CAILLAT T,Mechanical properties of thermoelectric skutterudites., 2008, 969: 656–662.

[12] SALVADOR J R, YANG J, SHI X,Transport and mechanical properties of Yb-filled skutterudites., 2009, 89(19): 1517–1534.

[13] DAHAL T, KIM H S, GAHLAWAT S,Transport and mechanical properties of the double-filled p-type skutterudites La0.68Ce0.22Fe4–CoSb12., 2016, 117: 13–22.

[14] RUAN Z, LIU L, ZHAI P,Residual strength degradation of CoSb3skutterudite compounds under low-cycle fatigue loading., 2012, 41(6): 1487–1492.

[15] WEN P, ZHU Y, CHEN J,The microstructure and thermoelectric properties of Yb-filled skutterudite Yb0.1Co4Sb12under cyclic thermal loading., 2016, 25(11): 4764–4768.

[16] ZHAO D, LI X, HE L,Interfacial evolution behavior and reliability evaluation of CoSb(3)/Ti/Mo-Cu thermoelectric joints during accelerated thermal aging., 2009, 477(1/2): 425–431.

[17] SHI L, HUANG X, GU M,Interfacial structure and stability in Ni/SKD/Ti/Ni skutterudite thermoelements., 2016, 285: 312–317.

[18] FAN X C, GU M, SHI X,Fabrication and reliability evaluation of Yb0.3Co4Sb12/Mo–Ti/Mo–Cu/Ni thermoelectric joints., 2015, 41(6): 7590–7595.

[19] WOJCIECHOWSKI K T, ZYBALA R, MANIA R. High temperature CoSb3–Cu junctions., 2011, 51(7): 1198–1202.

[20] GU M, XIA X, LI X,Microstructural evolution of the interfacial layer in the Ti–Al/Yb0.6Co4Sb12thermoelectric joints at high temperature., 2014, 610: 665–670.

[21] TANG Y S, BAI S Q, REN D D,Interface structure and electrical property of Yb0.3Co4Sb12/Mo-Cu element prepared by welding using Ag-Cu-Zn solder., 2015, 30(3): 256–260.

[22] GU M, BAI S, WU J,A high throughput strategy to screen interfacial diffusion barrier materials for thermoelectric modules., 2019, 34(7): 1179–1187.

[23] CHEN L, BAI S, LIU R,Interface stability of skutterudite thermoelectric materials/Ti88Al12., 2018, 33(8): 889–894.

[24] EL-GENK M S, SABER H H, CAILLAT T,Tests results and performance comparisons of coated and un-coated skutterudite based segmented unicouples., 2006, 47(2): 174–200.

[25] HSUEH C H. Thermal stresses in elastic multilayer systems., 2002, 418: 182–188.

[26] HAN M, HUANG J, CHEN S. The influence of interface morphology on the stress distribution in double-ceramic-layer thermal barrier coatings., 2015, 41(3): 4312–4325.

[27] LI Y, YANG X Q, ZHAI P C,Thermal stress simulation and optimum design of CoSb3/Bi2Te3thermoelectric unicouples with graded interlayers., 2008, 973: 297–302.

[28] JIA X, GAO Y. Estimation of thermoelectric and mechanical performances of segmented thermoelectric generators under optimal operating conditions., 2014, 73(1): 335–342.

[29] GU M, XIA X, HUANG X,Study on the interfacial stability of p-type Ti/CeFeCo4–Sb12thermoelectric joints at high temperature., 2016, 671: 238–244.

服役条件下方钴矿基热电元件的界面应力分析

邵笑1,2, 刘睿恒1,3, 王亮1, 初靖1,2, 白光辉4, 柏胜强1,3, 顾明1, 张丽娜4, 马伟4, 陈立东1,3

(1. 中国科学院上海硅酸盐研究所, 高性能陶瓷和超微结构国家重点实验室, 上海 201899; 2. 中国科学院大学, 北京 100049; 3. 中国科学院大学材料科学与光电技术学院, 北京 100049; 4. 空间物理重点实验室, 北京, 100076)

热电器件中, 界面可靠性是影响整体稳定和功率输出的关键因素。对于方钴矿(SKD)器件, 热电臂和电极通过扩散阻挡层(DBL)连接。在高温下, DBL与SKD、电极之间会发生反应并生成复杂的界面结构, 导致界面附近的热、电、力学性能发生变化。本研究根据实际界面结构建立了包含微观结构的有限元模型, 并将其用于分析方钴矿基元件的界面应力状态。采用单层模型对DBL材料参数进行了筛选, 发现热膨胀系数()和弹性模量()对第一主应力有显著影响。采用包含界面微结构的多层模型定量模拟了不同老化温度、时间下元件内部的应力分布, 结果表明在SKD/Zr和SKD/Nb中, CoSb2反应层最为薄弱, 随着老化时间的延长, 反应层的厚度增加, 界面应力变大。同时, 元件的拉伸试验结果与计算结果吻合较好, 验证了模型的准确性与可行性。本研究为提升SKD/DBL元件的结构稳定性提供了指导, 同时也为精确模拟多层结构中的应力状态提供了研究思路。

热电元件; 扩散阻挡层; 有限元模型; 拉伸强度

Supporting information:

Interfacial Stress Analysis on Skutterudite-based Thermoelectric Joints under Service Conditions

SHAO Xiao1,2, LIU Rui-Heng1,3, WANG Liang1, CHU Jing1,2, BAI Guang-Hui4, BAI Sheng-Qiang1,3, GU Ming1, ZHANG Li-Na4, MA Wei4, CHEN Li-Dong1,3

Table A1 Basic properties including molar mass, density, Young’s modulus, Poisson’s ratio, thermal conductivity, thermal expansions and heat capacity for series of materials

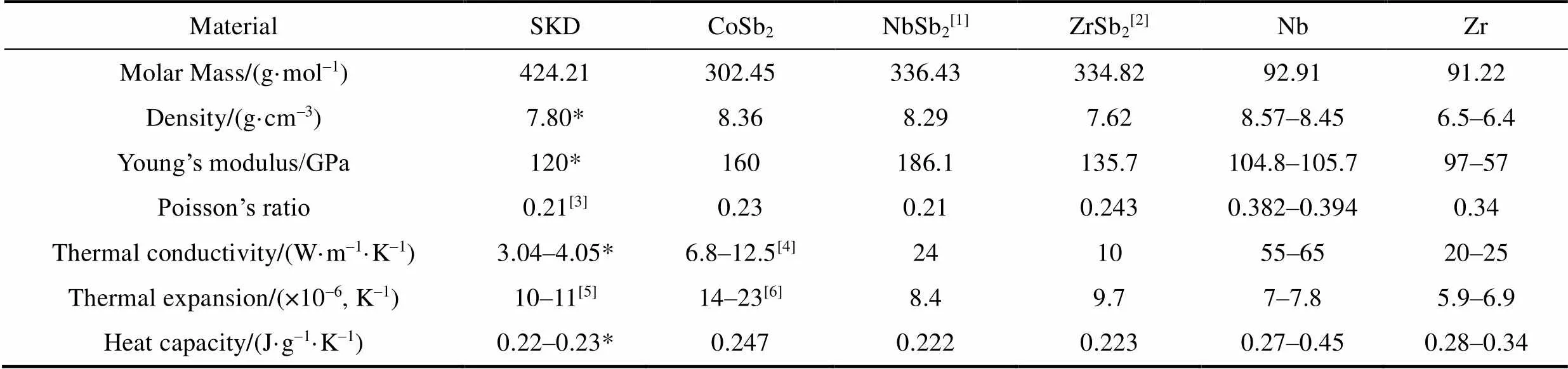
MaterialSKDCoSb2NbSb2[1]ZrSb2[2]NbZr Molar Mass/(g·mol–1)424.21302.45336.43334.8292.9191.22 Density/(g·cm–3)7.80*8.368.297.628.57–8.456.5–6.4 Young’s modulus/GPa120*160186.1135.7104.8–105.797–57 Poisson’s ratio0.21[3]0.230.210.2430.382–0.3940.34 Thermal conductivity/(W·m–1·K–1)3.04–4.05*6.8–12.5[4]241055–6520–25 Thermal expansion/(×10–6, K–1)10–11[5]14–23[6]8.49.77–7.85.9–6.9 Heat capacity/(J·g–1·K–1)0.22–0.23*0.2470.2220.2230.27–0.450.28–0.34

* Properties of Nb and Zr come from COMSOL’ s materials database; Heat capacity of CoSb2and NbSb2are calculated by Dulong-Petit law; Data of SKD are obtained by previous experimental results

Fig. A1 (a) Finite element model of SKD/Nb joint with pores, detailed meshes of (b) NbSb2layer and (c) CoSb2layer

Fig. A2 Interface structures and line scans of joints

(a) As-prepared; (b) Aged at 600 ℃ for 5 d; (c) Aged at 600 ℃ for 10 d; (d) Aged at 650 ℃ for 5 d; (e) Aged at 650 ℃ for 10 d

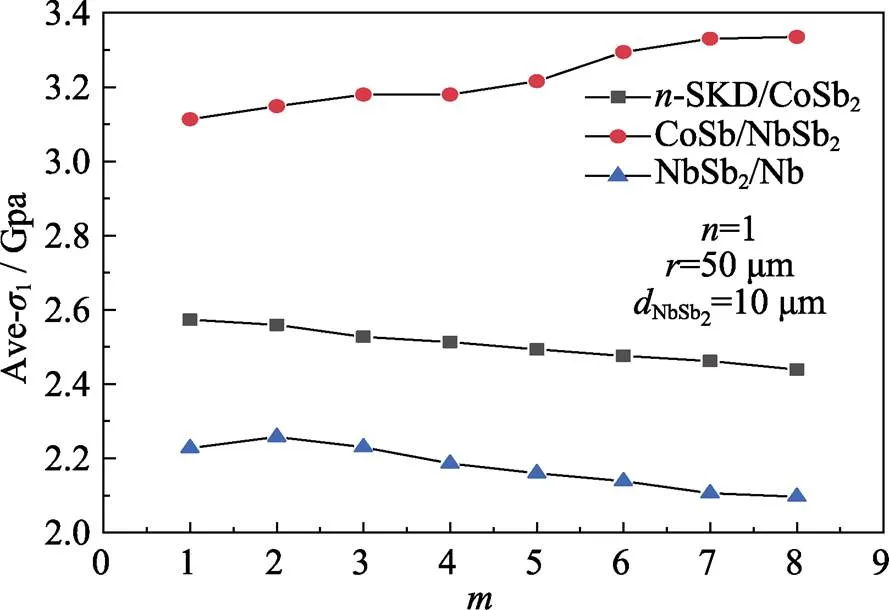
Fig. A3 Relationships between interface stresses and pores major axis ratios

Fig. A4 (a) Calculated stress state of SKD/Zr joint with the Zr layer of 25 μm and the micropores numberof 3; (b) Variation of average1on SKD/CoSb2interface with thickness of ZrSb2and Zr (=3); (c) Variation of average1on CoSb2/ZrSb2interface with thickness of ZrSb2and Zr (=3); (d) Variation of average1on ZrSb2/Zr interface with thickness of ZrSb2and Zr (=3)

[1] FAILAMANI F, BROZ P, MACCIÒ D,Constitution of the systems {V,Nb,Ta}-Sb and physical properties of di-antimonides {V,Nb,Ta}Sb2., 2015, 65: 94–110.

[2] TAVASSOLI A, GRYTSIV A, FAILAMANI F,Constitution of the binary M-Sb systems (M=Ti, Zr, Hf) and physical properties of MSb2., 2018, 94: 119–132.

[3] SALVADOR J R, YANG J, SHI X,Transport and mechanical properties of Yb-filled skutterudites., 2009, 89(19): 1517-1534.

[4] GOTO Y, MIYAO S, KAMIHARA Y,Electrical/thermal transport and electronic structure of the binary cobalt pnictides CoPn2(Pn=As and Sb)., 2015, 5(6): 067147.

[5] ZHAO D, LI X, JIANG W,Fabrication of CoSb3/MoCu thermoelectric joint by one-step SPS and evaluation., 2009, 24(3): 545–548.

[6] BÖRNSTEIN L. CoSb2: Crystal Structure, Physical Properties, in: Madelung U R O, Schulz M (Ed.), Non-tetrahedrally Bonded Binary Compounds ii. Berlin: Springer-Verlag, 2000.

TQ174

1000-324X(2020)02-0224-07

10.15541/jim20190112

2019-03-18;

2019-04-30

National Key Research and Development Program of China (2018YFB0703600); National Natural Science Foundation of China (51572282, 51632010, 11572050); Youth Innovation Promotion Association CAS

SHAO Xiao (1995–), male, Master candidate. E-mail: shaoxiao@student.sic.ac.cn

邵笑(1995–), 男, 硕士研究生. E-mail: shaoxiao@student.sic.ac.cn

Corresponding author:LIU Rui-Heng, associate professor. E-mail: liurh@mail.sic.ac.cn

刘睿恒, 副研究员, E-mail: liurh@mail.sic.ac.cn