应力波在落叶松活立木中传播影响因素数值模拟

刘丰禄 张厚江 王喜平 姜 芳 管 成

(1.北京林业大学工学院， 北京 100083； 2.北京林业大学木材无损检测国际联合研究所, 北京 100083;3.美国农业部林务局林产品实验室, 麦迪逊 WI 53726)

0 引言

应力波无损检测技术已在木材工业领域得到了广泛应用[1-8]，但木材性质的高度各向异性和非均匀性使应力波在木材中传播机理的复杂性不同于一般的材料，因此导致以往大部分的研究工作还集中在对波速的直接测量，并以此参数作为木材质量评估与材性预测的基础[6-8]，而涉及应力波在木材中传播机理的研究却不多[9-10]。

随着林业工作者和科研人员对应力波在木材中的传播机理越来越关注，国内外逐渐报道了一些研究成果[11-19]。关于应力波在木材中传播机理的大部分研究主要集中在采用理论建模或试验研究探索应力波在原木或活立木中的传播规律，通过数值模拟的方式对应力波在木材(特别是活立木)中传播的研究很少[20]，而应力波在活立木中传播的影响因素研究更是鲜有报道。目前，大部分研究主要分析活立木胸径对波速的影响。有研究表明，活立木胸径与波速之间不存在显著的相关关系，即活立木胸径对波速几乎没有影响[21-23]；但另有研究则表明，活立木胸径不仅会影响应力波的传播形式，而且对波速也会产生影响[7,9,24]。因此，波速与胸径之间的关系并没有一致的结论，有必要通过数值模拟的方法研究胸径对应力波传播的影响，尤其是对波速的影响。另外，敲击载荷脉冲频率以及活立木心材比等因素对应力波传播的影响，目前尚未见相关研究报道。

本文在上述研究的基础上，通过数值模拟手段对应力波在活立木中传播的影响因素(敲击载荷脉冲频率、活立木胸径和心材比)进行研究，分析这3个因素对应力波传播形式、传播规律以及波速的影响，以期为研究应力波在人工林活立木中的传播机理奠定基础。

1 建模与求解

1.1 活立木几何模型

通常情况下，活立木是由髓心、心材、边材和树皮组成。同时，鉴于活立木是高度各向异性材料，其力学性能从髓心、心材到边材会发生明显的变化。因此，为了便于研究活立木胸径、心材比以及敲击载荷频率对应力波传播的影响，需要对活立木作一些几何模型的简化：将活立木看作正交各向异性材料；将活立木看作两层结构材料即只由心材层和边材层组成，且心材层和边材层均为正交各向异性。

考虑到常见的林分年龄为40 a的华北落叶松人工林，其活立木平均胸径为15～40 cm之间，立木平均尖削度为1～3 cm/m，心材含量与边材含量的比例为6∶4～8∶2[25]。因此，为了使数值模拟的几何模型尽可能接近实际的活立木，同时考虑到活立木的直径沿着树高方向的变异性以及数值模拟的计算量和效率等问题，将活立木几何模型设定为具有一定尖削度的圆柱体模型。构建出两套不同的活立木几何模型用于分别研究活立木的胸径、心材比以及敲击载荷频率对应力波传播的影响。用于研究活立木胸径对应力波传播影响的第1套活立木几何模型，其模型长度L为200 cm，尖削度为2.5 cm/m，心材比为70%，胸径取10、30、50、70、90 cm，第1套活立木几何模型的具体参数如表1(表中D表示活立木模型的大端直径，d表示活立木模型的小端直径，Dh表示心材层的大端直径，dh表示心材层的小端直径，Rh表示活立木模型心材所占百分比(简称心材比))所示，这5个不同胸径活立木模型的大端面示意图如图1所示。

表1 第1套活立木几何模型的尺寸

图1 不同胸径活立木模型的大端面示意图

图1从左到右分别对应表1中的模型1、2、3、4、5，图1中的灰色圆形区域为活立木模型的心材层，白色环带区域则为边材层。以模型3为例，通过软件构造的活立木三维几何模型如图2所示，其中，层1为心材层，层2为边材层，图2中各坐标轴的单位均为cm。

图2 第1套活立木三维几何模型(模型3)

用于研究活立木心材比对应力波传播影响的第2套活立木几何模型，其活立木模型的长度L为200 cm，尖削度为2.5 cm/m，大端直径D为35 cm，小端直径d为30 cm，考虑到不同林分年龄以及生长环境的不同，华北落叶松的心材比也会有所变化，同时为了研究心材比的变化对应力波在活立木中传播的影响，将华北落叶松的心材比范围做了适当的扩大，心材比Rh取50%、60%、70%、80%和90%，第2套活立木几何模型的具体参数如表2所示，这5个不同心材比的活立木模型的大端面示意图如图3所示。

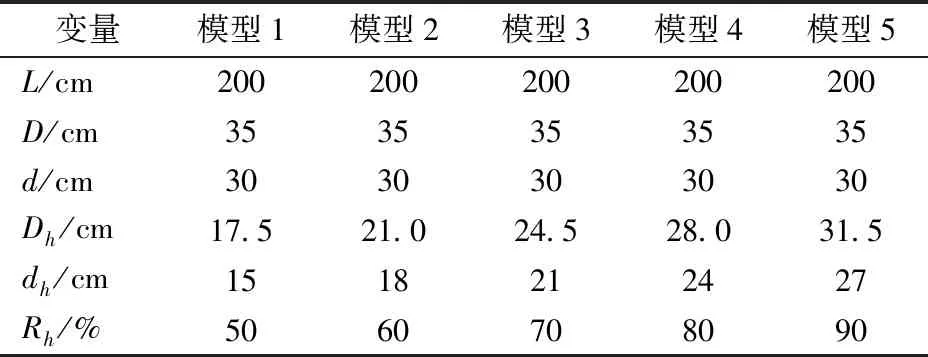
表2 第2套活立木几何模型的尺寸

图3 不同心材比的活立木模型的大端面示意图

图3从左到右分别对应表2中的模型1、2、3、4、5。将表2中模型3的尺寸作为研究敲击载荷频率对应力波传播影响的活立木模型的尺寸，即，用于研究敲击载荷频率对应力波传播影响活立木几何模型的长度L为200 cm，尖削度为2.5 cm/m，大端直径D为35 cm，小端直径d为30 cm，心材层的大端直径Dh为24.5 cm，心材层的小端直径dh为21 cm，心材比Rh取70%。

1.2 材料属性

一般来说，在木材的任何一点，都能识别出3个相互正交的方向，即顺纹纵向L、径向R和弦向T，如图4所示。这些方向可以给出在该点的3个对称面，即正交各向异性模型，所以在许多的研究中也都将木材看作正交各向异性材料[17-18,26-27]。因此，本文将柱状的正交各向异性体选为活立木树干的物理模型，并将活立木树干的3个主轴方向设定为径向R、弦向T、纵向L(分别对应笛卡尔坐标系中的x、y、z)。

图4 木材正交各向异性示意图

活立木心材层和边材层的材料参数取自前期试验通过电测法和三点弯曲法[28]测定的落叶松生材4个不同取样位置的全部12个弹性常数，试验试样取自河北省承德市隆化县茅荆坝林场的人工林落叶松，树龄为40 a，活立木的含水率约为95%，具体参数如表3、4所示。

1.3 载荷设定

根据野外应力波试验方法[29]，如图5所示，在活立木树木内部传播的应力波是通过小锤瞬态敲击输入极产生的，对于这种短历时作用力可采用脉冲函数来描述，故数值模拟计算时采用半正弦脉冲函数来定义导入的应力波，其表达式为

(1)

表4 边材层的弹性常数及密度

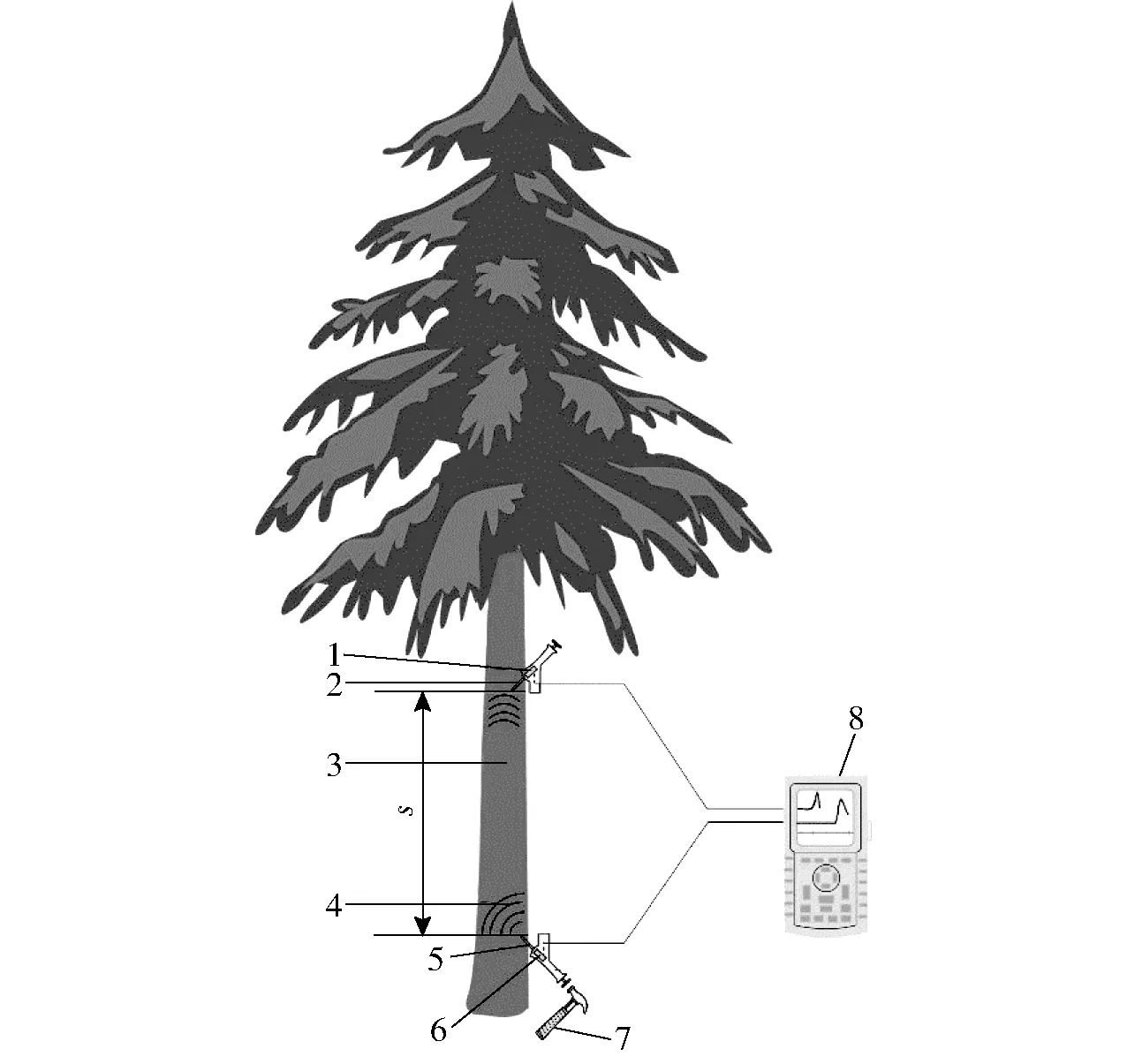
图5 野外应力波测量方法示意图

式中A——脉冲幅值

f——脉冲载荷频率t——时间

根据实测的小锤敲击脉冲力信号(图6)可知，其幅值约为200 N，脉冲频率约为2.5 kHz。

图6 实测的脉冲力信号

从野外应力波测量试验可知，由于导入极与活立木轴线方向呈45°，即脉冲力沿与活立木轴线呈45°方向进入树干，所以根据矢量分解原则，将力F(t)分解为两个分量：Fy(t)和Fz(t)，每个分力幅值为141.4 N。因此，对于活立木模型，可在数值模拟中设定脉冲分力幅值A=141.4 N，脉冲频率f=2.5 kHz。此外，为了研究敲击载荷的频率(也就是脉冲频率f)对应力波传播的影响，在2.5 kHz的脉冲频率的基础上，加入了5、10、15、20、25、30 kHz系列的脉冲频率。

1.4 初始条件和边界条件

(1)初始条件

表示某过程初始时刻状态的条件称作初始条件，包括初位移和初速度。由于活立木模型在受到载荷作用之前一直处于静止的状态，即模型中的各个质点均没有初位移和初速度，因此设介质内各质点的初位移和初速度均为零。

(2)边界条件

表示某过程物理量在系统的边界上所满足的物理条件称为边界条件，通常情况下边界条件可以分为3类：①第1类边界条件：直接给出物理量在边界上的数值。②第2类边界条件：给定未知量在边界上的法向导数值。③第3类边界条件：给出边界上未知函数及其法向导数间的线性关系。本文采用两类边界条件：自由边界条件(即第2类边界条件)和低反射边界条件(即第3类边界条件)。所谓自由边界条件是指当应力波传到模型边界上时，透射波和反射波同时存在，并伴随波的衰减，而低反射边界条件是指当应力波传到模型远端面边界处时，只有透射波而没有反射波存在或者有极少量的反射波。这两种边界条件的数学表达式为：

自由边界条件

(2)

式中u——质点位移

l——边界的单位法向量

r——模型半径

低反射边界条件

(3)

式中σ——质点所受的应力

n——边界的单位法向量

m——边界的单位切向量

Cp——纵波波速Cs——剪切波波速

ρ——介质密度

考虑到活立木的实际边界条件，在数值模拟时将活立木模型的侧面设置为自由边界条件，模型的端面则为低反射边界条件，从而使数值模拟与实际情况相一致。

1.5 网格划分和求解设定

采用扫掠的方法对活立木三维模型进行网格划分，以第2套活立木模型的模型1为例，先对活立木三维模型的大端端面采用自由剖分的三角形网格来进行网格划分，对于心材层，其最大单元尺寸为2 cm，最小单元尺寸为0.004 cm，对于边材层，其最大单元尺寸为1.4 cm，最小单元尺寸为0.004 cm，完成大端端面处的网格划分后，采用扫掠的方式将网格扫掠至模型的小端面，从而拓展到整个三维几何模型，扫掠法采用的分布单元数为40，整个三维模型网格划分后的总单元个数为35 040。图7为第2套活立木模型的模型1划分后的网格情况。数值模拟的求解步长设定如下：瞬态求解器采用的时间步长为广义α算法的自由方式，初始步长为1×10-9s，最大步长设为1×10-4s；计算时间步长为1×10-6s，输出求解结果的步长为1×10-6s。

图7 活立木模型三维网格划分示意图(模型1)

2 数值模拟

2.1 敲击载荷频率对应力波传播的影响

2.1.1三维应力波传播波阵面

为了能直观形象地显示应力波波阵面在活立木模型中的传播形式，通过提取数值模拟获得的多个时间节点(100、150、200、250、300、350、400、450 μs)的三维位移等值面图最前端的等值面，得到应力波在不同敲击载荷频率的活立木模型中的三维传播波阵面图，如图8所示，图中各个活立木模型右下角的圆点为应力波的导入点，黑色箭头表示应力波的导入方向不同。从图8可以看出，在不同脉冲频率的活立木模型中，应力波的三维传播波阵面的形状以及传播形式基本相同，均是在开始阶段以弯向应力波导入点的倾斜曲面形式传播，之后，随着传播距离的增大，波阵面的倾斜程度逐渐减小，波阵面逐渐趋向垂直于活立木模型的长度方向。也就是说，敲击载荷的频率对应力波在活立木模型中的传播形式以及波阵面的形状没有影响。从图8中还可以发现，应力波的波阵面在活立木模型中的传播距离随着载荷脉冲频率的增大逐渐减小。对于同一数值模拟时间节点450 μs，应力波在脉冲频率为2.5 kHz的活立木模型中传播距离最远，而在脉冲频率为30 kHz的活立木模型中传播距离最近。对于其他的数值模拟时间节点，同样可以发现传播距离随载荷脉冲频率的增大而减小。因此，对于活立木模型，敲击载荷频率对应力波的传播形式以及波阵面形状没有影响，但对应力波的传播距离有影响。

图8 不同脉冲频率下的三维应力波传播波阵面图

2.1.2敲击载荷频率对应力波波速的影响

根据不同脉冲频率活立木模型的应力波数值模拟结果(图8)可知，对于活立木模型，敲击载荷频率对应力波的传播形式以及波阵面形状没有影响，但对应力波的传播距离有影响。在相同传播时间内，应力波传播距离的差异实质上是传播速度的差异，即敲击载荷频率对应力波的传播速度有影响。为了进一步研究敲击载荷频率与波速之间的关系，根据数值模拟结果计算了应力波在不同脉冲载荷频率活立木模型中的传播速度，并得到了应力波波速与载荷脉冲频率的关系，如图9所示。

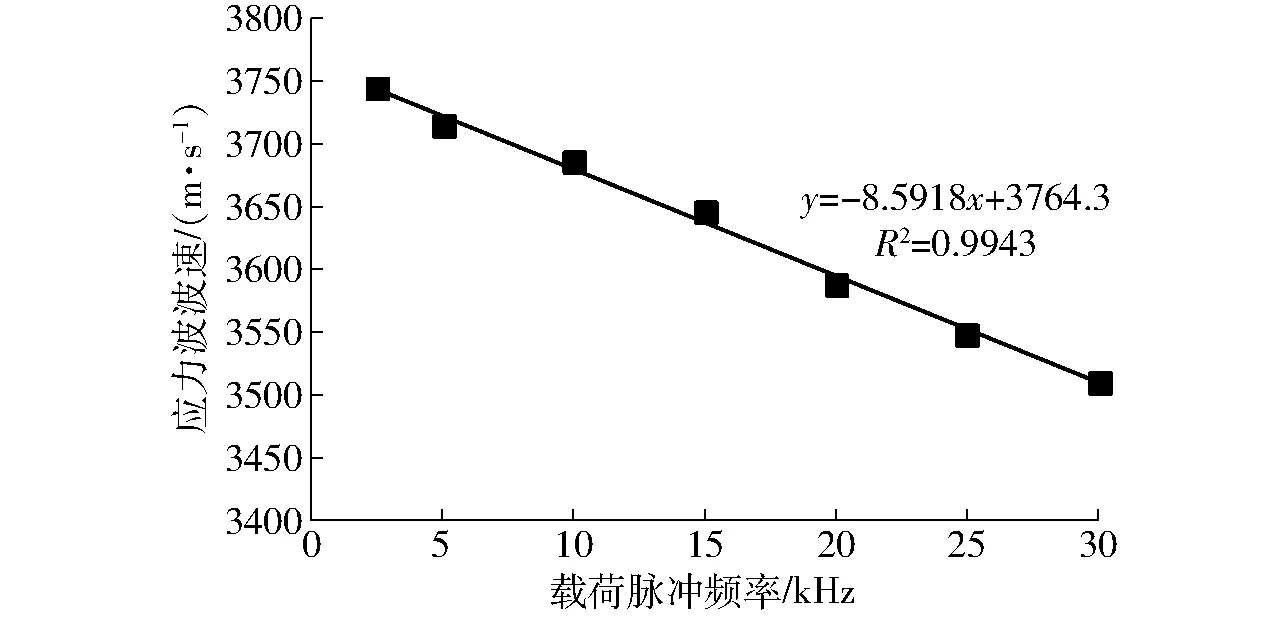
图9 应力波波速与载荷脉冲频率的关系

从图9可知，对于不同载荷脉冲频率的活立木模型，应力波在其中的传播速度是不同的，应力波波速随着载荷脉冲频率的增大而减小，这与在应力波三维传播波阵面中发现的结论一致，造成这一现象的原因可能是载荷脉冲信号的衰减随着脉冲信号频率的增大而增加，即更高的脉冲频率会造成更大的脉冲信号衰减率，导致应力波的传播速度变慢[30-31]。综上所述，数值模拟结果表明敲击载荷的频率虽然不会影响应力波在活立木中的传播形式以及波阵面形状，但会影响应力波的传播速度，因此需要选择最佳的频率使得数值模拟结果更加符合实际情况。考虑到实测的敲击信号频率约为2.5 kHz，且在这个频率时数值模拟得到的活立木波速与实测的波速(3 775 m/s)更加接近，因此数值模拟最佳的敲击载荷频率为2.5 kHz，下文中所有数值模拟采用的敲击载荷频率均为2.5 kHz。

2.2 胸径对应力波传播的影响

2.2.1三维应力波传播波阵面

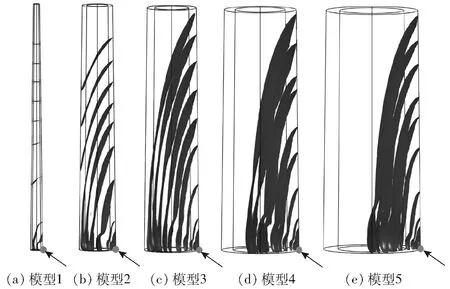
图10 应力波在第1套活立木模型中的三维传播波阵面

为了研究活立木胸径对应力波传播波阵面的影响，提取传播时间节点100、150、200、250、300、350、400、450、500 μs的三维位移等值面图最前端的等值面，形成三维应力波传播波阵面图。图10为应力波在5个不同胸径的活立木模型中传播的三维波阵面传播图。由图10可知，应力波在5个不同胸径活立木模型中的传播形式以及波阵面的形状不相同，存在一定的差异。对于胸径最小的活立木模型1(大端直径D=10 cm)，当传播时间t达300 μs时，应力波的波阵面已经从三维膨胀波转换为一维平面波。然而，对于活立木模型2(D=30 cm)，当传播时间为500 μs时，应力波的波阵面仍然处于三维膨胀波的状态，但波阵面的倾斜度已明显减小，这可能说明波阵面正在向一维平面波的形式转换。对于胸径更大的活立木模型3(D=50 cm)、4(D=70 cm)和5(D=90 cm)，同样在传播时间为500 μs时，应力波的波阵面不仅处于三维膨胀波的状态，而且波阵面的倾斜度仍然很大，还存在拉长的现象，应力波在这3个活立木模型中的传播波阵面可能需要更长的时间和传播距离才能从三维膨胀波转换为一维平面波。此外，从图10还可以看出，活立木胸径似乎也对应力波的传播速度有影响。当传播时间为500 μs时，应力波波阵面在活立木模型2中的传播距离略大于活立木模型1中的传播距离。然而，在相同的传播时间下，波阵面在活立木模型3中的传播距离明显大于在活立木模型2中的传播距离。不过，应力波在活立木模型4、5中的传播距离与在活立木模型3中的传播距离相比，发现三者的传播距离几乎相同，没有明显的差异。因此，应力波在活立木模型中的传播速度可能受活立木胸径的影响。

在关于应力波在活立木中传播的研究中，Fakopp(应力波微秒计)常被用于测量应力波在活立木中的传播时间。通常情况下，Fakopp的发射端放置在离地面50～60 cm处，接收端放置在距发射端1.2 m的位置，这意味着使用Fakopp测量应力波活立木中的传播时间实际上等于测量从发射端到接收端1.2 m距离内应力波的传播过程。另外，考虑到不同树龄和树种间的胸径存在显著差异，因此以华北落叶松为例，对于树龄为40 a的华北落叶松，其胸径一般在30～50 cm之间。从图10可以发现，对于胸径为30 cm和50 cm的活立木模型(即活立木模型2、3)，当应力波的传播距离达到1.2 m时，应力波的波阵面仍然是三维膨胀波的波阵面，这意味着应力波在活立木模型0～1.2 m的传播距离范围内是以三维膨胀波的形式传播。因此，对于胸径大于30 cm的活立木而言，在1.2 m的测量距离范围内，用Fakopp获得的活立木应力波波速可能是三维膨胀波的传播速度而不是一维平面波的传播速度。此外，文献[7]研究发现辐射松活立木波速与原木波速的比值随着胸径的增加而增加，当胸径变小时，活立木波速与原木波速的比值减小，测得的活立木波速更接近原木波速。随着胸径逐渐增加，该比值增加，导致活立木波速大于原木波速。从图10可以看出，对于胸径为10 cm的活立木模型(即模型1)，当传播距离达到1.2 m时，应力波波阵面已经转化为一维平面波，即，对于胸径较小的活立木，用Fakopp测量得到的波速可能是一维平面波的传播速度，而在许多研究中都假设在原木中测得的应力波波速是一维平面波波速，因此，活立木波速与原木波速较为接近，这与文献[7]的结果一致。而当活立木模型的胸径达到30 cm或更大时，应力波在0～1.2 m的传播距离内是以三维膨胀波的形式传播，即，此时应力波在活立木模型中的传播速度可能是膨胀波波速而不是一维平面波波速。这可以用来解释文献[7]发现当活立木胸径增大时，活立木波速与原木波速的比值增加，导致活立木波速高于原木波速。

2.2.2胸径对应力波波速的影响

由前文可知，胸径对应力波在活立木中的传播形式以及波阵面形状有影响，同时还发现胸径可能会对应力波的传播距离以及传播速度产生影响。为了进一步分析胸径与波速之间的关系，计算出了应力波在5个不同胸径的活立木模型中传播速度(在传播距离为1.2 m处)，并给出了活立木胸径、立木长径比(L/D)与应力波波速之间的关系，如图11所示。从图11可以看出，当胸径小于10 cm时，波速较小且基本没有发生变化，当胸径从10 cm变化到40 cm时，应力波波速随着胸径的增加而增加，当活立木胸径超过40 cm后，波速略微增加后保持相对稳定。另外，计算结果表明应力波在胸径为5 cm和10 cm的活立木模型中传播速度分别为3 345 m/s和3 347 m/s，这两个数值略大于由所测得华北落叶松弹性常数平均值和密度计算出来的一维平面波的理论波速(3 335 m/s)。而应力波在胸径为90 cm的活立木模型中传播速度为3 918 m/s，略小于理论三维膨胀波波速(3 935 m/s)。可以预测，当活立木模型的胸径小于10 cm后，数值模拟得到的波速将会逐渐变为一维平面波的理论波速，而当活立木模型的胸径大于90 cm后，数值模拟得到的应力波波速也会变为三维膨胀波理论波速。因此，当胸径小于10 cm时，在野外活立木应力波传播试验常用的测量距离范围内(通常为1.2 m)，应力波可能是以一维平面波的形式在活立木中传播，而当胸径超过40 cm后，应力波将可能以三维膨胀波的形式在活立木中传播。对于树龄为40 a的华北落叶松，胸径达到10 cm和40 cm似乎是应力波波速变化的拐点，一维平面波的波速转换点为10 cm，三维膨胀波的波速转换点为40 cm。这个拐点值可能会随树种和林龄的变化而发生改变。

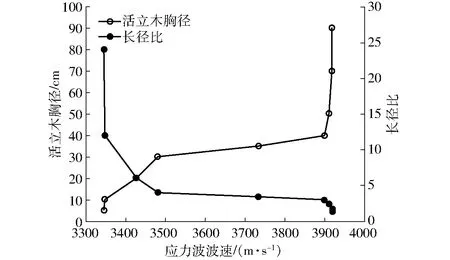
图11 应力波波速与活立木胸径关系

活立木胸径与波速之间的关系没有一致的发现和结论。文献[1]对不同林分的树林研究发现应力波传播速度与活立木胸径之间几乎没有相关性，这与文献[32-34]在活立木上发现的结果相类似。然而，文献[22,35-36]却发现对于幼林树，由Fakopp测得的活立木波速与胸径之间存在负相关关系。此外，文献[7]发现活立木胸径与波速之间存在正相关关系，并提出了一种基于以活立木胸径为自变量的简单非线性模型波速修正方法。从数值模拟结果(图11)可知，活立木胸径对应力波传播速度有影响。当胸径大于10 cm而小于40 cm时，波速随着胸径的增大而增大，这与文献[7]的结果基本一致。

2.3 心材比对应力波传播的影响

2.3.1三维应力波传播波阵面

为了进一步研究活立木的心材比对应力波传播波阵面的影响，提取传播时间节点100、150、200、250、300、350、400、450、500 μs的三维位移等值面图最前端的等值面，形成三维应力波传播波阵面图，得到应力波在5个不同心材比的活立木模型中传播的三维波阵面传播图，如图12所示。

图12 应力波在第2套活立木模型中的三维传播波阵面

从图12可以看出，应力波在5种不同心材比的活立木模型中的传播形式及规律具有相似性和差异性。相似之处在于，应力波在这5种不同心材比活立木模型中具有相同的传播规律：应力波的波阵面在开始阶段是以一个弯向脉冲输入点的不规则倾斜曲面向前传播，之后随着传播时间的增加，波阵面逐渐转变为规则的倾斜曲面，且波阵面的曲率逐渐减小，最后，波阵面逐渐向垂直于活立木模型主轴的方向变化。不同之处在于，应力波在这5种不同心材比的活立木模型中传播距离不同。从图12中可以看到，在相同的传播时间(以500 μs为例)内，与其他活立木模型相比，应力波在心材比为50%的活立木模型中传播距离最远。随着心材比的增加，应力波在活立木模型中传播的距离逐渐减小。因此，根据相同传播时间内，应力波传播距离与活立木心材比呈负相关关系，可以进一步得出应力波波速与活立木心材比也可能具有负相关性，这表明应力波传播速度与活立木的心材比有关，应力波波速可能会随着活立木心材比的增加而减小。从上述这些数值结果可以得出，活立木心材比对应力波的传播形式及波阵面形状没有影响，但对应力波在活立木中的传播距离有影响。

2.3.2心材比对应力波波速的影响

从应力波三维传播波阵面图(图12)中已经可以看出，活立木的心材比对应力波的传播速度有影响，活立木心材比与波速之间存在相关性。为了进一步分析活立木模型的心材比与应力波传播速度之间的关系，通过数值模拟计算了应力波在不同心材比活立木模型中的传播速度(在传播距离为1.2 m处)，并得到了活立木心材比与应力波波速之间的关系，如图13所示。从图13可以看出，活立木的心材比对应力波的传播速度有影响，应力波在活立木模型中的传播速度随着心材比的增加而减小。这可能是因为心材的纵向弹性模量(Modulus of elasticity，MOE)远低于边材的纵向弹性模量，随着活立木模型中心材比的增加，边材的纵向弹性模量对应力波传播的影响越来越小，心材的纵向弹性模量将主导应力波的传播，而应力波的纵向传播速度是最快的，从而导致应力波的传播速度减小。

图13 应力波波速与活立木心材比关系

目前，在有关应力波传播的研究中已经发现，在活立木上测得的波速比在原木上测得的波速高7%～36%。文献[22,32-34]认为导致活立木波速大于原木波速的原因是在活立木上测应力波传播时间所采用的飞行时间法(Time-of-flight)测得的只是应力波在边材中的传播速度，而不是在整个活立木中的传播速度。然而，从活立木的心材比与应力波波速之间的关系图(图13)可以看出，活立木心材比对波速有影响，波速随着心材比的增大而减小。根据文献[34]提出的假设，如果在活立木中测得的应力波波速是边材的波速，则当活立木的心材比变化时，应力波的波速应该不会受到影响。根据数值模拟得到的结果可以发现，当活立木模型的心材比从40%增加到90%时，相对应的应力波波速从大约4 000 m/s减小到3 400 m/s，波速降低约15%，这说明波速反映的是应力波在整个活立木模型中的传播速度，而不是在边材中的传播速度，应力波在活立木中的传播可能同时受到心材和边材的影响，即应力波在活立木中的传播速度同时受到心材和边材的影响。因此，使用飞行时间法测得的是应力波在边材中的传播速度来解释在活立木中测得波速高于在原木中测得波速的原因可能是不合理的。对于这个问题更为合理的解释可能是应力波在活立木和原木中的传播机理不同，应力波在活立木中可能是以三维膨胀波的形式传播，而在原木中则可能是以一维平面波的形式传播。由前文数值模拟得到的应力波在不同胸径活立木模型中的三维传播波阵面(图10)可知，对于胸径在30～90 cm的活立木模型，应力波在传播至1.2 m处之后并没有转化为一维平面波形式，仍然是三维膨胀波的形式，而应力波在原木中往往被看作是以一维平面波形式的传播，从而导致活立木波速要大于原木波速，这与文献[7]观点相符。

3 结论

(1)敲击载荷频率对应力波在活立木中的传播形式、规律以及波阵面形状没有影响，但会影响应力波在其中的传播速度，应力波的波速随着载荷脉冲频率的增大而减小，数值模拟最佳的敲击载荷频率为2.5 kHz。

(2)活立木胸径对应力波的传播形式以及波阵面形状有影响，对于胸径为10 cm的活立木模型，当传播距离达到1.2 m时，应力波波阵面已经转换为一维平面波，而对于胸径超过30 cm的活立木模型，应力波在0～1.2 m传播距离内是以三维膨胀波的形式传播；活立木胸径对应力波的传播速度有影响，当活立木胸径小于10 cm时，波速较小且基本没有发生变化，当活立木胸径从10 cm增加到40 cm时，应力波的波速随着活立木胸径的增加而增加，而活立木胸径超过40 cm时，波速略微增加后保持相对稳定。

(3)心材比对应力波在活立木中的传播形式、规律以及波阵面形状没有影响，但会影响应力波的传播速度，应力波在活立木中的波速随着心材比的增大而减小；应力波在活立木中的传播速度不只取决于边材的力学性能，而是受到心材和边材的共同影响。