串并联系统可靠度置信下限计算方法
2020-03-08傅惠民文歆磊杨海峰
傅惠民, 文歆磊, 杨海峰
(北京航空航天大学 小样本技术研究中心, 北京 100191)
0 引言
众所周知, 由相互独立的子系统组成的串联系统可靠度等于各子系统可靠度的乘积,但是,串联系统可靠度单侧置信下限是否也等于各子系统可靠度单侧置信下限的乘积?同样,并联系统不可靠度等于各子系统不可靠度的乘积, 而并联系统不可靠度单侧置信上限是否也等于各子系统不可靠度单侧置信上限的乘积? 这一问题长期以来没有得到严格证明, 因此工程上一般不敢将子系统的置信限简单相乘。 文献[1]还通过实例计算说明置信限不能相乘,而文献[2]则指出文献[1]的实例计算有误,但也承认这一问题还没有得到严格证明。 串联和并联是工程上主要的系统连接形式, 其可靠度置信下限计算极其重要。 因此,人们先后提出了计算串联系统可靠度置信下限的LM 法、MML 法、SR 法等[3]和计算并联系统可靠度置信下限的LR 法、AWI 法、ML 法、AO 法等[4],然而这些方法都无法考虑无失效数据子系统的失效可能性, 导致整个系统可靠度置信下限误差较大,且偏于危险。
本文对此进行了深入系统的研究, 首先建立了串并联系统各子系统置信限相乘的置信度干涉模型计算方法, 严格证明了串联系统可靠度单侧置信下限等于各子系统可靠度单侧置信下限的乘积, 并联系统不可靠度单侧置信上限等于各子系统不可靠度单侧置信上限的乘积,成功解决了这一难题。
1 串联系统可靠度置信下限
设系统由m 个相互独立的子系统(或部件、单元等)串联构成,Ri为第i 个子系统的可靠度,则串联系统可靠度R 等于各子系统可靠度Ri的乘积

定理1 设串联系统的各子系统相互独立, RL,i为第i个子系统可靠度Ri的置信水平为γ(γ≥50%)的单侧置信下限

则该串联系统可靠度R 的置信水平为γ 的单侧置信下限RL由下式给出

即串联系统可靠度单侧置信下限RL等于各子系统可靠度单侧置信下限RL,i的乘积。
下面分两种情况对定理1 进行证明。 对于各子系统完全相同且相互独立的情况,由于

所以

由此可知定理1 成立,证毕!
对于各子系统不完全相同且相互独立的情况, 首先证明下面的引理。
引理设串联系统由两个相互独立的子系统构成,RL,i为第i 个子系统可靠度Ri的置信度为γi的单侧置信下限

令该串联系统可靠度R 的单侧置信下限RL=RL,1RL,2,则其置信度由下式计算

式中,X1=R1/RL,1,X2=RL,2/R2。
根据引理可知, 由两个相互独立的子系统构成的串联系统可靠度R 的单侧置信下限为RL=RL,1RL,2,其置信度可以通过随机变量X1=R1/RL,1和X2=RL,2/R2的干涉模型计算。 当γ1=γ2=γ(γ≥50%)时,有

因此

随机变量X1和X2的干涉模型如图1 所示, 将X1和X2的概率密度函数绘制于同一坐标系下, 直线x=1 将X1的概率密度曲线下方的区域分割为区域A1和A2,将X2的概率密度曲线下方的区域分割为区域A3和A4。其中,区域A1和A3的面积均为γ,区域A2和A4的面积均为1-γ。
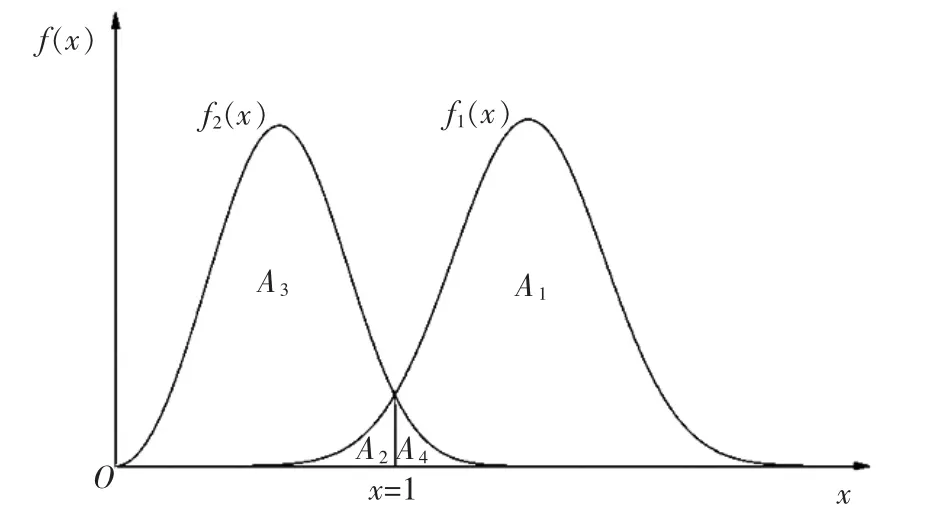
图1 X1 和X2 的干涉模型
(1)X1在区域A1取值的概率为γ、X2在区域A3取值的概率也为γ,此时事件X1≥X2发生的概率为γ2,即

(2)X1在区域A2取值的概率为1-γ、X2在区域A4取值的概率也为1-γ,此时事件X1≤X2发生的概率为(1-γ)2,即

(3)X1在区域A1取值的概率为γ、X2在区域A4取值的概率为1-γ; 或X1在区域A2取值的概率为1-γ、X2在区域A3取值的概率为γ,显然,此时事件X1≥X2发生的概率要大于事件X1≤X2发生的概率[5]。 因此,有

综合上述X1和X2取值的三种情况可知,有

将X1=R1/RL,1,X2=RL,2/R2代入得

当γ(γ≥50%)为置信水平时,即

式(20)也同样成立。 因此,对于两个相互独立的子系统构成的串联系统,定理1 成立。若串联系统包含m 个相互独立的子系统, 可以先将前两个子系统可靠度的单侧置信下限相乘,再将这两个串联子系统看作一个新的子系统,与第3 个子系统可靠度的单侧置信下限相乘,以此类推,即可证明当系统由m 个相互独立的子系统串联构成时,定理1 也成立。 证毕!
2 并联系统可靠度置信下限
设系统由m 个相互独立的子系统(或部件、单元等)并联构成,Ri为第i 个子系统的可靠度,则并联系统可靠度R 为

定理2 设并联系统的各子系统相互独立,RL,i为第i 个子系统可靠度Ri的置信水平为γ(γ≥50%)的单侧置信下限
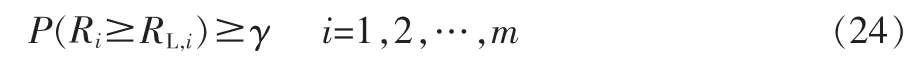
则该并联系统可靠度R 的置信水平为γ 的单侧置信下限RL由下式给出

即并联系统不可靠度1-R 的单侧置信上限1-RL等于各子系统不可靠度1-Ri的单侧置信上限1-RL,i的乘积。
同样,下面分两种情况对定理2 进行证明。 对于各子系统完全相同且相互独立的情况,即式(5)和式(6)成立。此时有

即定理2 成立,证毕!
对于各子系统不完全相同且相互独立的情况, 令F=1-R,FU=1-RL,Fi=1-Ri,FU,i=1-RL,i。当系统仅由两个相互独立的子系统并联构成时, 其可靠度R=1-F1F2的单侧置信下限RL=1-FU,1FU,2的置信度由下式计算
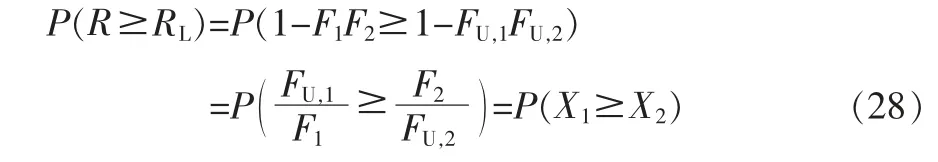
式中,X1=FU,1/F1,X2=F2/FU,2。
若

则

由式(14)、式(15)和式(19)可知,有

将X1=FU,1/F1,X2=F2/FU,2代入上式,得

同理可证, 对于m 个相互独立的子系统构成的并联系统,定理2 也成立。 证毕!
3 传统方法及其存在的问题
3.1 成败型串联系统可靠度置信下限计算方法
成败型串联系统在工程中较为常见,应用十分广泛。 当前, 常用的成败型串联系统可靠性评估方法包括LM 法,MML法和SR 法等,下面简单讨论这些方法及其存在的问题。
3.1.1 LM法
Linstrom 和Madden 建立了成败型串联系统可靠度的近似限。 设第i 个子系统在ni次试验中成功si次,i=1,2,…,m。 令

即可得到系统的等效试验数n 和成功数s,进而根据二项分布可靠性置信下限分析方法求得给定置信度γ 下的系统可靠度单侧置信下限RL。
从式(35)和式(36)可以看出,LM 方法不能很好地处理无失效试验数据,下面进行详细讨论。
(1)当所有子系统的试验结果均为无失效数据时,易得s=n=min{n1,n2,…,nm},这导致系统的可靠度置信下限仅等于试验次数最少的子系统可靠度置信下限,而没有考虑其他子系统失效的可能性,因此可靠性评估结果偏于危险。
(2)当部分子系统的试验结果为无失效数据,且试验次数最少的子系统有失效数据时,由式(35)和式(36)可知, 这导致所有无失效数据的子系统试验结果均对系统可靠度置信下限没有贡献, 即也没有考虑串联系统中无失效数据子系统的失效可能性,因此结果偏于危险。
(3)当部分子系统的试验结果为无失效数据,且试验次数最少的子系统没有失效数据时,由式(35)和式(36)可知,这导致仅有该子系统的试验次数参与了系统可靠度置信下限的计算,其余无失效数据的子系统试验结果同样也都对系统可靠度置信下限没有贡献,因此结果偏于危险。
3.1.2 MML法
修正极大似然估计法(MML 法)由Easterlin 提出。 对于m 个相互独立子系统构成的成败型串联系统, 其等效试验次数n、成功次数s 分别由下面两式求得,在此基础上进一步得到系统可靠度单侧置信下限RL。


从式(37)和式(38)不难发现,当子系统的试验结果为无失效数据时, 相应的ni和si对n 和s 的计算没有任何贡献,即MML 方法也不能考虑无失效数据子系统失效的可能性, 从而使系统可靠性评估结果偏于危险。 特别地,当所有子系统的试验结果均为无失效数据时,式(37)出现0/0 的情况,已无意义。
3.1.3 SR法
为克服MML 法的局限性,Preston 进一步提出了序贯压缩法(SR 法)。 其按照点估计不变原理逐次对试验数据进行压缩, 直至所有子系统的试验数据被压缩为一组数据,即为系统的等效试验结果(n,s),具体流程见文献[3]。
同样, 对于无失效数据的子系统,SR 法也不能考虑其失效的可能性,所得系统可靠度置信下限可能冒进。此外, 当子系统个数较多时,SR 法在逐级压缩的过程中会使得试验信息丢失过多[3]。
3.2 成败型并联系统可靠度置信下限计算方法
传统的成败型并联系统可靠性评估方法包括LR 法,AWI 法,ML 法和AO 法等,这些均为近似方法,有时误差较大。文献[4]通过大量的对比计算认为LR 法和AO 法较另外两者稍好, 但是当某个子系统的试验结果为无失效数据时,LR 法和AO 法均不能计算, 这极大地限制了其适用范围。为此,文献[6]提出了一种子系统失效数的近似方法,然而当子系统个数和试验数均较小时,该近似方法求得的失效数比试验总次数还大,显然错误。
3.3 非成败型系统可靠度置信下限计算方法
除成败型二项分布外,工程实际中子系统(或部件、单元)的试验结果可能服从对数正态分布、Weibull 分布、指数分布等多种类型,对此,工程上常采用点估计下限折算法,二阶矩折算法、双置信度下限折算法等折合方法[7],将非成败型试验结果转化为成败型试验结果, 再按照成败型系统计算可靠度置信下限。
由于所用折算方法的不同、 以及同种折算方法中参数选取的不同, 常常导致同一组数据的折算结果不尽相同,人为因素较大。此外,当某个子系统的可靠度较高时,其折算后的结果可能为无失效数据, 使得该部分对系统可靠度评估结果没有任何贡献,甚至无法计算。
4 对比算例
设某系统由两个相互独立的子系统串联构成, 子系统1 的试验结果为:n1=100,s1=99; 子系统2 的试验结果为:n2=100,s2=100。给定置信水平γ=0.9,分别使用LM 法、MML 法、SR 法和本文方法计算系统可靠度单侧置信下限,结果汇总于表1。

表1 系统可靠度置信下限计算结果对比(γ=0.9)
从表1 可以看出,LM 法、MML 法和SR 法给出的系统可靠度置信下限均与子系统1 的可靠度置信下限相同,这等于没有考虑子系统2 的失效可能性(其可靠度置信下限仅为0.977,实际上存在失效的可能性),导致整个系统可靠性评估结果偏于危险。 而本文方法则能同时考虑各个子系统失效的可能性,很好地解决了上述问题。
5 结论
建立了串(并)联系统可靠度(不可靠度)置信下(上)限干涉模型,给出其置信度计算方法。 在此基础上,严格证明了串联系统置信水平为γ 的可靠度单侧置信下限等于各子系统置信水平为γ 的可靠度单侧置信下限的乘积, 并联系统置信水平为γ 的不可靠度单侧置信上限等于各子系统置信水平为γ 的不可靠度单侧置信上限的乘积,从而解决了这一长期悬而未决的难题。
对于串并联系统和并串联系统,可以采用本文方法,分别通过先串联再并联或先并联再串联的方式计算系统可靠度的置信下限。
讨论了传统串并联系统可靠度置信下限计算方法存在的问题,指出计算串联系统可靠度置信下限的LM 法、MML 法、SR 法和计算并联系统可靠度置信下限的LR法、AO 法都无法考虑无失效数据子系统的失效可能性,这导致整个系统可靠度置信下限误差较大。 而本文方法则很好地解决了上述问题,且计算简单,便于工程应用。
