基于FM-EEMD 信号分解的站线变关系识别

喻 旻，余仁山，林志刚，宋志成

（国网江西省电力有限公司鹰潭供电分公司，江西 鹰潭335000）

随着城市建设步伐不断推进，城市中的配电网不断扩张，电网线路结构日趋复杂[1]。 由于配电网频繁转供、 负载的接入及线路检修等原因， 使得现有的站-线-变-支-箱-表的隶属关系一直处于频繁的变更异动中，依赖人工巡线确定站线变关系的方式效率低下、工作量繁重，已不能满足要求。除人工梳理外，还可以通过工频畸变技术、大数据分析技术等进行站线变关系的技术识别。当前主要的分析方法是通过对海量的电网数据分析来确定配电网的线变归属关系[2-5]，这种方法对于数据的要求非常高，且数据分析的准确度待考证。根据10 kV 中压载波技术的特征信号耦合法准确率高、对电网的伤害小的特点，可通过在低压侧注入特定频率的载波信号， 并检测分析中压侧各出线载波信号的强度、相位关系及编码序列等特征来确定线-变归属关系。 线-变关系识别原理图如图1 所示。

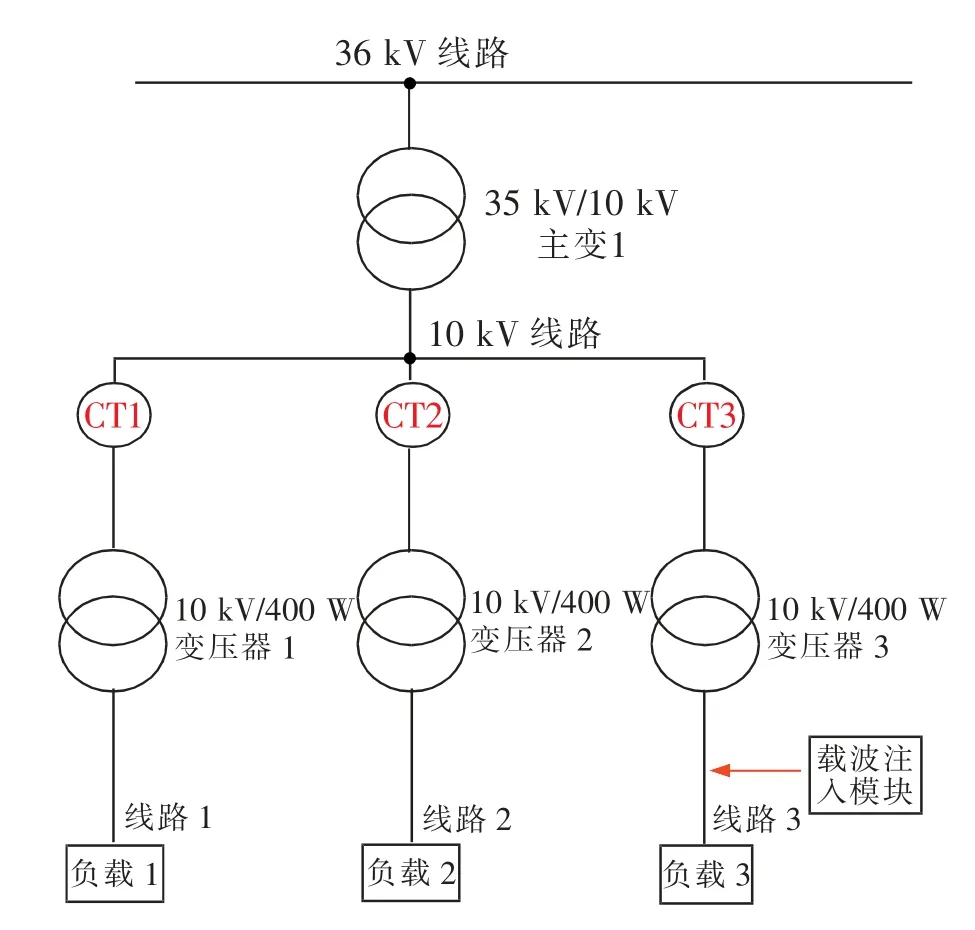
图1 线变关系识别原理图Fig.1 Schematic diagram of line-transformer relationship distinction

目前信号分析的主要方法有离散傅里叶变换（discrete Fourier transformation，DFT）、短时傅里叶变换（short-time Fourier transformation，STFT）、小波变换、希尔伯特-黄变换（hilbert-huang transform, HHT）等方法。实际工程中处理的信号基本是非平稳信号， 其特点是信号的频率是时变的，上述方法对于这类信号的处理效果均不理想。根据非平稳信号的特点，Huang 于1998 年提出Hilbert-Huang 变换[6]，Huang 创造性的提出了经验模态分解（empirical mode decomposition，EMD）算法，该方法将信号分解成多个调幅信号，这些调幅信号称为固有模态函数（intrinsic mode function，IMF）。当一个IMF 中包含一个以上的尺度的成分，或者说一个IMF 中出现多种频率的信号，这便是模态混叠现象，该现象经常发生在EMD 的结果当中。 其主要原因是受间断事件的存在及密集模态的影响，造成IMF 存在模态混叠的现象[7-9,15-16]。 为抑制间断事件的影响，文献[10-12]提出总体平均经验模态分解（ensemble empirical mode decomposition，EEMD）算法；文献[13-14]通过改进掩蔽信号等方式解决密集模态信号的影响。

由于噪声存在于信号测量过程中，使得实际测量的信号包含大量噪声，这导致密集模态信号成分和间断事件的信号成分同时存在。 当前的方法往往只能考虑上述两种信号成分中的一种情况。 综合信号调频对于密集模态信号拥有良好的解决能力和EEMD 对间断事件的抑制能力，本文改进了EMD 算法，创造性地将EEMD 与信号调频（frequency modulation，FM）相结合。 对低频成分的模态混叠现象具有良好的抑制作用。

1 EMD 及EEMD 算法原理

1.1 EMD 算法基本原理

任意的信号可以通过EMD 算法分解为一系列具有真实意义的IMF， 其基本思想是将多种频率的信号叠加的信号分解为一系列具有单一频率的波，其中最后的波我们称之为残波或者余项。 EMD 算法分解数据的本质是由数据的特征时间尺度获得本征波动模式。这个过程可形象的称之为“筛选（sifting）”过程。在引入EMD 分解过程之前，首先介绍IMF 的特点：①一个IMF 的极值点数目和过零点数目相差不大于1；②IMF的上下包络线均值为0。

对于给定信号的EMD 分解的步骤如下：

1） 寻找原始信号的极值点，并分别对极大值和极小值采用插值拟合的方法获得上下包络线eU（t）和eL（t），计算上下包络线的平均值

2） 假设待分解的原始信号为r（t），用原信号x（t）减去包络线平均值avg（t）得到疑似IMF 分量h（t），即h（t）=x（t）-avg（t）；

3） 判断h（t）是否满足IMF 的两个特点，若不满足，则将h（t）作为原信号继续重复上述过程；若满足条件，则原信号的IMF 分量为ci（t）=h（t）；

4） 用原信号x（t）减去ci（t），得到一个新信号r（t），其中r（t）相当于x（t）滤除了高频成分的信号。 并将r（t）当作新的原始信号，若r（t）是单调函数则结束，否则重复步骤1）～3）。

最终，我们可以得到原始信号x（t）的表达式

即原始信号序列由n 个IMF 分量ci（t）和一个残差r（t）组成。

对于EMD 的分解过程如何停止通常有两个判断依据，分别为：①给定IMF 幅值的最大值，当其幅值小于给定阈值，或者余项r（t）的幅值小于允许地最大值，就停止EMD 过程；②当余项r（t）是单调函数或者是常数即可停止分解。 Huang 把标准偏差系数作为分解停止的判断依据，设η 为标准偏差系数，则

式中：hk-1（t）和hk（t）分别为前一阶的分解结果和本阶的分解结果；T 为信号的总时间长度。η 值越小，所得到的IMF 分量的稳定性和线性就越好，通常η 的值在0.2～0.3 之间。

对于EMD 过程停止的判断依据的选择需谨慎，若判断依据太严格，会使最后几层的IMF 失去其实际物理意义，且占用计算资源；若停止条件过于宽松，则会造成有用信息的丢失。当一个IMF 中包含一个以上的尺度的成分， 或者说一个IMF 中出现多种频率的信号， 这便是模态混叠现象。 主要原因有两个，首先是信号成分过于复杂；再者就是EMD 对于征时间尺度不明显的信号分解能力一般，即算法本身具有一定的缺陷。

1.2 EEMD 的基本原理

由于EMD 对于征时间尺度不明显的信号分解能力一般，Huang 提出了一种通过添加白噪声，改变原始信号的特征时间尺度，使之分布在合适的尺度之上。由于白噪声具有零均值的统计特性，为消除添加的白噪声的影响，需要多次添加噪声并进行平均，最终平均的结果几位分解的结果。

对于给定信号的EEMD 分解的步骤如下：

1） 原始信号x（t）中加入的白噪声信号δ（t），得到新的信号X（t）＝x（t）＋δ（t）；

2） 将第一步得到的信号X（t）作EMD 分解，得到各阶IMF 分量和一个余项

3） 重复上述步骤1）～2）；

4） 将1）～3）得到的IMF 做集成平均处理作为最终结果；

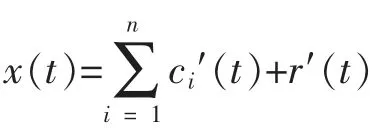
EEMD 可以重新分布信号的特征时间尺度，弥补EMD 算法的不足，可以更好的解决模态混叠的问题。而EEMD 过程中需要多次添加白噪声改变原信号的特征时间尺度的分布，因而添加白噪声的次数及每次添加白噪声的大小十分重要。 所需要添加的白噪声不仅要符合正态分布特性，且不能改变高频成分的特征时间尺度（即极值点）的分布还需改变低频成分的特征时间尺度的分布；为降低最终分解结果中白噪声的影响，白噪声的添加次数越多越好。

Huang 等给出了EEMD 算法添加白噪声的次数满足如下条件[11]

或者

式中：N 为白噪声的添加次数；α 为信号添加的白噪声和原始信号二者的幅值标准差比值；x（t）为信号分解所能允许的相对误差，即分解的IMF 重构后的信号与原始信号所允许的误差。经大量实验证明，添加白噪声的次数N 在100～300 之间，可以使白噪声对IMF 的干扰很小，同时能在一定程度上抑制模态混叠现象。

2 密集模态及信号调频

由于实际信号中不同成分的信号频率接近，传统的EEMD(或EMD)算法不能将不同频率成分的信号正确分离，称之为密集模态信号。 考虑如下信号

将上述信号x（t）进行和差化积，可将信号x（t）可转换为部分调幅信号。 信号中包含两个正弦信号时，待分解信号的EMD 分解的可行性与各阶模态信号的幅度比、频率比有很大的关系[15]，下面将给出两个信号可以从x（t）中由EMD 正确分离的条件

当混合信号满足上式的要求时，EMD 可将两种频率的信号可以分别分解到不同阶次的IMF 中。

当两种信号的幅度比满足a1f1＜a2f2，f2＜ f1且f2/f1＜0.5 时，如果可以找到一个频率f0使得下式成立

且满足a1（f1－f0）＜a2（f2－f0），则经过频率调制的混合信号依然可以正确分解。 下面介绍FM-EEMD 的分解过程，其步骤如下：

1） 将密集模态信号z（t）=x（t）+iH［x（t）］进行Hilbert 变换，得到x（t）的解析信号z（t）

2） 对z（t）作调频变换计算其解析信号Z（t），即将z（t）乘以e-i2πf0t，其中f0为选择合适的调频频率，获得的解析信号Z（t）如下

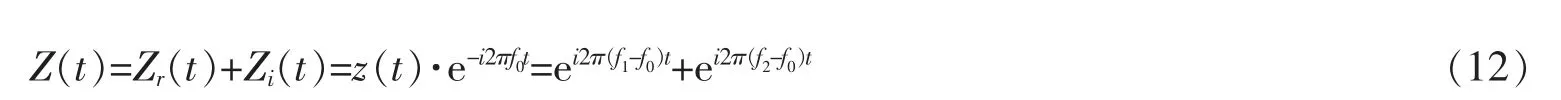
3） 对Z（t）的实部Zr（t）和虚部Zi（t）分别通过EEMD 进行分解

式中：crk（t），cik（t）分别Zr（t），Zi（t）的各阶IMF 分量；rnr，rni为相对应的余项。

4） 将上述式（13），式（14）代入式（12）得

5） 将Zr（t）乘以ei2πf0t进行调频逆变换得到x（t）

取z（t）得实部为原始信号x（t），即x（t）=Re［z（t）］。

信号调频过程中，调频频率的选择至关重要，使得调频后的信号频率比和幅值比满足密集模态信号分离的条件（式（8））。

3 仿真验证

线变关系识别仪通过在低压侧每隔0.2 s 注入频率为30 Hz 的载波信号， 图2 为截取的其中1 s 的电流数据的波形，对图2 中的数据波形分别通过EEMD 算法和FM-EEMD 算法进行处理，其中FM-EEMD 的处理过程中f0＝22 Hz，噪声标准差为0.2，加噪声次数为200 次，各阶IMF 及其频谱如图3，图4 所示：

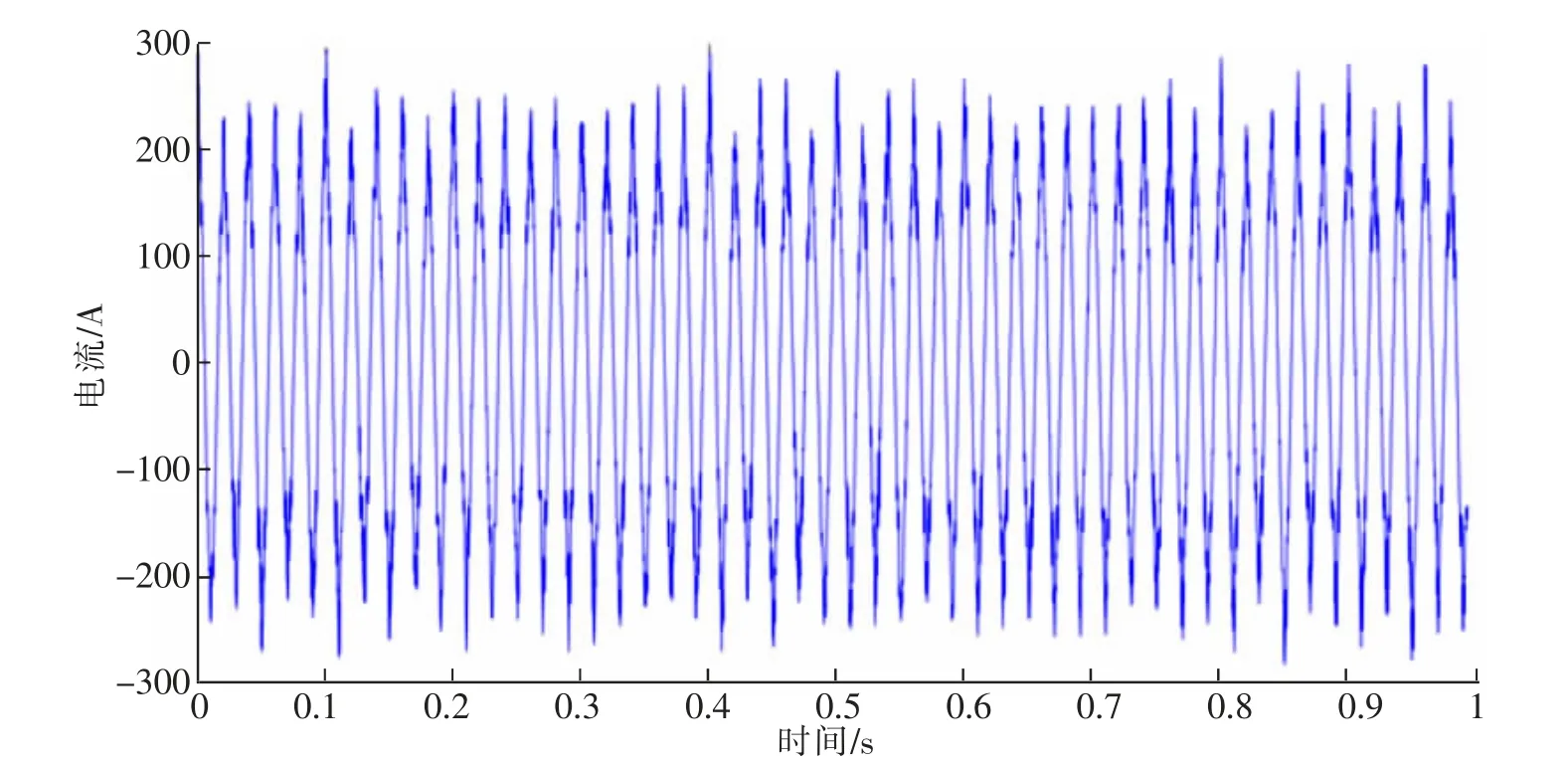
图2 线变关系识别中压侧实验信号Fig.2 The signal at medium-voltage side of line-transformer relationship distinction

图3 EEMD 分解Fig.3 EEMD decomposition

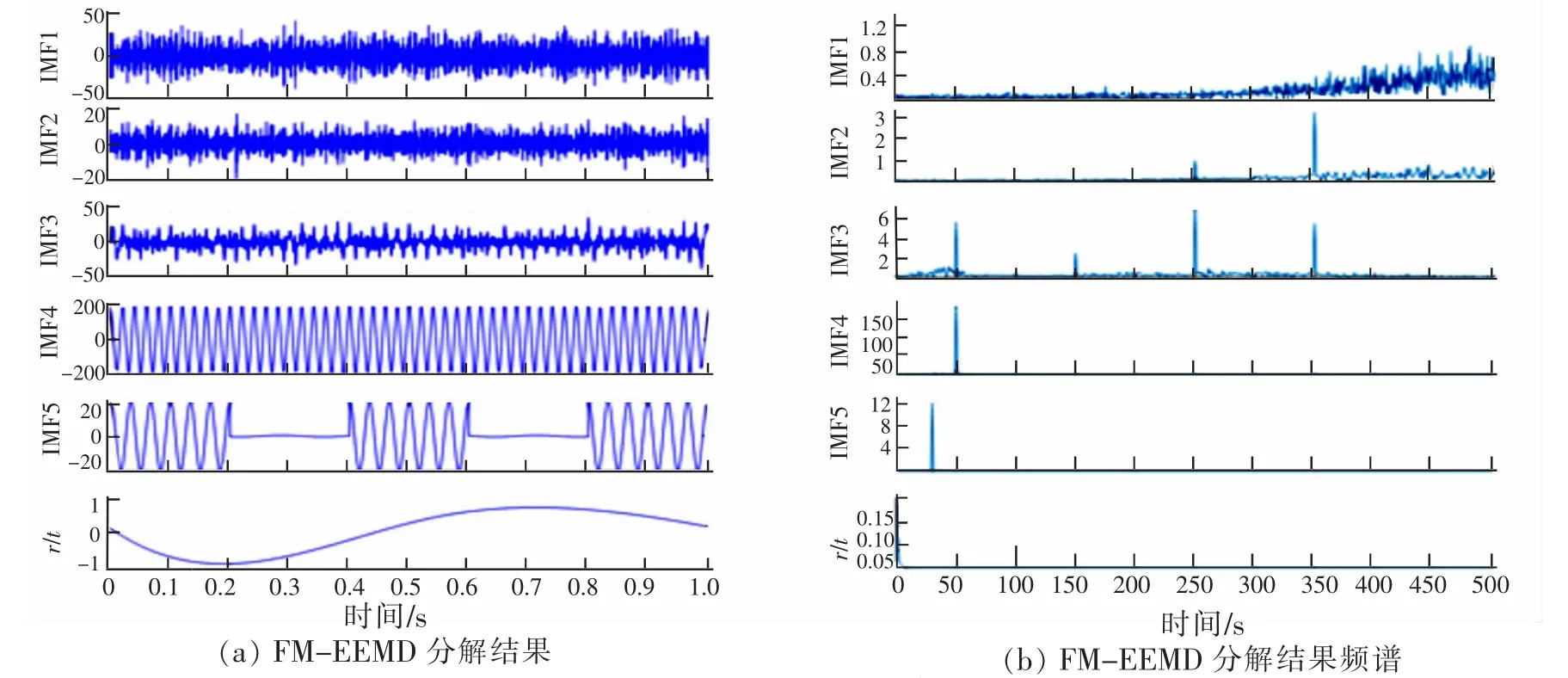
图4 FM-EEMD 分解Fig.4 FM-EEMD decomposition

分析对比图3，图4 可知，不论是EEMD 算法还是FM-EEMD 算法，信号的高频分量集中于最初的几层IMF 之中，且伴有模态混叠现象；对比图3，图4 中的IMF5 可知，经过EEMD 算法处理后的低频分量中存在两种频率的信号成分，即发生了模态混叠效应，而经过调频后得到的低频分量中不存此种现象。通过对比我们可以看出，使用FM-EEMD 对电流信号进行分解能够很好的分解出我们想要获得的载波信号的波形。

4 结论

针对EEMD 对于密集模态信号的分解过程中的模态混叠问题， 本文将EEMD 分解与信号调频进行结合，提出了能够有效抑制模态混叠的FM-EEMD 分解算法，并运用该算法对线变关系识别中的载波信号进行提取，仿真结果验证了本文所提出的基于FM-EEMD 分解算法的有效性。