第一性原理计算Ti3GeC2的电子结构与热力学性质*

2020-03-08张钰莹董兰静朱春城

哈尔滨师范大学自然科学学报 2020年4期

张钰莹，董兰静，王雪，朱春城

(哈尔滨师范大学)

0 引言

近年来，因三元层状陶瓷同时兼备了陶瓷和金属的特点，所以有关的材料模拟计算发展越来越多，其中与材料相关的电子结构与热力学性质的研究也已经成为材料研究的热点内容[1-5].但这些模拟计算研究中，主要针对的是三元层状陶瓷MAX相中的211相居多[6]，而该文采用计算机模拟的方法对MAX相中的312相的Ti3GeC2的电子结构和热力学性质进行理论研究分析.Ti3GeC2最早是由Barsoum[7]合成出来的，胡洁琼在其论文中采用对比研究的方法与其他312 MAX相做了对比研究[8].实验测得Ti3GeC2其晶格常数a=0.307nm，c=1.776nm，同时兼具金属和陶瓷的双重特性.对于MAX相化合物来说，电子结构和热力学性质决定它的许多性质，所以研究它的这些性能对探究新型三元陶瓷的研发与应用有重要的指导作用.该文采用密度泛函理论以及第一性原理计算方法，研究并计算了Ti3GeC2材料的电子结构与热力学性质.

1 计算方法与理论模型

1.1 计算方法

该文基于密度泛函理论Materials Studio 8.0软件下的CASTEP[9]模块进行第一原理性计算.原子之间的交换关联作用分别采用局域密度近似(LDA)CA-PZ泛函[10-11]和广义梯度近似(GGA)PBE泛函[12]进行近似处理,确定平面波动截断能Ecut=450eV, Monkhorst-Pack布里渊区K点取样值为13×13×2.

1.2 理论模型

Ti3GeC2的空间结构为六方晶系，空间群P63/mmc，群号为194，晶格参数为a=0.307nm,c=1.776nm,在Wyckoff的位置中，钛原子位于2a(0，0，0)，4f(2/3，1/3，0.129)；锗原子位于2b(0，0，1/4)；碳原子位于(1/3，2/3，0.069).

2 结果与讨论

2.1 电子性质

2.1.1 能带结构

晶体的稳定结构由两个晶格常数a和c以及内部参数c定义.该文晶胞参数a和c采用计算结果更为准确的广义梯度近似法确定，且后续计算也是同样近似方法.结构几何优化后，Ti3GeC2晶体沿布里渊区高对称点方向的能带结构计算结果如图1所示，从图1可更直观地看到各相能带的幅度变化和能级穿越情况.其中能量值在0 eV位置处的虚线表示费米能的位置.费米能级以上为导带，费米能级以下为价带，由图1可知，Ti3GeC2晶体的导带和价带在费米能级处重叠，此外，费米能级有穿过H-K和M-L两个能带，表现出很强的金属特性[13].图1中无明显的带隙，所以电子很容易获得能量跃迁至导带而导电；同时图1中还可以发现，Ti3GeC2晶体在H-K和M-L分布的能量并不对称，说明Ti2GeC晶体的导电性为各向异性.Ti3GeC2晶体价带基本都位于-13 ～ 0 eV区域，能带较宽，即在能带图中的起伏较大，说明处于这个带中的电子有效质量比较小，非局域的程度较大，组成这条能带的原子轨道扩展性较强.不仅如此，Ti3GeC2相邻轨道之间重叠较大，表明它成键强度较强.

图1 Ti3GeC2的能带结构图

2.1.2 电子态密度

电子态密度能够反应出原子间的价键结合情况从而反映材料的结构稳定性和力学性能影响的内在机理.图2是Ti3GeC2的总态密度图和分态密度图，通过对分态密度图的分析可以推断出化合物各原子间的成键情况.

图2 Ti3GeC2的总态密度与分态密度图

从Ti3GeC2的分态密度图可以看出，费米能级处的电子态密度计算值均不为零，说明它具有良好的金属特性.Ti的3d电子主要位于-6.0 ～ 4.0 eV能量区间，Ge的4s电子主要位于-12.2 ～-6.5 eV能量区间, Ge的4p电子主要位于-6.1 ～ 2.9 eV能量之间；C的2s电子主要集中在-11.0 ～-8.5 eV能量之间，C的2p电子主要集中在-6.0 ～-1.5 eV能量之间.

对比图2中总态密度图和分态密度图可以看出，费米能级以下，在-6 ～-1.5 eV能量之间，Ge的4p轨道电子和C的2p轨道电子分别与Ti的3d轨道电子形成的Ti—Ge、Ti—C键占主导地位；在-12 ～-9.5 eV能量区间，C的2s轨道电子与Ge的4s轨道电子形成的Ge—C键占主导地位；费米能级以上，在0 ～ 3 eV能量区间，Ge的4s电子和4p电子分别与Ti的3d电子之间分别存在轨道杂化形成Ti-Ge键占主导地位.

Ti的3d电子在费米能级处的态密度峰值为2.13，明显高于Ge和C的电子态密度峰值，由此说明Ti3GeC2的高电导率主要是由Ti的3d电子态主导.因此，费米能级以上，Ti的3d电子占据主导地位，Ge的4p电子和C的2p电子有少量贡献；费米能级以下，Ti的3d轨道电子、C的2s，2p轨道电子和Ge的4p，4s轨道电子之间相互杂化形成了较强的共价键.

2.2 弹性性质

为了了解Ti3GeC2相材料的力学性能，利用CASTEP软件对Ti3GeC2晶体进行几何结构优化后，计算了Ti3GeC2晶体的相关弹性常数，计算结果见表1.因为Ti3GeC2为六方晶系，可以通过计算弹性常数来判断其力学稳定性.根据波恩和黄昆提出的六方晶系的力学稳定性需满足式(1)关系[14]：

C11>0,

C11-C12>0,

C44>0,

(1)

Ti3GeC2的弹性常数C11=361.3 > 0，C11-C12= 276.7 > 0，C44= 155.0 > 0，(C11+C12)C33-2C132=134719.9 > 0；所以可以判断Ti3GeC2晶体能够稳定存在，且有力学稳定性.

通过计算得到的弹性常数，采用Vogit-Reuss-Hill[15]近似可计算MAX相的弹性模量，公式为：

(2)

(3)

可以根据Pugh[19]的模量比来判断材料的延展性和脆性，当B/G< 1.75时，为脆性材料，反之则为延展性材料.从表1中数据可以计算出B/G=1.24< 1.75，所以Ti3GeC2为脆性材料.根据表1中数据还可知Ti3GeC2的σ=0.182，而泊松比在-1～0.5，说明该物质具有力学稳定性[19]，所以再一次说明了Ti3GeC2的稳定性很好.与此同时，还可以从表1中看出Ti3GeC2的B值较大，说明Ti3GeC2有很强的抗体积变化特性，而且其G值也较大，说明Ti3GeC2原子间的方向价键比较明显.从表1中还可以看出Ti3GeC2晶体的E值和泊松比(σ)也较好，说明它的拉伸弹性也很好.所以综合来看，Ti3GeC2具有较高的弹性模量，质地偏脆，原子间结合力和晶体的强度都较大，材料不容易变形.

表1 Ti3GeC2晶体的相关弹性系数

2.3 晶格动力学性质

该文计算了Ti3GeC2晶体的声子色散曲线与声子态密度，从而研究Ti3GeC2晶体的热力学性质，计算结果如图3、图4所示，声子色散曲线和声子态密度[20]均可研究晶体的本征稳定性，并以此为基础计算出晶体的热力学性质.

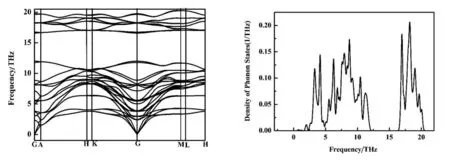
图3 Ti3GeC2的声子色散曲线图图4 Ti3GeC2的声子总态密度图

图3反映了沿着布里渊区对称点的声子振动频率变化，横坐标为连接起来的布里渊区对称点，纵坐标为经过路径的点的声子振动频率.从图3中可以看出，Ti3GeC2晶体存在声子带隙，且图中声子散射频率都在0点以上，无虚频出现，说明Ti3GeC2晶体结构稳定.声子色散图中，平缓的带对应于声子态密度的峰，说明晶格振动表现出明显局域化特征(声子频率沿着高对称点的方向变化不大).同时在图3中看到，光学分支在G点附近的绳子频率不同，说明Ti3GeC2晶体存在离子键.是因为在离子晶体中，长光学波会产生极化磁场，增加纵波的恢复能力，从而使纵波的频率提高，因此，在声子色散曲线图中出现了G点附近光学分支的声子频率不同的现象；在图3可以看到在H-K和M-L区间有平面，对应于声子态密度图中的两个最高峰值.由图4中可知，Ti3GeC2在18THz处声子态密度最大，晶格振动最强烈.

2.4 热力学性质

在得到声子色散曲线与声子态密度的基础上，该文计算了Ti3GeC2晶体的焓、熵、自由能变化关、德拜温度以及热容随温度变化的曲线分别如图5～7所示.

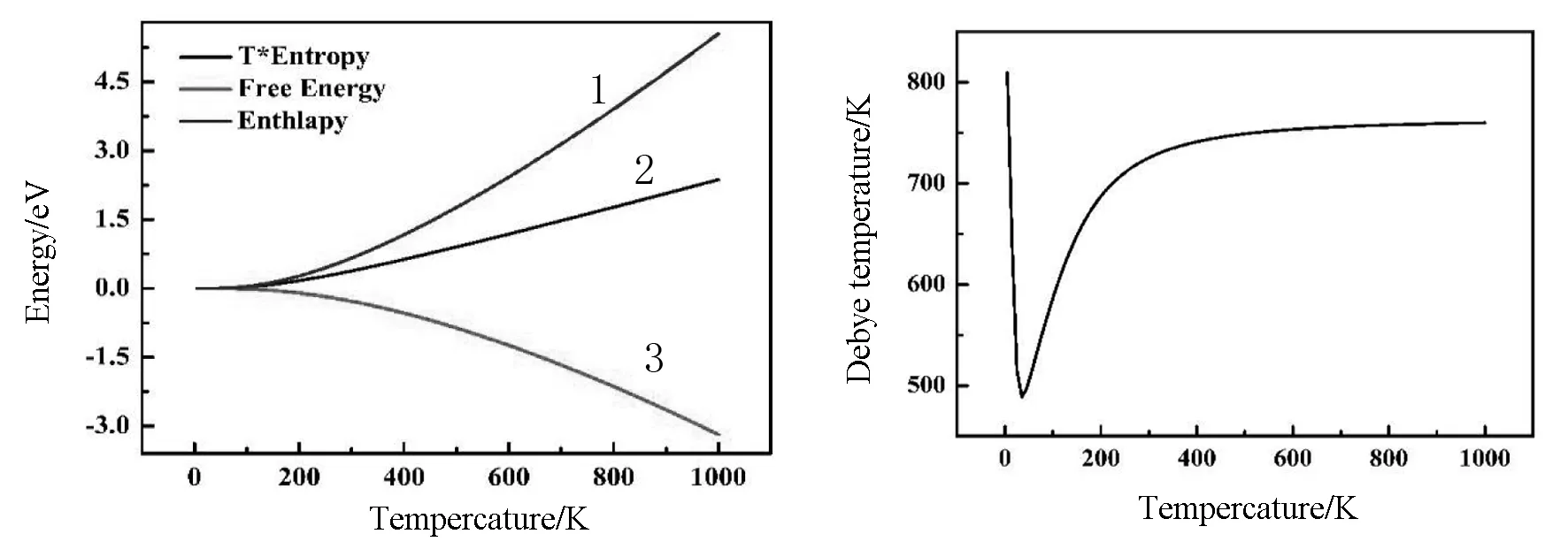
图5 Ti3GeC2能量随温度变化曲线图6 Ti3GeC2的德拜温度随温度的变化曲线

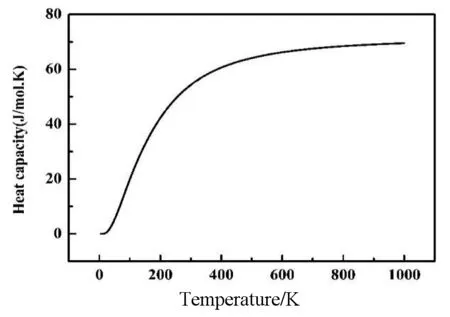
图7 热容量随温度变化的曲线

如图5所示，曲线1是Ti2GeC晶体的熵S与温度T相乘的结果，随着温度的增加，晶体中的热运动也在增加，粒子动能变大，晶体内能增加，说明晶体内粒子运动的无序度在增加，因此熵也随温度的增加而增加，故TS的乘积也随之增加.曲线2是焓H与温度T的关系曲线，H=U+pV，当温度升高时，U与pV同时在增加，也因此体系的H也随着T的增加而增加.曲线3是自由能F与温度T的关系曲线，自由能可表示为F=U-TS，此式中U为体系内能，随着温度的升高，内能和熵都在增加，但是TS的增加速度要远快于U增加的速度，所以F随T的增加而减小.

德拜温度是一个固体材料的重要物理量，它能够反应原子间结合力.如图6所示，当温度远低于德拜温度时，等容热容遵循量子规律，与热力学温度的三次方成正比，随温度的减小而迅速减小，符合德拜T3定律；当温度高于德拜温度时，等容热容CV遵循杜隆-珀替原理定律，即是一个与构成物质无关的常量，CV=3R，此时Ti2GeC的等容热容CV为常数.所以Ti2GeC晶体的德拜温度虽然随温度变化，但是在任何情况下都服从热力学第三定律和杜隆-珀替定律.

由图7可知，当温度小于700 K时，定容热容随温度的升高而增加较快，是因为在常温下，晶格热振动能量对固体的热容也有贡献；从晶格热振动角度来看，热容反映了晶体温度与格波的关系，当温度T升高时，各个格波对应的平均声子数也随之增大，同时，叠加的电子热运动能量对固体的热容也都有贡献，所以在温度较低时热容随温度增加明显；而此后曲线变缓慢是因为当温度较高时，电子的热运动能量对热容的贡献可忽略不计.