基于随机森林算法的边坡稳定性预测

2020-03-08姜泓任董庆波姜相松罗国成

现代计算机 2020年36期

姜泓任，董庆波，姜相松，罗国成

（1.大连海事大学轮机工程学院，大连116026；2.中铁建大桥工程局集团第一工程有限公司，大连116033）

近年来，边坡相关工程在我国迅速发展，而对于边坡稳定性的评估与预测是边坡工程安全性的保障，也是边坡工程的重中之重。因此，对边坡工程的稳定性进行及时有效的预测有着重要意义。为了解决非线性边坡系统的复杂性，建立随机森林边坡稳定性预测模型。选取边坡土体重度、边坡高度、孔压值、黏聚力、内摩擦角以及边坡倾角6个特征作为随机森林的输入特征向量组成元素；安全系数作为随机森林的输出。对实际数据的训练预测结果表明，模型的决定系数接近于1，回归效果好，对于边坡的稳定性预测准确。研究结果证明随机森林边坡稳定性模型的可行性。

边坡工程；随机森林；机器学习；稳定性

0 引言

随着我国经济发展以及基础的建设，道路桥梁工程、矿山建设工程、水利工程等工程发展迅速，其中存在着大量与边坡相关的工程。边坡的稳定性事关重大，一旦出现滑坡灾害，会严重危害到人们的人身安全以及国家财产。因此，找到一种准确且便捷的道路边坡稳定性预测方法便显得尤为重要。

边坡稳定性受到多个因素影响，在实际的边坡工程中，各个影响因素相互作用，组成一个复杂的非线性系统。长期以来，研究者们在预测边坡稳定性时，往往采用将影响边坡稳定性的因素量化后带入物理模型进行分析这一传统方法。例如肖欢等人[1]采用极限平衡法分析矿山的局部边坡稳定性；年庚乾等人[2]利用双重介质模型对裂隙岩质边坡的渗流及稳定性进行分析；彭超等人[3]将基于张拉剪切复合破坏的强度折减法应用于边坡稳定性分析。然而由于边坡系统的复杂性，建立的物理模型不仅复杂，还可能对实际情况的反应有所偏颇，因此其对于稳定性预测的准确程度相对不足。而近年来机器学习算法的兴起很好地弥补了传统物理模型的不足。

机器学习的核心目的是使机器能从大量数据中寻找学习规律，并将获得的学习规律应用到其他的同类数据中[4]，无需建立具体的物理模型，可以较好地预测非线性复杂系统。迄今为止，已经有很多研究人员将岩土学科与机器学习算法相结合，建立边坡稳定性预测模型。例如，何永波等人[5]将通过卷积神经网络建立了边坡稳定性分析模型；牛鹏飞等人[6]利用PCA-LMBP神经网络建立了边坡稳定性预测模型；黎玺克[7]采用了遗传算法改进BP神经网络建立了边坡稳定性预测模型。相较于其他机器学习算法，随机森林具有更好的泛化性以及准确性，且计算量更少，在训练集样本分布不均以及解决非线性回归问题中有着更好的表现。

笔者随机抽取某组边坡样本数据中的一部分作为训练集建立了基于随机森林算法的边坡稳定性预测模型，并对剩余部分数据进行了预测与分析，为道路边坡稳定性预测提供了一种新的机器学习算法模型思路。

1 随机森林模型基本原理

1.1 随机森林的特点

随机森林是一种以决策树为基学习器的有监督的集成学习算法。集成学习是一种十分重要且实用的机器学习方法，随机森林算法便是集成学习算法中的典型算法之一，它以简单而且高效的特点为人所知。在随机森林模型中，包含着多个由Bagging集成算法训练的决策树，当待计算样本输入后，模型通过集成众多决策树的输出结果并以投票的方式输出结果。随机森林预测模型可分为两类，一类是回归模型，另一类是分类模型。两者的区别在于预测结果的性质：前者预测结果为具体数值，后者预测结果为划分的类别。本文所采用的边坡稳定性预测算法为随机森林的回归算法，通过边坡的几项特征对于边坡安全系数进行回归预测。在随机森林的回归模型中，集成算法为Bagging系列算法，基学习器采用的为CART回归树模型。

1.2 Bagging系列算法

Bagging系列算法[8]是一种并行的集成学习算法，它的提出是为了处理数据的不平衡问题，能够有效地增强回归器的回归效果。在Bagging算法中，基学习器的训练集是通过对原始样本进行随机抽样得到的。假设原始样本总数为M，对其进行N组取样。每组取样为有放回的随机取样，样本容量也为M。从而得到N组采样集，将这N个采样集分别进行独立训练，可得N个基学习器，将N个基学习器通过集合策略即可得到通过Bagging算法抽样的强学习器。原始样本集中每个样本未被抽中的概率为，当M足够大时，概率趋近为，约为36.8%[9]，这说明了每次抽样原始样本集中约有1/3的样本没有被抽中，这可以有效地增加模型对噪声的容忍度，适和应用于一些稳定性差或倾向于过拟合的模型，如决策树模型。

1.3 CART决策树的建立

CART决策树是一种基本树模型，广泛应用于各类树模型中，其特点是既能处理分类问题也能处理回归问题。所谓回归，即根据输入的特征向量决定对应的输出值，在CART回归树结构中，特征空间被划分成了若干单元，每个单元对应着一个输出值，因其为二叉树结构，特征节点处的取值只有“是”与“否”。对于训练集数据，需找出每个特征的最佳划分点以及对于不同的特征划分的先后顺序，再根据其特征在每个特征节点处进行判断，按照其特征将其划分到某个单元，便能得到对应的输出值。

在寻找最佳特征划分点时，使用最小化均方差法。假设X和Y分别为输入和输出变量，并且Y是连续变量，假设训练数据集如下：

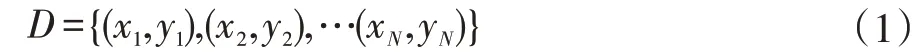
其中输入特征向量为：n为特征个数，i=1,2,…,N，N为样本容量。

在进行划分前，从特征向量中等概率随机抽取一个特征子集，在进行每一次的划分时，遍历子集中的所有特征的所有取值，选择一个使平方误差最小的点作为最优切分点。记作训练集中第j个特征变量和它的取值s，并定义两个区域：

与：

为找出最优j和s，对下式求解：

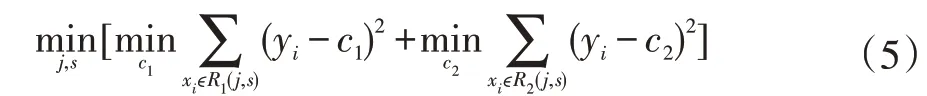
也就是找出j和s，使要划分的两个区域平方误差和最小。根据证明，c1，c2为两个区域内分别对应的Y的均值。

找到最优的切分点（j，s）后，按照最优切分点将输入空间依次划分为两个区域，接着对新生成的每个区域都重复上述划分过程，直到满足停止条件。如此，一棵回归树便被成功地构建了出来，通常称这种回归树为最小二乘回归树。

划分结束后得到的若每个叶节点上输出数值唯一则以该值作为该叶节点的预测数值，若最终叶子节点上输出数值不唯一，则以该节点上所有人的平均数值做为该叶节点的预测数值。

1.4 随机森林模型的建立

简单来说，随机森林模型是Bagging集成算法与决策树的结合。

（1）使用Bootstrapping方法，从初始数据集中随机、有放回的进行n次采样，每次采集m个样本，生成n个训练集。

（2）对n个训练集分别进行训练，得到n个决策树模型。

（3）对于每个决策树模型，按照之前所述的方法进行二分裂。

（4）将生成的多颗决策树组成随机森林。对于分类问题，按照多棵树分类器投票决定最终分类结果；对于回归问题，由多颗树预测值的均值决定最终预测结果。

2 基于随机森林边坡模型建立

2.1 数据集

为了验证基于随机森林的边坡稳定性预测模型的预测效果，引用《基于网格搜索支持向量机的边坡稳定性系数预测》[10]一文中的边坡样本数据42组。其中每组数据样本都包含特征向量以及对应的安全系数两部分，特征向量由边坡土体重度、边坡高度、孔压值、黏聚力、内摩擦角以及边坡倾角六个特征变量组成。通过随机森林预测模型对样本数据进行学习，找到边坡特征向量中六项特征值与边坡安全系数的非线性关系。具体数据样本如表1。

表1 边坡样本数据集

2.2 模型建立

从上述边坡样本中随机抽取34组样本作为训练集（样本序号1到34），剩余的8组样本作为测试集（样本序号35到42），在进行归一化处理后通过寻优方法，确定该随机森林模型决策树数量为101，在每个节点处进行分割的特征子集数量为5，然后建立随机森林边坡稳定性预测模型。

3 预测的结果与分析

3.1 评价指标

为了对随机森林边坡稳定性预测模型进行客观评估，引入决定系数（coefficient of determination）这一概念作为模型的评价标准。决定系数的数学表达式如下：

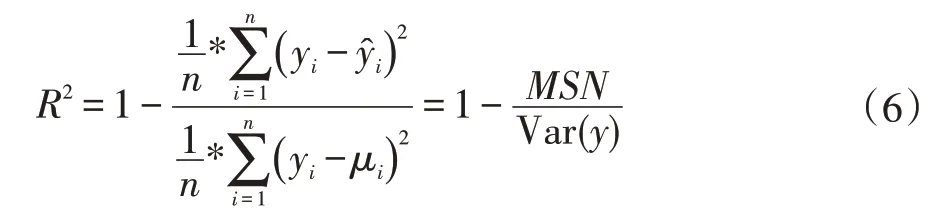
决定系数的值代表了在回归模型中，能由自变量解释的变化程度占总变化程度的比例，总变化程度即为样本的方差，不能由自变量解释的变化程度由（真实值-回归值）的平方和来表示，因此决定系数可以用1减去不能由自变量解释的变化程度占总变化程度的比例来表示，决定系数越接近1，说明预测值可以被解释的程度越高，预测结果越准确，回归模型的效果越好。

3.2 结果分析

为了体现基于随机森林的边坡稳定性预测模型相比传统机器学习算法的优势，将随机森林模型的回归及预测结果与BP神经网络的回归预测结果进行对比。

绘制随机森林的边坡稳定性模型的回归拟合曲线与BP神经网络回归拟合曲线同时与真实值进行对比，如图1所示。从图中可知，在对训练集进行回归时，与BP神经网络相比，回归森林模型所得到的结果与真实值更加的接近，并且回归效果更加稳定。通过计算，随机森林回归模型的决定系数为0.989；而BP神经回归模型的决定系数为0.936。相比之下，随机森林模型的决定系数更接近于1，拟合效果更好。接着多次抽取训练集，得到的安全系数拟合曲线都与真实值曲线接近，决定系数均与1接近，由此可得随机森林回归模型的稳定性同样良好。

两种模型对于测试集的安全系数预测拟合曲线与真实值曲线对例如图2。

两种模型对测试集预测结果对例如表2所示。

结合图2和表3可以看出，基于随机森林的边坡稳定性预测模型预测结果与BP神经网络模型相比，平均误差更小，对于边坡安全系数的预测值与真实值更加接近，预测的结果更加稳定。若将安全系数大于1视作稳定，小于1视作不稳定，随机森林边坡稳定性预测模型能够更加准确地对于边坡的稳定与否做出预测。