基于有限元的密度投影场快速求解研究

2020-03-08陈沁梅张征宇周润严华祝福顺李果阳

现代计算机 2020年36期

陈沁梅，张征宇，周润，严华，祝福顺，李果阳

（1.四川大学电子信息学院，成都610065；2.中国空气动力研究与发展中心，绵阳621000）

某流场中，密度投影场与扰动引起的光线偏移角之间满足泊松方程的关系，且该泊松方程的源项是一系列离散的偏移角，无法利用现有方法直接求解。在有限元法的基础上，利用神经网络拟合源项中偏折角与采样坐标的关系，得到剖分网格点上的源项；同时，针对神经网络的加入使得有限元法中单元载荷向量的求解过于耗时的问题，在求解源项时，论文将三角单元整体预测的二重积分表达式近似替换为三角单元结点预测的常数表达式。仿真实验表明，引入神经网络拟合偏折角，相对于传统的插值方法，可以取得更高精度的结果；而且在相同误差下，提出的算法大大提升了运算速度。将该算法应用到真实流场中，得到的该密度投影场的特性与搭建的真实环境的结果相似，进一步说明所提算法的有效性。

密度投影场；泊松方程；神经网络；有限元；二重积分

0 引言

流场中物理模型的密度投影场信息是飞行器气动外形优化的重要数据，因此流动密度投影场的定量分析一直都是流场的一个重要研究方向[1]。目前有效的方法是将背景纹影技术（Background Oriented Schlieren，BOS）光路和视频测量技术融合起来研究试验中的密度投影场，通过测量标记点光束穿过扰动流场到相机摄影中心的光偏折数据，以解决纹影和阴影技术定量化不足、干涉测量技术抗干扰能力差和波面传感器空间分辨率不够等问题[2-3]。

密度投影场在数学上是一个带有源项的泊松方程，一般使用有限元法进行求解[4]。有限元法是从变分法和有限差分的基础上发展而来的，它不但保留了有限差分的离散处理，还借鉴里兹法的试函数（即下文提到的形函数）思想[5-6]。早在上世纪四十年代就出现了有限元的计算思想，但随着高速电子计算机的出现，有限元法才得以真正用于解决工程问题。1956年Turner等人发表了第一篇有限元法在结构力学中应用的论文。1966年，Zienkiewiez等人第一次提出将有限元法应用于求解位势流问题[7]。这之后，有限元法被迅速应用到流体力学中[8]。可以认为，有限元法是流体力学中理论研究、实验分析及解决工程问题的强有力的工具。

考虑到本文所求解方程的特殊性，即常见泊松方程的源项是解析式，而本文需要求解的泊松方程源项是由一系列离散点表示，无法直接利用有限元进行求解。因此，需先拟合源项中偏移角与采样坐标x,y的关系，将其化为一般的泊松方程。传统的方法有曲面拟合和插值，但精度都比较低。由于神经网络能够以任意精度逼近连续函数，泛化能力强，显著地优于二次曲面拟合结果[9]。因此，本文采用神经网络来实现拟合。

1 密度投影场的建模

本文通过将BOS技术和视频测量技术结合的方式对密度投影场进行建模。在BOS系统中，相机的观测对象设置为具有随机点阵分布的背景，当二者之间存在流场扰动时，相机上背景点阵的像会相较于无扰动时有一定的偏移[10]。由于该偏移量与扰动流场的折射率分布直接相关，便可定量得到扰动流场的密度分布及通过扰动流场的气动光学特性信息[11-12]。

图1 BOS系统光路图

已知，BOS将待测扰动流场的密度变化与光线的偏折角联系在一起，且偏折角与气体密度存在一定关系[13]。通过搭建光路，如图1所示，可获得光线的偏折角。

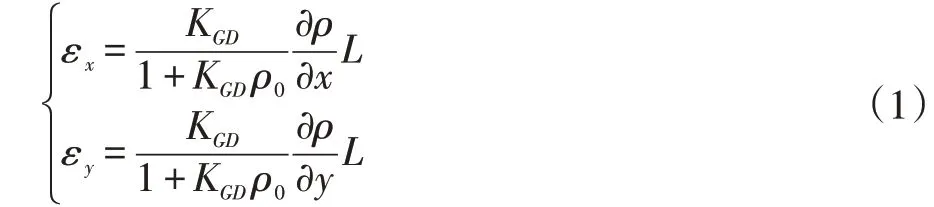
式中：空气中标准状态下，KGD的取值为0.226，单位为cm3g，ρ0为流场试验的总压。可见，经过扰动流场后，光线的偏折角与密度的梯度以及光路长度成正比，两式微分后相加，可得到如下的含有源项的泊松方程[14]。

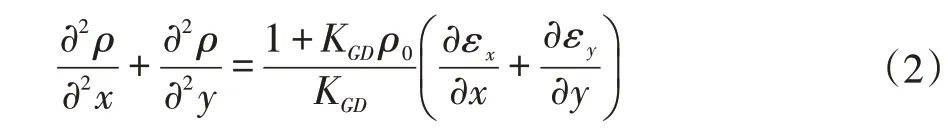
它表示密度投影场与x,y方向上偏折角的关系。而本文的目标，就是求解这一泊松方程。

2 密度投影场求解

2.1 单元剖分

为了更加准确地求解密度投影场的泊松方程，采用三角剖分将待求解区域离散化，如图2所示。剖分过程包括三个步骤：首先将待求解区域( x,y)按照一定间隔k划分成矩形网络，其次将上一步剖分好的矩形网格沿着对角线划分成一系列三角形单元；最后为每一个三角形单元和其顶点编号，为之后的循环单元求解做准备[15]。

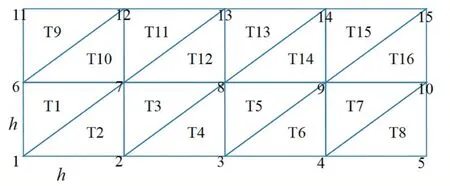
图2 三角单元图

2.2 偏移角拟合

密度投影场的泊松方程源项中偏移角与采样坐标x,y的关系的拟合是本文算法的重点。它的精确度直接关系到最终方程求解的精度。本文利用神经网络来实现拟合，得到偏移角与采样坐标x,y的关系，进而利用训练得到的网络模型预测剖分点对应的偏移角，最后由偏移角求出源项。

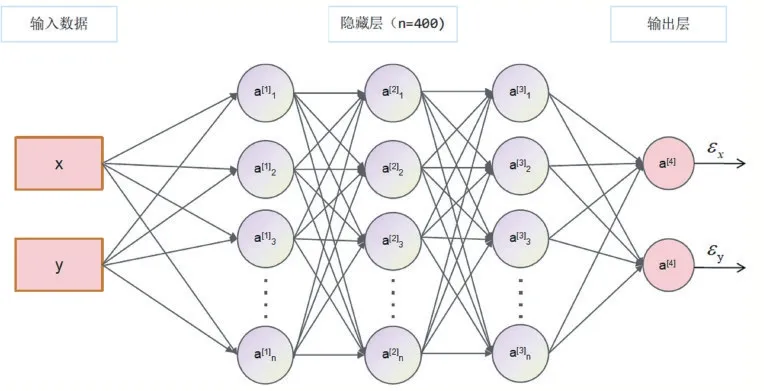
图3 神经网络结构图

出于性能和效率的考虑，本文采用一个具有三层全连接层的神经网络来拟合偏移角和采样坐标x,y的关系。网络结构图如上图3所示。首先，将数据处理得到的偏移角ε和坐标值( )x,y，作为输入，利用均方差损失约束网络，经过多次迭代，可以训练得到一个偏折角ε在x,y方向上对应于背景板坐标值的拟合网络。其中，激活函数为tanh，优化函数为Adam。网络训练完毕后，将三角网格剖分得到的坐标点输入网络，就可以预测其对应的偏移角。

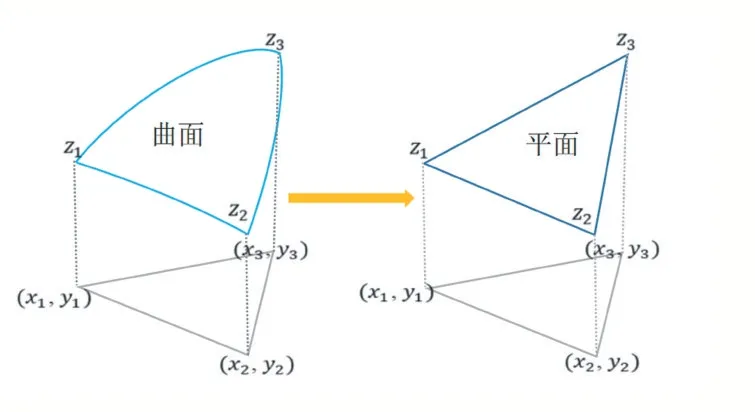
图4 三角区域的近似替代

式中：h为求解步长，其值为1 k。

2.3 方程求解

单元载荷向量的求解与泊松方程的源项有关。即对于本文而言，要求解单元载荷向量，需先预测三角单元的源项，再对其进行坐标变换，再求解如下所示二重积分：

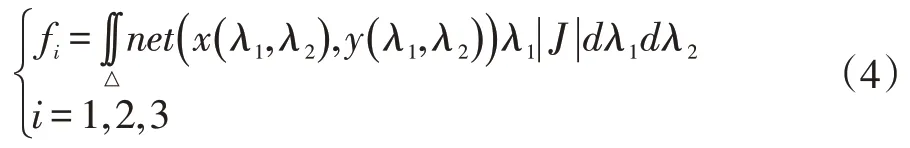
式中：fi表示一个单元上第i个形函数与源项的作用，x( λ1,λ2),y( λ1,λ2)表示单元上的点经坐标变换后的坐标，|J|表示单元变换的雅克比行列式。

显然，由于神经网络预测的加入，单元载荷向量的求解时间效率会有所下降。因此，参考定积分的几何定义，对其进行优化。

由于三角形区域较小，本文采用结点坐标确定的平面代替整个三角形单元，如图4。

即可定义一个三维平面，并用其代替三角单元预测，再对其进行二重积分得到单元载荷向量，如式（6）。

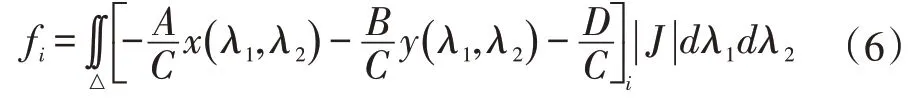
时间上，对于整个单元的源项预测，等价于预测单元上的所有点的源项，且由于一个单元上有3个形函数，需进行三次单元预测；而对于结点的源项预测，只需预测所有单元结点的源项。设每个单元需预测M个点（该点数仅与二重积分预置函数integral的运算规则，计算机性能有关，与三角单元大小无关），剖分点数为n2，则按照本文的剖分原则，剖分单元有2( n-1)2，求解使得改进前后时间性能相同时的临界剖分点数，即求解方程：

合并后，得：

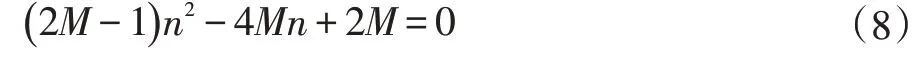
由求根公式求得其正根为：

即当结点数大于4时，改进算法均比原方法省时。

此外，当用结点预测替代单元预测后，二重积分的被积函数转为显式方程，即：

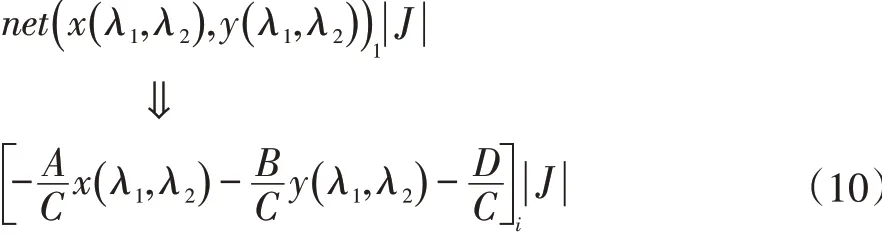
积分区域为直角三角形单元，即{(λ1,λ2)|0≤λ1≤1-λ2,0≤λ2≤1}，可利用积分公式将二重积分化为常数表达式，在保证误差不变的情况下，也可提升速度。

3 实验及结果分析

为了验证所提泊松方程解法的精度和时间性能，本文首先对比了在不同疏密的网络剖分下，神经网络与传统插值方法对同一方程源项的预测效果；再设计了两组仿真实验，利用一个已知真解的泊松方程，在不同的网格剖分精度下，分别测试了原有限元法和本文改进的有限元法的求解精度和求解时间。实验结果如表1-表3。进一步，本文也在真实的密度投影场场景下，利用BOS系统得到的数据测试了所提方法的有效性，结果如图5所示。本文实现算法的环境是MATLABR2017b以及Python 3.6.5。

3.1 插值法与神经网络法对比

为了验证相比于传统插值算法，神经网络对源项的预测更精确，本文针对泊松方程：

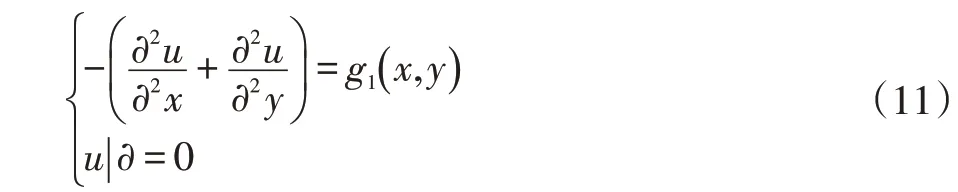
式中：Ω=( 0 ,10)2,g1( x,y)=-6x-6y，真解为u( x,y)=x3+y3。进行了不同疏密的网络剖分，从源项g1( x,y)中产生数据对( xn,yn,g1n( xn,yn))，并分出10%作为测试集，其余作为训练集。

采用L2范数进行误差估计[16]，其公式为：

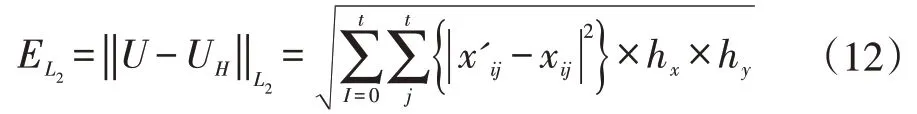
分别用插值和神经网络的方法对源项进行预测，得到如表1所示的误差结果。

从表1中可见，在取样规模较大时，随着网格剖分的精度增加，神经网络和插值方法的误差都会减小，但是在同一规模下神经网络的误差远小于插值方法的误差说明神经网络拟合精度远高于插值方法。

3.2 仿真实验

由于实际BOS系统测得的流场密度所满足的泊松方程的源项为一系列离散的点，而不是确切的解析表达式，因此无法求出泊松方程的解析解。为了验证所提解法的精度和时间性能，本文采用一个已知真解、源项为已知解析式的泊松方程

式中：Ω=( 0 ,1)2,g2( x,y)=2π2sinπx sinπy，真解为u( x,y)=sinπx sinπy。使用与实际BOS系统中相同的数据采样方式从源项g2( x,y)中产生相同数目的数据对( xn,yn,g2n( xn,yn))作为神经网络的输入，来拟合得到源项g2( x,y)与坐标点x,y之间的关系，继而利用该拟合得到的源项通过原有限元法和本文的方法求解公式（13）所示的泊松方程。

（1）误差分析

已知，在均匀网格下，结点z上的误差为：

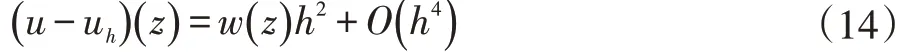
式中：u为真实解，uh是步长为h时所求近似解，w(z) h2是精度为O(h4)时的误差。若剖分间隔k扩大一倍，即h缩小一倍，则：

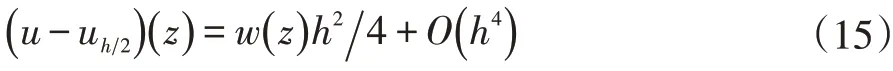
由公式（14）和公式（15）可得到h 2步长时的可计算误差为：

因此，针对不同的剖分步长h，我们对比了本文所提方法和原有限元法的可计算误差，误差对比结果如表2所示。

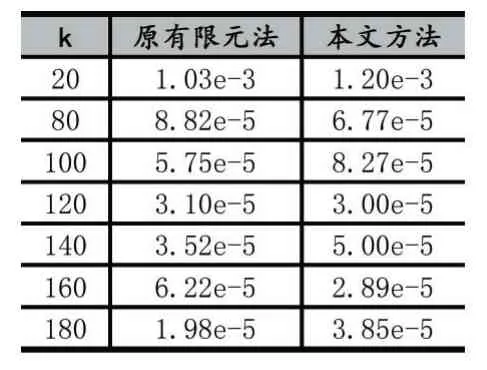
表2 误差对比

其中，两种方法不同点在于单元载荷向量求解方法不同。有限元法为对整个三角单元预测进行二重积分；而本文方法为将三角单元结点预测输入到二重积分化简的解析式中。由表2可知，剖分间隔越大，网格剖分得越密，两种方法的求解误差均越小，且随着采样数的增大，误差出现震荡，最后可认为改善剖分间隔，已对其误差的减小作用不大。

（2）时间分析

为了验证所提解法能够有效地减少离散源项的泊松方程的求解时间，本文在不同的网格剖分间隔k下测试了原有限元法和本文方法的求解时间如表3所示。

表3 时间性能

从表3可知，在实验中测试的所有的网格剖分精度下，本文所提的解法时间性能大大优于原有限元法，而且网格剖分得越细，本文所提解法的时间效率优势越明显。

结合表2和表3可看出，本文所提的解法在牺牲了很小的求解精度下可以大大提高求解的时间效率。

3.3 真实实验

图5 真实实验二维结果图

真实实验数据是某真实流场提供的。根据密度投影场模型，如图1所示，我们可以得到观测点A坐标( )x,y及有扰动时的点A＇相对无扰动时A的偏移量对应的像素值( )∆x,∆y。欲求出方程的源项，还需得到背景板上的偏移值，再将坐标值投影到扰动场中。再由式（17）的偏折角公式，就可以得到泊松方程源项中的偏移角。