关于高中物理动力学的分析研究

田兆

摘  要：高中物理动力学问题是高中物理教学中的难点，也是高考的必考考点，且占用分值较大，因此对学生来说学习好物理动力学十分重要。物理动力学也是学习高中物理的基础，学生需要着重掌握。本文从题目入手，分析解决高中物理动力学问题的方式方法，提高學生的解题能力。

关键词：高中;物理;动力学

动力学是高中物理中的主要内容，动力学主要是研究物体之间的相互作用及其对物体运动状态产生的影响。动力学是建立在牛顿的三条运动定律基础上的，即力是物体产生运动的原因、力是物体产生加速度的原因、力是物体之间相互作用的原因，在这三条运动定律的基础上，对不同的物理问题进行具体分析，解析物体本身及相互之间的受力情况。物理动力学不仅仅是高考的必考考点，最重要的是能够被应用到我们的实际生活中，对我们的生活中产生的现象进行解析。通过对动力学的学习，我们了解到了常见的几种力，包括重力、摩擦力、弹力等，通过对物体建立物理模型，进行受力分析，了解物体的运动状态。本文以实际问题出发，探索解决物理动力学问题的方式方法。

题目如下：

将一个质量为m的木块放在与水平面成β角的斜面上，二者之间的静摩擦力系数μ₀较小，若不加支持，木块将加速下滑。问须加多大的水平力F，木块能恰好不下滑？

一、审清题目，确定对象

做物理动力学问题，首先就确定研究对象，这要求学生审题清晰。高中物理涉及到的问题广泛，学生首先对问题进行通读，确定此题目属于哪一类问题。一般的动力学问题都是产生在两个物体之间的受力问题，题目中一般会表明，即使有些题目表达的比较隐晦，学生也可以通过课堂上所学的内容，锁定题目类型。其次要确定研究对象，即问题所问的物体。以本题问题，首先通过审题，题目中问到需加多大的水平力F，我们能够知道这是一道动力学问题。其次分析对象，体重有两个物体，一是质量为m的木块，一是与水平面成β角的斜面，问题问对木块施加多大的力，才能够保证木块不下滑，因此对象为木块，完成解题第一步。

二、提炼信息，建立模型

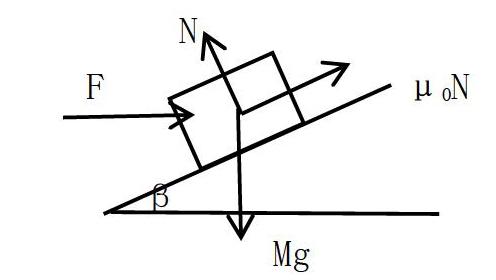
通过审题，我们已经确定了对象，其次对对象所受的力进行总结，木块受力如下图。

现在木块除受到外力F外，还受到三个力，分别是自身的重力mg，斜面给予木块的支撑力N，斜面给予木块的反摩擦力μ₀N。另外斜面水平呈β度角，这样在F力施加后，木块刚好处于静止状态，即木块受力均匀，达到平衡状态，由此建立物理模型。建立物理模型是解决物理问题的关键，通过构建物理模型，能够让问题更加清晰化，有利于学生解题，避免产生解题盲区，让解题思路更加清晰化。尤其是当学生面对复杂问题时，物理模型为学生解题提供清晰的思路，避免在解题过程中出现错误。物理模型是一种抽象化的表达形式，但是都遵循一定的物理定律，只要充分掌握物理定律，建立完整的物理模型，对学生解题有很大的帮助。

三、应用物理定律，解决问题

根据物理动力学定律，物体的运动状态与其所受力有关，物体的运动速度也受力的影响，此题中可以看做运动速度为0，此物体时受力平均，各个方向受到的力平等，也可以在物理模型中，建立坐标系，分为X、Y轴，在X轴上木块受到部分反摩擦力和部分弹力。在Y轴木块受到重力和部分弹力。由此可以列方程为：

Fcosβ+μ₀N-mgsinβ=0

N-Fsinβ-mgcosβ=0

解方程得F=（sinβ-μ₀cosβ）/（cosβ+μ₀sinβ）mg

N=mg/（cosβ+μ₀sinβ）

由此，得到使木块处于静止状态，所需的外力F大小。通过简单的问题了解解决问题的方法，在此基础上进行问题扩展，从而解决更多的物理问题。随着学生知识量的增加，物理定律增多，问题更加复杂，但是基本的解题逻辑不变，最主要的是能够建立准确的物理模型，熟记各项物理定律，准确使用。

四、活学活用，举一反三

物理动力学问题虽然形式不同，但是应用原理相似，学生只要对解题方式进行掌握，对每条物理定律熟知，学会举一反三，就能够解决更多的问题。同时，物理问题是一个大范围的问题，需要学生考虑全面，精确分析问题，找到准确的解决方法。很多学生对物理定律采用死记硬背的方式，这种非常不利于学生解题，解决为的关键就是能够快速的确认问题的种类，只有在融会贯通的基础上，才能够保证解题准确性。除此之外，学生应该活学活用、举一反三，例如，在本题中，如果问的不是木块静止所需要的力，问题是在木块处于某一均匀速度延倾斜面运动，道理是相同的，此时木块的速度a就不再为零。动力学所涉及的内容比较多，应用范围也比较广，这就要求学生能够深入研究，掌握规律。

五、总结

高中物理作为高考的一门重要学科，而动力学所占分数比例又比较大，要求学生对动力学的学习提高重视。物理是对基础要求比较高的，学生应该从易入难，掌握学习技巧，熟记定律知识，通过构建物理模型解决各类问题，深入研究方案方法，活学活用，举一反三。

参考文献

[1]  周松.不同物理情景下弹簧问题的解题思路[J].招生考试，2018（22）：49-50

[2]  韩静，代晓宇.动力学中涉及的几类问题[J].中学物理（高中），2017（33）：32-34

[3]  刘正春.解决动力学问题的核心思路[J].中学物理（高中），2018（7）：55-56