一类高效无证书签名方案的密码学分析
2020-03-07李祖猛
◆李祖猛 王 菁
(1.广东科学技术职业学院计算机工程技术学院 广东 519090;2.广州市信息工程职业学校基础部 广东510000)
2003年亚密会上Al-Riyami和Paterson[1]首次提出无证书密码系统的概念。无证书密码系统中,密钥生成中心KGC(key generation center)和用户一起完成用户的密钥生成。这种产生密钥的方式使得KGC 不能获知用户的完整私钥,从而解决了基于身份的密码体制[2]中的密钥托管问题,而且因为不再需要证书中心CA对用户的证书进行管理和维护,所以也解决了传统基于PKI 公钥密码体制[3]的证书管理问题。
无证书签名是无证书密码系统中的研究热点之一。自Al-Riyami和Paterson在文献[1]中提出第一个无证书签名方案以来,许多无证书签名方案相继被提出[4-10]。但在无证书密码系统中,因为用户的公钥没有直接认证,所以无证书密码方案容易遭受恶意用户的替换公钥攻击[11-12]。此外,无证书密码系统中,KGC 参与用户密钥的部分数据产生,且KGC 拥有主密钥,所以无证书密码方案也容易遭受恶意不诚实KGC的伪造攻击[6-13]。2016年,汤永利等人[14]基于椭圆曲线离散对数困难性假设提出了一类高效的无双线性对的无证书签名方案,该方案包括8个子签名方案,并在随机预言模型下给出了安全性证明。
本文对汤永利等人的8个无证书签名方案[14]进行密码学分析后,发现其中的第1、3、6方案不能抵抗恶意不诚实KGC攻击,其中的第2、4、5方案不能抵抗恶意用户的替换公钥攻击,其中的第7、8方案即使不替换公钥,恶意攻击者也可以利用用户的原始公钥对任意消息伪造出有效的签名。本文针对每种方案的安全漏洞分别给出了相应的伪造攻击方法,分析结论表明,文献[14]中的8个签名方案都是不安全的。
本文的组织结构如下:在第1 节中,首先介绍一些预备知识;在第2 节中,简要回顾文献[14]中的无证书签名方案;在第3 节中,对文献[14]中的8个签名方案给出伪造攻击。最后总结全文。
1 预备知识
1.1 困难问题
设E/Fp是定义在有限素域Fp(p为大素数)上的椭圆曲线,取由E/Fp上所有点和无穷原点O构成椭圆曲线的一个循环加法子群G,点P是G的一个生成元,其阶为q。
定义1 椭圆曲线离散对数问题(Elliptic Curve Discrete Logarithm Problem,ECDLP):给定G上的点Q,求,使得Q=aP。
1.2 无证书签名方案的形式化定义
在无证书签名方案中,包括3个合法参与者:KGC、签名者IDs、验签者IDv。一个无证书签名方案通常包含以下7个多项式时间算法:
(1)系统参数建立算法
由KGC 运行,输入安全参数k,输出系统公开参数params和主密钥s,s由KGC 秘密保管。
(2)部分私钥生成算法
由KGC 运行,输入params和s以及用户的身份ID,输出该用户的部分密钥DID,并通过安全信道返回给用户ID。
(3)用户秘密值生成算法
由用户运行,输入params和用户的身份ID,输出该用户的秘密值xID。
(4)用户私钥生成算法
由用户运行,输入params、用户的身份ID、部分密钥DID以及秘密值xID,输出该用户的私钥SKID。
(5)用户公钥生成算法
由用户运行,输入params、用户的身份ID、部分密钥DID以及秘密值xID,输出该用户的公钥PKID;
(6)签名算法
由签名者IDs运行,输入params、签名者的身份IDs、私钥公钥PKsID以及待签消息m,输出用户IDs对消息m的签名值。
(7)验证算法
由验签者IDv运行,输入params、签名者的身份IDs、公钥以及消息m和对应的签名值,若签名验证通过,输出“1若,表示接受,否则输出“0 表,表示拒绝。
1.3 无证书签名方案的攻击模型
无证书签名方案的攻击模型[15],通常被划分为两类:
A-I类:该类攻击者无法获取系统主密钥,但可以任意替换合法用户的公钥,也称为替换公钥攻击;
A-II类:该类攻击者可以获取系统主密钥,但不可以替换合法用户的公钥,也称为恶意不诚实KGC攻击。
无证书签名方案的不可伪造性的定义详见文献[15],本文在此不再赘述。
2 文献[14]签名方案回顾
(1)系统参数建立算法
输入安全参数k,输出2个大素数p、q,满足设P选择系统主密钥计算系统公钥P0=sP,系统公开参数:秘密保存主密钥s。是循环群G的一个阶为q的生成元。选择两个安全Hash 函数:
(2)部分私钥生成算法
输入params和用户的身份KGC随机选取计算作为用户IDa的部分私钥,aR作为用户的部分公钥,KGC 将通过安全信道发送给用户IDa。
(3)用户秘密值生成算法
(4)用户私钥生成算法
(5)用户公钥生成算法
(6)签名算法
③根据表1的公式计算计算v,表1共给出8个有效的签名方案,消息M的签名为
验证算法:

表1 签名与验证表
3 文献[14]签名方案的密码学分析
假设恶意攻击者Eve 希望假冒用户对消息M进行签名,用户的公钥
3.1 签名方案1的攻击
通过分析该方案中的T'的计算等式
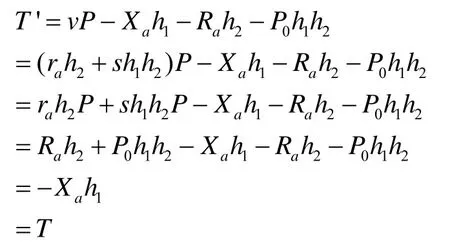
故有:
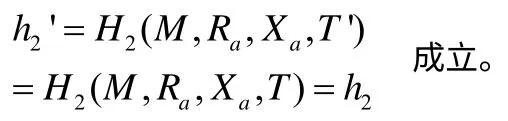
3.2 签名方案2的攻击
通过分析该方案中的T'的计算等式可知,对于不知道系统主密钥s的恶意攻击者Eve 而言,若想成功伪造签名值,只需借助替换后的公钥将带有随机因子T参与的摘要计算值2h的部分在运算中消除,从而可以通过T' 的计算等式计算出签名值中随机因子T,最终可以假冒用户aID构造出对任意消息M的有效签名值
恶意攻击者Eve 执行以下步骤即可成功假冒用户IDa伪造对任意消息M的签名:
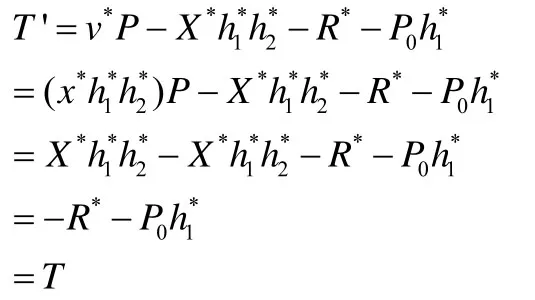
故有
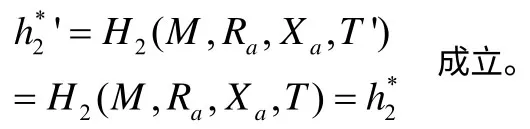
3.3 签名方案3的攻击
3.4 签名方案4的攻击
3.5 签名方案5的攻击
通过分析该方案中的T'的计算等式可知,该方案与方案2存在类似的安全漏洞,通过令恶意攻击者Eve 则可以假冒用户IDa构造出对任意消息M的有效签名值
3.6 签名方案6的攻击
通过分析该方案中的T'的计算等式可知,该方案与方案1存在类似的安全漏洞,通过令恶意不诚实的KGC则可以假冒用户IDa构造出对任意消息M的有效签名值
3.7 签名方案7的攻击
通过分析该方案中的T'的计算等式可知,恶意攻击者Eve 即使不替换用户IDa的公钥,也可以通过选择v的值,来构造对应的T,从而假冒用户IDa构造出对任意消息M的有效签名值(h2,v)。
恶意攻击者Eve 执行以下步骤即可成功假冒用户IDa伪造对任意消息M的签名:
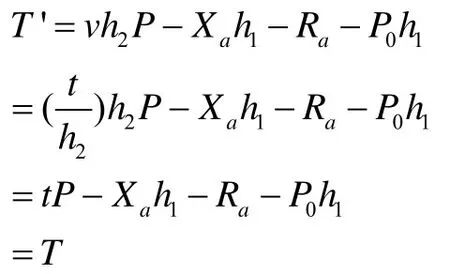
故有
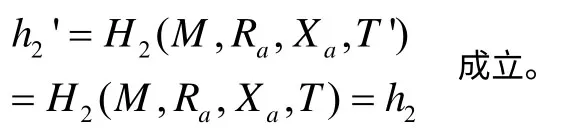
3.8 签名方案8的攻击
通过分析该方案中的T'的计算等式可知,该方案与方案7存在类似的安全漏洞,恶意攻击者Eve 即使不替换用户IDa的公钥,也可以通过选择v的值来构造对应的从而假冒用户IDa构造出对任意消息M的有效签名值
4 结束语
无证书签名在验证签名过程中无须直接验证签名者公钥的合法性,所以容易遭受恶意攻击者的替换公钥攻击;同时,因为KGC 掌握用户的部分私钥和系统主密钥,所以,也面临恶意不诚实KGC的攻击。本文对文献[14]中的8个无证书签名方案进行密码学分析后,发现都存在安全漏洞,并给出了具体的攻击方案,分析结论表明此类无证书签名方案是不安全的。
