初中数学函数动点问题教学策略探究

江苏省南通市如皋市江安镇江安实验学校 高 飞

各种函数知识与多种几何图形构成的“动点问题”，既是初中数学知识学习的重点与难点，也是各地数学中考常考的压轴大题，这类问题综合性强，对学生的思维能力、空间理解能力、计算能力等要求较高，对此类问题的教学应加强数学思想方法的渗透，注重分析和解决问题的能力培养，才能提高学生解题能力。

一、函数动点问题类型分析

在初中函数动点问题中，分为单动点问题和双动点（多动点）问题，在函数动点问题中常见的问题类型主要包括以下几类：

一是与直线相关的动点问题。这类问题主要有：点在直线上移动、点在数轴上移动问题。如，人教版初中数学第13 章中的“最短路径问题”，就涉及点在直线上移动的问题，此类型是单动点问题，问题主要是求直线上的动点到两点之间的最小值问题。该类问题又细化为两个定点在直线或数轴一侧、两定点分别在直线或数轴各一侧，这类问题可通过构建三角形、四边形或是利用图形对称性来解题。

二是与角相关的函数动点问题。与角有关的函数动点问题一般为等角型问题，即在图形或坐标区域内以一个或两个动点为顶点形成的角度等于已知角度问题。此类问题的解决主要依据“同弧（等弧）所对应的圆周角”来构造三角形或平行四边形等来求解。

三是与三角形相关的函数动点问题。这类动点问题主要包括：与特殊图形有关的动点问题，与三角形的周长、面积相关的动点问题，与三角形相似有关的动点问题。解决此类问题可根据勾股定理或几何图形的相关定理、两点间距离公式来解决。

四是与四边形相关的函数动点问题。这类动点问题主要包括：四边形的周长、面积最值问题求解，解决此类问题的重点是构建正方形、长方形、平行四边形等特殊四边形。

二、函数动点问题解题方法

要有效解决函数动点问题，应深入分析问题的性质和特点，构建恰当的辅助图形，掌握基本的解题思路与方法，就能快速有效解题。

一是分析题型，明白所求，也就是要根据问题判断是单动点、双动点问题判断是求图形的周长还是面积问题；二是分清变量，问题转化。对问题的“不变量”“变量”进行分析，把复杂的问题转化成简单的问题来处理；三是构造图形，分类讨论，也就是要根据问题来构建恰当图形，并对问题进行分类讨论；四是正确计算，结果检验。对问题进行求解，并对计算结果进行检验。

（1）确定B 点坐标与b 的值；

（2）判断△ABC 的形状；

（3）动点M 从A 点开始向B 点移动，其速度是2 单位/秒，同时动点N 从B 点开始向C 点移动，其速度是1 单位/秒。当M 点到达B 点时，N 点将停止运动。在两动点运动t 秒后，△MBN 与△ABC 相似，求t 的值。

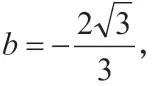
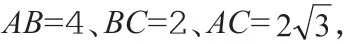
三、函数动点问题教学策略

一是克服畏难情绪。函数与几何图形相结合的动点问题是初中数学学习的难点，也是中考的压轴大题，许多学生对此存在畏难情绪，影响了解题能力的发挥，因此要帮助学生克服畏难情绪，调整心态，提高解题信心。

二是弄清运动过程。要看清题意，掌握几个运动的关键点，特别是起点、转折点、终点、运动速度，注重研究背景图形，根据题目合理构造几何图形来辅助解题，注重总结辅助线的添加方法与规律，能有效帮助解题。

三是渗透数学思想方法。解决函数动点问题经常要用到数形结合思想、转化思想、分类讨论思想等，掌握这些数学思想方法，有助于形成解题思路有效解题。

综上所述，要提高学生对函数动点问题的解题能力，需要教师加强数学思想方法的渗透教学，注重培养学生的数学思维能力与空间想象能力，重视总结动点问题的解题方法技巧，才能较好地提高学生解决此类难点问题的能力。