考虑换乘站点时间权重的公交时刻表优化
2020-03-06曹振宇
张 姚,曹振宇
考虑换乘站点时间权重的公交时刻表优化
张 姚,曹振宇
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 综合交通大数据应用技术国家工程实验室,成都 611756)
不同公交线路间的有效换乘是提高城市公共交通系统运行效率、减少乘客换乘等待时间的重要环节, 其核心是确定合理的公交发车时刻表。首先, 针对国内外公交时刻表优化设计现状进行分析, 提出不同出行目的乘客出行时间效用值不同的概念, 将其与换乘站点重要度结合考虑, 构建出了考虑换乘站点时间权重的最小化乘客换乘等待时间的优化设计模型, 并利用遗传算法对算例中的公交时刻表进行优化。与现有模型比较分析可知所建立的优化模型能减少公交网络总换乘等待时间,且换乘站点的时间权重越大, 该站点的换乘等待时间就越小, 与实际情况相符。
交通工程;换乘等待时间;公交时刻表优化;遗传算法;站点时间权重
0 引 言
公交线路时刻表设计问题是在一个特定的时间段内,决策单条线路的各车次到达或离开站点的时间,以权衡服务水平和运营成本。按照决策变量的类型,可以将时刻表优化设计分为两种形式:① 优化发车间隔时间或发车频率;② 优化车辆到站或离站时间。根据已有调查显示,公交出行乘客更加关注总的出行花费时间,而不是步行时间、换乘时间或车内乘车时间。随着城市规模的不断扩大,换乘必将成为乘客公交出行的一部分,考虑公交时刻表协同优化设计,即同时决策各线路车次从始发站的发车时间,使得不同线路的车辆协同到达换乘站点,减少乘客换乘等待时间[1]。
国内外针对公交时刻表设计与优化的研究相对较为成熟,但同时考虑站点效益值的研究还很少。2014年,Jens Parbo等[2]提出考虑乘客出行路径选择与换乘总等待时间最少的双层优化模型,并采用启发式算法进行模型优化求解。Rapp[3]以公交线网中换乘延误最小为目标、公交运营成本为约束条件,使用交互式绘图法确定发车时间间隔。W. Domschke[4]在发车频率已知的情况下提出一种发车时刻的二次可导数学模型,目标是在换乘站点同步到达时间,以便减少乘客的等待时间。Ceder[5]提出公交网络同步性最大化的时刻表制订,使同时到达网络连接点的公交车数量最大。2012年,Omar J.Ibarra- Rojas[6]提出考虑车辆协同到达时间窗的最大化车辆协同到站次数的公交时刻表协同模型,并采用GAMS/ CPLEX进行优化,求解效率得到改善。刘志刚 等[7]建立车辆调度和时刻表生成的双层规划模型以解决区域公交调度问题,上层模型为以最小化线路所需车辆数和总空驶时间为目标,下层模型以最小化乘客换乘时间为目标。陈石等[8, 9]提出建立以协调公交时刻表与单线原始时刻表偏差最小,区域换乘不满意度最小的多目标模型,从到站准点率、行程时间可靠度、服务间隔可靠度三方面调整公交发车时间间隔。田启华等[10]设置驻站时间松弛变量,以车辆在枢纽点相遇次数最大为目标函数,求解最佳发车时间和驻站时间。岳大振[11]以各时段发车间隔为决策变量,建立了基于乘客到站率的目标函数,为公交智能调度提供了思路。
总的说来,现有研究已开始关注以最小化乘客换乘等待时间为目标函数的公交网络时刻表协同优化设计问题,但由于设计优化问题涉及多个目标,且这些目标相互冲突,学者在建立模型的过程中考虑换乘站点重要程度的研究较少,未考虑乘客出行行为对公交时刻表的约束。在实际运行过程中,不同出行需求的乘客,对换乘时间的要求不同,往往需要重点考虑换乘需求较大的换乘站点。因此,本文提出不同出行目的乘客出行时间效用值不同的概念,将其与换乘站点重要度结合考虑,构建出了考虑换乘站点时间权重的最小化乘客换乘等待时间的优化设计模型,利用遗传算法对算例中的公交时刻表进行优化,并通过与已有研究结果对比分析验证该模型对时刻表优化的效果。
1 模型的建立
1.1 模型假设
考虑到公交车辆调度受多种外部因素的影响,在进行时刻表优化设计时需要针对研究问题进行相应简化,因此,本文做出如下假设:
① 公交车按照发车时间表准时发车,途中没有堵车及意外事故,即假设车辆在各路段的行驶时间是固定的;
② 为避免不同线路车辆在换乘站点发生串车现象,乘客换车的车辆与正乘坐车辆先后到达换乘站点的时间间隔应大于某一预先设定的值,并且乘客的换乘等待时间要小于预先设定的最大换乘等待时间;
③ 不考虑非换乘车站对行程时间的影响;
④ 假设不同时段发车间隔不同;
⑤ 运营车辆全部为全程车;
⑥ 乘客不会因为车辆拥挤而不上车,即不考虑车辆容量问题。
1.2 目标函数
以线路车次的发车时间作为决策变量,建立的公交发车时刻表设计优化模型,主要考虑换乘站点的效用值,以最小化加权换乘等待时间为目标函数,具体数学表达式如下:

(1)乘客协调换乘等待时间
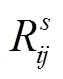

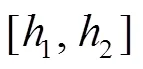







Tab.1 Beta values and share of trips
1.3 约束条件
本文主要考虑的约束条件为公交发车时间间隔约束、换乘等待时间协调性约束。
(1)公交发车时间间隔约束:考虑不均匀发车时间间隔的公交时刻表优化设计,为避免发车时间间隔变化太大,缺少一定规律,影响乘客出行,发车时间间隔存在最大发车间隔与最小发车间隔:





其中,为一个较大的正数;

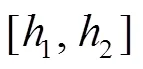
1.4 模型分析
已有相关文献提出固定发车间隔下的公交网络时刻表设计是一个NP-complete问题[12-14]。Ibarra-Rojas et al.[1]进一步解释了不固定发车时间间隔,以最大化车辆协同到达换乘站点的公交网络时刻表设计问题是一个NP-complete问题。在以上研究的基础上,本文考虑乘客出行目的和以最小化乘客换乘时间的时刻表优化问题为一个非线性非凸的混合整数优化问题,约束条件较多。对于这种复杂的非线性混合整数优化问题,不适合大规模遍历求解,传统优化算法较难得到该问题的精确结果,考虑使用现代寻优算法求解模型的局部最优解甚至全局最优解。目前的寻优求解算法主要有:遗传算法[15]、模拟退火算法[16]、蚁群算法[17]等。其中,遗传算法由于具有较强的全局搜索能力和鲁棒性被广泛应用,本文考虑采用遗传算法寻求近似最优解。
2 模型求解
步骤1 基于参考文献[14,18]中提到的针对发车时间可行解的空间特征,计算每个车次所有可行的发车时间、到站时间和协同时间窗。
步骤2 根据约束条件删除每队不可能协同达到的两车次对应的决策变量和约束,从而减少问题的求解空间。
步骤4 交叉操作。任选两个有换乘关系的个体,从两个个体中随机挑选线路进行交换,生成两个新的个体,为保证交叉变异后的个体是可行解,变异基因必须符合约束条件,即:

步骤5 变异操作。任选个体内的一条线路,改变线路的发车时间,为保证变异后的个体是可行解,变异基因必须符合约束条件。

3 算例设计及分析
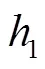

图1 算例的线路结构
采用遗传算法求解该模型,计算结果如表2所示。将本文的算例数据带入参考文献[6]和参考文献[14]的优化模型中,求解换乘等待时间。求解结果表明发车间隔时间在时间段[9, 11]范围内,最优解目标函数值为547 min,低于其他相关文献中求解出的最低值562 min,表明利用本文提出的模型和算法可以得到整个公交线网总的换乘时间最小的公交发车时刻表。从换乘时间相关性分析,本文考虑了每个换乘站影响系统总换乘等待时间的权重不同,即每个换乘站点的换乘等待时间的权重系数不同,本文中三个换乘站点权重系数分别为1.22、1.00、1.05,因此在进行时刻表协调优化时尽量减少换乘站点1的换乘等待时间,最大程度减少系统总的换乘等待时间。
表2 算例结果对比

Tab.2 Comparison results for models
图2为发车间隔在9 min到11 min区间波动时,历代解集所对应的最小目标函数值。由图2可知,遗传算法收敛速度较快,在第45代左右即达到相对较优解,最终目标函数值从1 600 min平稳下降至547 min。
调整发车时间间隔的最大值和最小值,改变线路的初始发车时刻,利用遗传算法求解不同发车间隔情况下的目标函数值,得到三种不同发车时间间隔情况下历代解集所对应的最小目标函数值。由图3可知,算法能较快收敛至统一解。

图2 算例收敛过程

从乘客总换乘等待时间这一指标分析该模型的有效性。从表2可以看出,与文献[6]相比,本文提出的模型科学合理的综合考虑了不同类型乘客出行时间权重,重点考虑重要换乘站点的换乘等待时间,有针对性地调整发车时间间隔,从而进一步减少了乘客总的换乘等待时间,以此验证了模型的有效性。
4 结 论
本文以总换乘等待时间最小化为目标,建立了综合考虑换乘站点时间重要程度的时刻表优化方法,以公交发车时间间隔、换乘等待时间协调性为约束条件,采用遗传算法对其进行优化求解,验证了模型的有效性。
(1)数值算例分析表明,换乘站点的时间权重越大,优化后该站点的换乘等待时间相对减少,这与实际协调重要换乘站点换乘的情况相符合。
(2)为了与已有研究相对比,本文以总换乘时间减少为衡量标准,验证模型的有效性。后续研究应通过数据采集获取线路实际运行数据,结合人工调查获取乘客实际等待时间,检验模型的时效性;现有模型是以确定的车辆行驶时间为基础进行设计的,这与实际车辆运行状况不符,进一步研究工作可以考虑车辆行驶时间不确定性下的时刻表优化问题。
[1] IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of bus timetabling[J]. Transportation Research Part B: Methodological, 2012, 46(5): 599-614.
[2] PARBO J, NIELSEN O A, PRATO C G. User perspectives in public transport timetable optimisation[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 269-284.
[3] RAPP M H. Man-machine interactive transit system planning[J]. Socio-Economic Planning Sciences, 1972, 6(1): 95-123.
[4] DOMSCHKE W. Schedule synchronization for public transit networks[J]. Operations-Research-Spektrum, 1989, 11(1): 17-24.
[5] CEDER A, GOLANY B, Tal O . Creating bus timetables with maximal synchronization[J]. Transportation Research, Part A: Policy and Practice, 2001, 35(10): 913-928.
[6] IBARRA-ROJAS O J, RIOS-SOLIS Y A. Synchronization of bus timetabling[J]. Transportation Research Part B: Methodological, 2012, 46(5): 599-614.
[7] 刘志刚, 申金升. 区域公交时刻表及车辆调度双层规划模型[J]. 系统工程理论与实践, 2007, 27(11): 135-141.
[8] 陈石. 区域公交时刻表生成的模型与方法研究[D]. 北京: 北京交通大学, 2009.
[9] 刘环宇. 基于可靠性的公交时刻表优化设计研究[D]. 北京: 北京交通大学, 2010.
[10] 田启华, 陈艳艳. 区域公交协调调度优化算法研究[J]. 交通运输系统工程与信息, 2011, 11(4): 160-165.
[11] 岳大振. 基于乘客到站率的公交发车时刻表优化研究[D]. 济南: 山东大学, 2014.
[12] ODIJK M A . A constraint generation algorithm for the construction of periodic railway timetables[J]. Transportation Research Part B: Methodological, 1996, 30(6): 0-464.
[13] 李东序. 优先发展城市公共交通是一项重要战略[J]. 城市交通, 2007, 5(1): 17-19.
[14] 吴影辉, 唐加福. 考虑不均匀发车间隔的公交网络时刻表优化模型[J]. 东北大学学报: 自然科学版, 2016, 37(4): 461-466.
[15] 孙红, 谭笑. 遗传算法在车辆调度优化问题中的研究[J]. 计算机工程与应用, 2010, 46(24): 246-248.
[16] 刘学智, 袁荣湘, 刘涤尘. 模拟退火算法在输电网络扩展规划中的应用[J]. 电力系统及其自动化学报, 2010, 22(2): 11-14.
[17] 郭茜, 聂润兔, 王超. 蚁群算法在解决空中交通飞行冲突中的应用[J]. 交通运输工程与信息学报, 2009, 7(2): 116-119.
[18] WU Y, TANG J, YU Y, et al. A stochastic optimization model for transit network timetable design to mitigate the randomness of traveling time by adding slack time[J]. Transportation Research Part C: Emerging Technologies, 2015, 52: 15-31.
Optimization Model for Public Transport Timetable with the Time Weight of Transfer Station
ZHANG Yao,CAO Zhen-yu
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China)
Effective transfer between different bus lines is an important aspect of improving the operation efficiency of urban public transport systems and reducing the waiting time for passenger transfer. To address these concerns, it is crucial that efficacious schemes should be implemented. In this respect, this study examines the status of domestic and international bus schedule optimization in detail. The concept of utility values for different travel times is then proposed for different travel purposes. This is considered in conjunction with the importance of the transfer station. An optimal design model for minimizing the passenger transfer waiting time by considering the utility value of the transfer station is constructed, and a genetic algorithm is developed in this study. Compared to existing models, the results show that the optimization model established in this report can reduce the total transfer waiting time of the public transport network. Moreover, the larger the time utility value of the transfer station, the smaller the transfer waiting time of the station, which is consistent with the actual situation.
traffic engineering; transfer waiting time; bus schedule optimization; genetic algorithm; time-weight transfer station
U491.51
A
10.3969/j.issn.1672-4747.2020.01.010
1672-4747(2020)01-0077-07
2019-03-10
重庆市交通运输工程重点实验室开放基金(2018TE04)
张姚(1995—),女,西南交通大学硕士研究生,研究方向:智能交通和城市公共交通,E-mail:1530496857@qq.com。
张姚,曹振宇. 考虑换乘站点时间权重的公交时刻表优化[J]. 交通运输工程与信息学报,2020,18(1):77-82, 98.
(责任编辑:刘娉婷)
