考虑多节点时间窗差异的集装箱多式联运路径选择研究

汤银英，戴炜东，陈 思

考虑多节点时间窗差异的集装箱多式联运路径选择研究

汤银英1,2，戴炜东1，陈 思1,2

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756）

基于多式联运网络, 考虑不同运输方式的能力以及工作时间窗和发车班期, 并且根据货主的具体货运需求, 构建了运输成本最小、运输时间最少的多目标0-1整数规划模型。通过决策运输路线、运输方式来优化运输路径, 采用非支配排序遗传算法 (NSGA-II) 以及二阶段编码的方式求解模型, 经过多次种群进化和非支配解筛选, 获得多式联运运输路线的Pareto非劣解集。最后以20个节点、39条运输弧、3种运输方式的多式联运网络为例进行算例分析, 验证了算法和模型的可行性和有效性。

多目标规划；路径选择；时间窗

0 引 言

集装箱多式联运具有高效便捷、安全可靠的优势，是降低物流成本、减少运输时间的有效方式，是货物运输发展的重要方向[1]。因此，集装箱多式联运路径规划一直国内外学者研究的主要方向，旨在提高多式联运的运输效率和服务质量[2]。

近年来，国内外学者对于集装箱多式联运路径优化问题进行了深入的研究。于雪峤等[3]在需求不确定性的基础上，考虑节点时间窗以及货主满意度，构建运输费用最小的路径优化模型。刘杰等[4]考虑出发时间对运输路径选择影响，将运输费用分为固定费用、路段运费、换装费以及等待花费，建立多式联运路径优化模型，采用改进的Dijkstra算法求解。张小龙等[5]在考虑运输时间窗的基础上，构建运输时间最短、运输费用最少、运输碳排放最小的多目标路径优化模型。魏宇[6]考虑节点能力以及节点时间窗，构建多商品流多式联运路径优化模型，最后采用Anylogic进行仿真求解。熊桂武[7]引入代理商的概念，构建多代理商、多运输方式的多式联运路径优化模型，采用遗传算法得出最优路径。刘杰等[8]考虑低碳环境下的多式联运问题，构建了碳排放最小，运输费用最低的多目标模型。雷定猷等[9]考虑长大货物的特性，以线路限界、线路承载能力、起重设备的起重能力为约束条件，构建了长大货物路径优化模型。申勇等[10]考虑危险废物的特性进行了路径规划。任刚等[11]将混合时间窗和班期引入路径选择模型。刘畅等[12]根据货物时间价值对货物进行路径规划。Sun等[13]考虑CO2的排放，以运输成本最低构建路径选择模型，最后利用LINGO进行求解。James等[14]以墨西哥为实例，在考虑运输时间与运输成本的基础上，采用Dijkstra算法得出了最优的路径。Mnif等[15]采用烟花算法求解多目标多式联运问题，并将其与CPLEX的求解结果进行对比分析，得出启发式算法效率更高的结论。

综上所述，本文作者在既有文献研究的基础上，考虑了如下方面的内容：

（1）时间窗。既有文献大多只是简单地给节点一个模式单一的时间窗，没有对不同运输方式的时间窗区别对待。例如公路运输较为自由，其时间窗为是一个时间段，而铁路和水运则有固定的班期，应为固定的时间点，因此给不同运输方式不同类型的时间窗。

（2）多货物品类。现有文献大多没有考虑节点运输方式能力，只是对单一货物进行路径优化研究，而现实生活中，节点能力不足会影响运输方案的实施。

（3）多目标。现有文献虽然构建了考虑运输时间和运输费用的多目标模型，但大多都是将其转化为单目标进行求解，没有求解Pareto解集。

因此，本文考虑不同节点不同运输方式的时间窗、能力、货物的运到时限、货主能接受的最大运输费用等因素，构建运输费用最小、运输时间最短的多目标模型，采用NSGA-II算法得到Pareto解集。

1 问题描述与建模

1.1 问题描述

集装箱多式联运选择过程中，多式联运人会考虑运输成本、运输时间等因素选择合适的路线将货物运输到目的地，运输路线会途经多个节点，进行多次换装。相邻节点间能通过公路、水运、铁路这三种方式来运输集装箱，不同运输方式的运输费用、运输速度、运输能力存在差异，并且在运输的过程中，节点有通过能力限制以及工作时间窗的限制。

1.2 符号说明

1.3 模型构建

考虑运输费用最小，运输时间最小的的多式联运路径选择模型可表示如下：

目标函数：

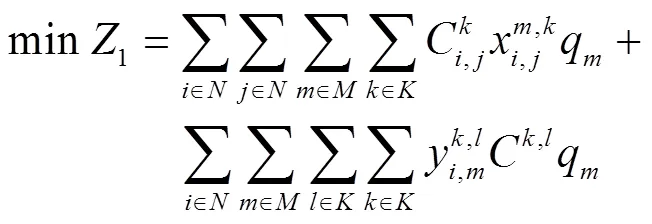
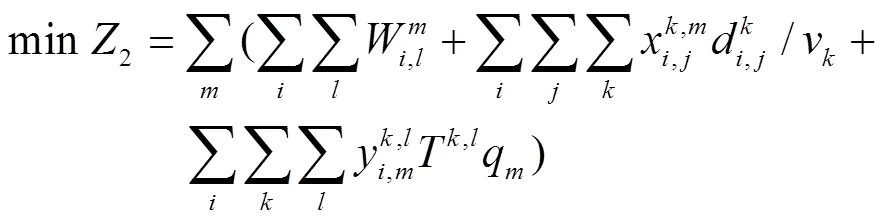
约束条件：

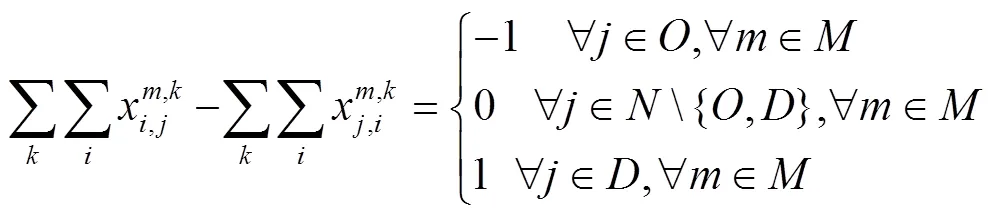
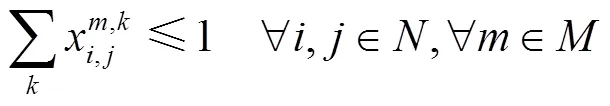
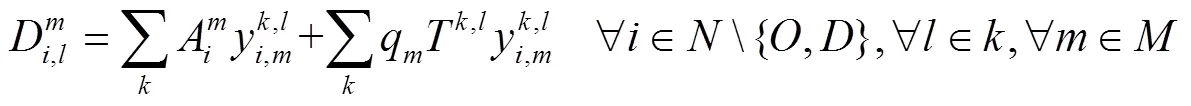
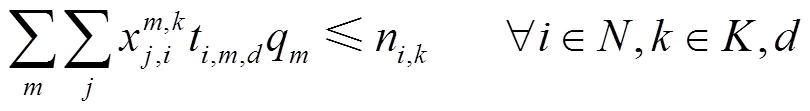
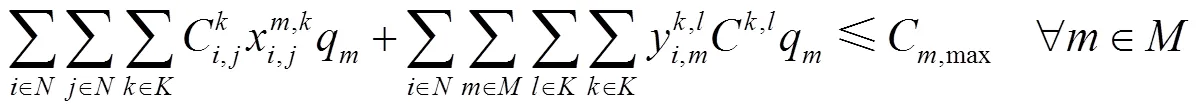
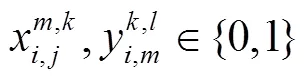
目标函数（1）表示总费用（运输费用、转运费用）最少；目标函数（2）表示总时间最少；约束（3）表示节点的流量平衡约束；约束（4）表示货物在两节点间运输最多只能选择一种运输方式；约束（5）为货物在节点至多转运一次；约束（6）为货物在节点转运时对运输路径的要求；约束（7）为货物到达节点的时间；约束（8）为货物在节点换装完的时间；约束（9）表示货物在节点用公路运输方式被运走需要等待的时间；约束（10）表示货物在节点用水运、铁路运输方式被运走需要等待的时间；约束（11）为货物离开起点的等待时间；约束（12）为货物到达节点的天数；约束（13）表示每一天到达节点的货运量要小于节点接收的能力；约束（14）为货物可接受的最长运输时间限制；约束（15）为货运需求可接收的最大运输费用限制；约束（16）为0-1变量，其中ceil（）函数为向上取整函数。

2 模型求解

上述问题是一个多目标问题，而针对多目标问题，适合采用多目标遗传算法NSGA-II进行求解。其基本原理对每个“染色体”的目标函数进行快速非支配排序，对每个“染色体”进行拥挤度计算，根据非支配关系以及拥挤度选取合适的“染色体”组成父代种群，在遗传算法的基础上产生新的子代种群，将父代染色体与子代染色体合并形成新的父代染色体，依此类推，得到Pareto解。具体计算过程如下：

（1）编码

在编码的时候，“染色体”分为两段，第一段为路径编码，采用优先级编码；第二段为运输方式编码，用1~3分别表示公路、铁路、水运三种运输方式，对图1进行编码，染色体如图2所示。

图1 运输网络图

图2 货运需求染色体

单货运路径部分6，2，1，4，3，5为节点的优先级，即节点1的优先级为6，节点2的优先级为2，以此类推。运输方式部分为线路运输方式编码。多货运需求与单货运需求的编码含义相同，不再赘述。

（2）解码

在对染色体进行解码，得到染色体表示的运输路线和运输方式，步骤如下所示：

step 1 先寻找每个节点的关联节点集。

step 2 将所有节点划分成两个集合、（包含起始节点，为其他节点）。

step 3 从集合末节点的关联节点集中选择优先级最大的节点，将归入集合，并且集合减去该节点。

step 4 当不等于终点时，重复第三步，直到为终点。

对图2（a）单货运需求染色进行解码（多货运需求类似），按照上述步骤进行解码后，路径为1—2—5—6，运输方式为2，2，1。

（3）适应值计算

通过解码得到的运输路径满足路径约束，但没考虑时间窗、运输能力、运输时限约束以及最大运输费用的约束。因此，对于时间窗约束，按照解码路径计算到达各节点的时间，如果到达时间在工作时间窗内，则按照路径去往下个节点，否则进行等待。对于节点能力约束，则根据货物到达节点的天数计算，用这一天的节点能力减去货物的数量，若得到的数小于零，则将运输时间和运输费用设为极大的数，反之，则不变。对于运输时限约束以及最大运输费用的约束，按照解码路径得到的运输时间和运输费用不满足约束时，则将运输时间和运输费用分别乘以惩罚系数1.5，反之，则不变。

（4）快速非支配排序

根据目标函数值，计算染色体的排序等级（rank）进行分层和选择，建立子代染色体种群。步骤为：

step 1 定义个体的适应度值若优于个体，则称支配，若没有被任何其他解支配，则称为非支配解。将所有非支配解的集合赋予rank = 1。

step 2 在除去非支配解外的剩余种群中再次找出非支配解集，赋rank = 2。

step 3 按照此原则进行，直到整个种群被分层，在分层的基础上计算染色体的拥挤度值，对相同排序等级的染色体按拥挤度进一步排序。

（5）选择

采用竞标选择算子，每次取两个染色体，比较排序等级，若排序等级值小，则该染色体进入子代种群，反之则被淘汰；若排序等级值相同则比较拥挤度，若拥挤度较大，该染色被淘汰，反之进入子代种群。

（6）交叉、变异

染色体交叉是随机选取两个染色体，分别将染色体的一段编码进行交换。染色体变异是随机变化染色体的编码，算法流程如图3所示。

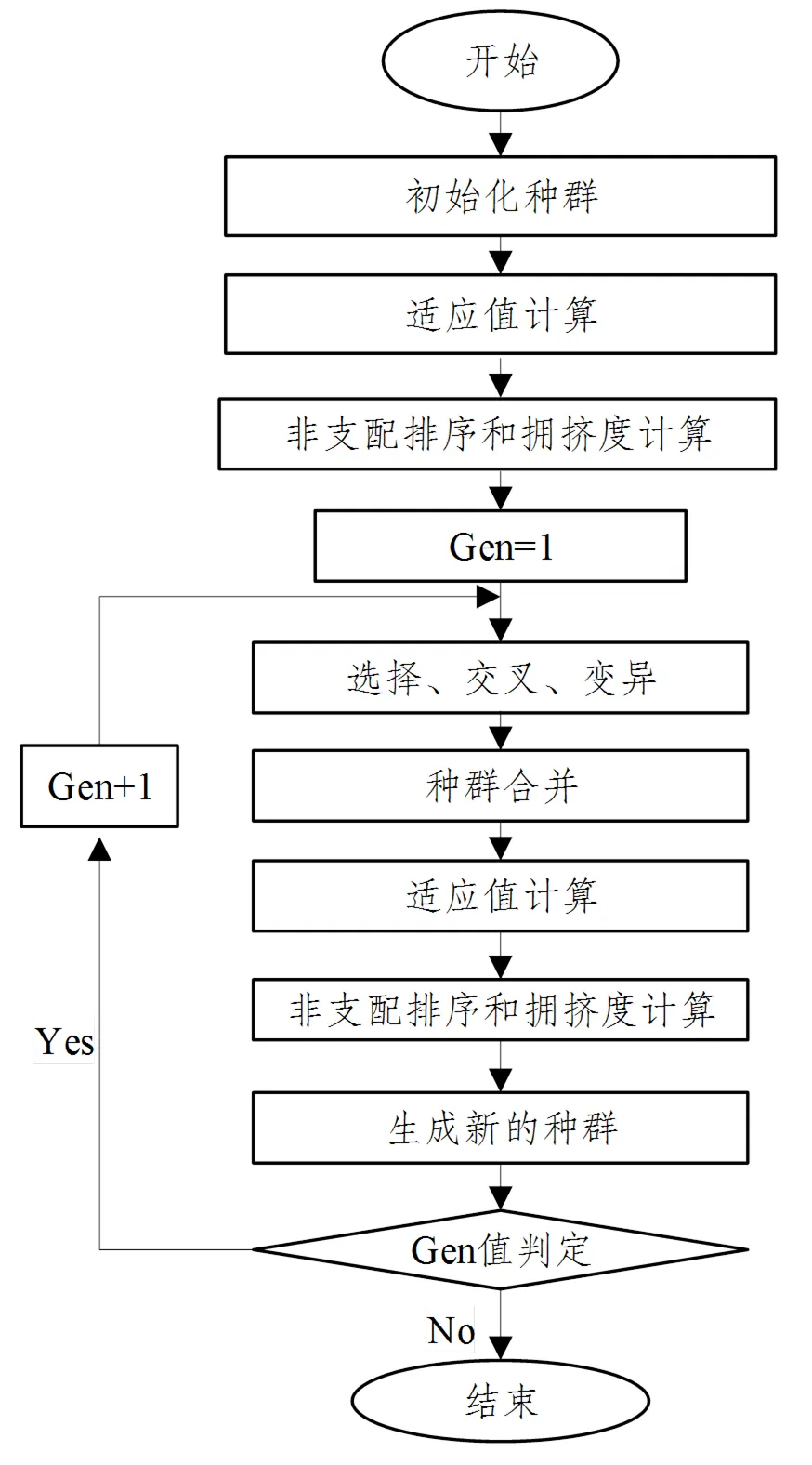
图3 算法流程图

3 算例分析

3.1 案例设计

为了考察模型和算法的可行性，模拟了具有20个节点的多式联运网络，运输弧段为39条，如图4所示。运输方式有3种，分别为铁路、公路、水运，设定公路的运输速度为60km/h，水运的速度为30km/h，铁路的速度为50km/h。

在网络中，运输网络均采用集装箱运输，各运输弧段不同运输方式的运输距离以及运输费用如表1所示。

表1 运输弧段的运输距离以及运输费用

多式联运网络中，节点运输方式能力限制以及时间窗如表2所示。

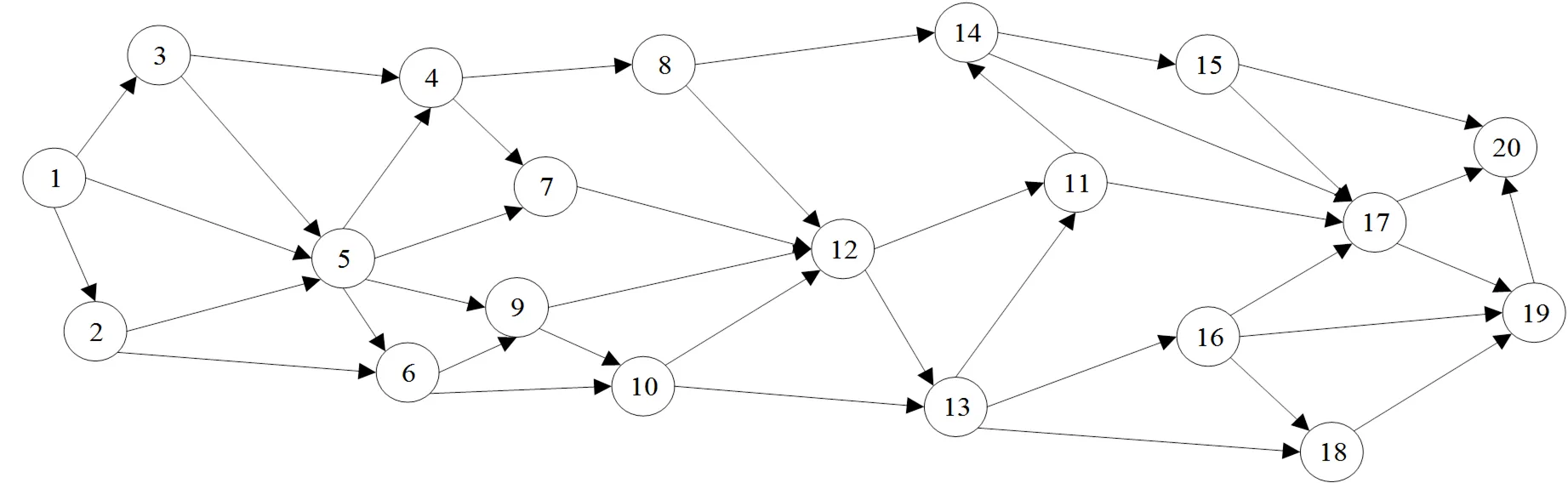
图4 多式联运网络

表2 节点的通过能力以及时间窗

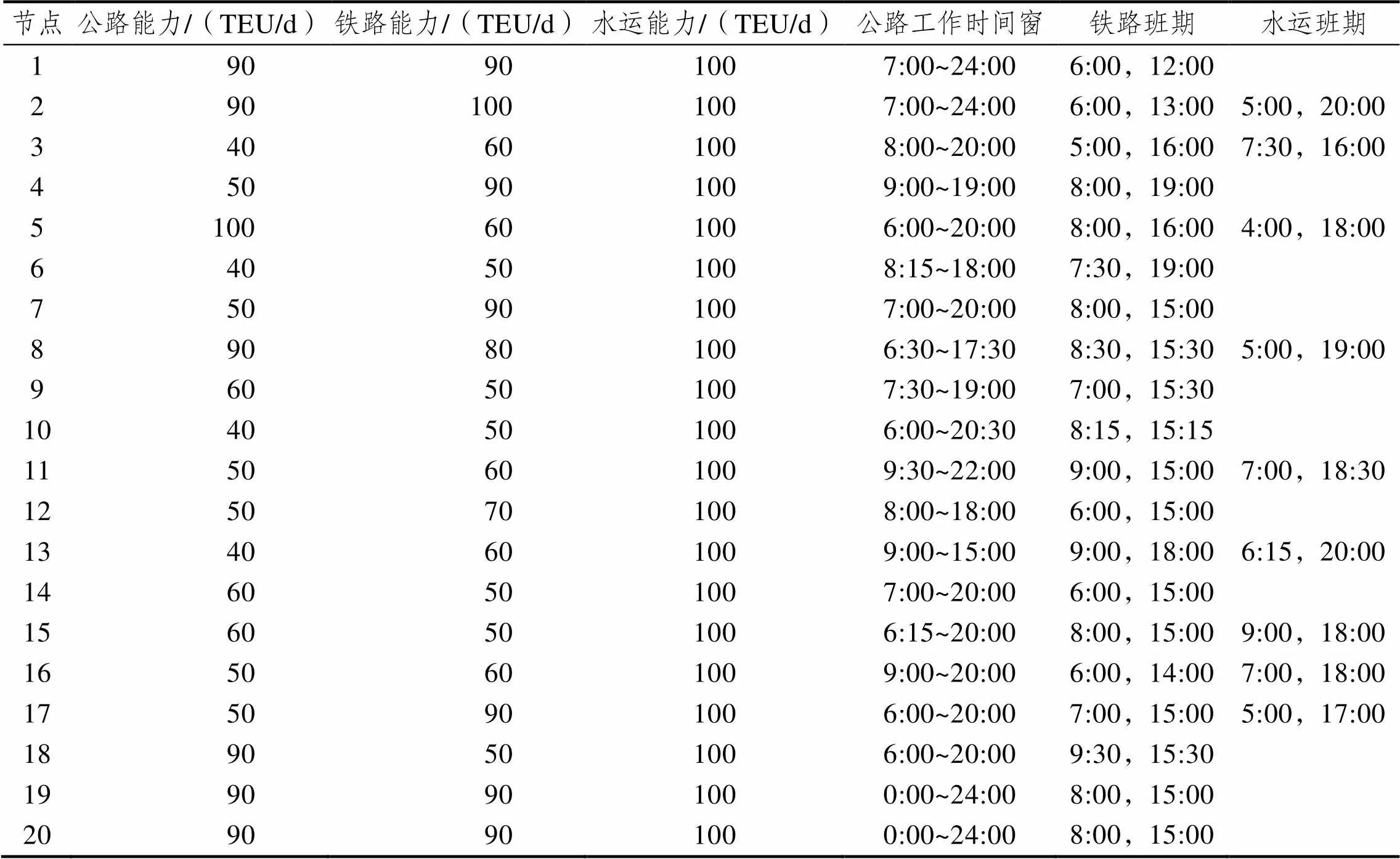
Tab.2 Node passability and time window

在多式联运网络中，运输方式转运时间、转运费用如表3所示，客户具体货物运输需求如表4所示。

表3 换装费用以及换装时间

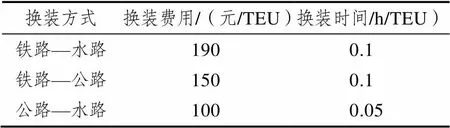
Tab.3 Transshipping cost and time

表4 货物运输需求

Tab.4 Cargo transportation demand

3.2 求解结果

运用matlab2016进行计算，设置变异概率为0.4，交叉概率为0.9，初始种群大小为100，最大进化次数为800次，计算时间为350s，得到Pareto最优解集，目标函数Pareto非劣解集的平均值如图5所示。

采用NSGA-II算法进行计算后，得到3个解，具体如表5所示。解集满足了客户对于运输费用和运输时间的要求。

在其他条件不变的基础上，改变客户的运输需求，需求1的运输时限为180h，最大可接受费用为360 000元，需求2的运输时限和最大可接受费用分别为105h和600 000元，如表6所示。

迭代次数

表5 Pareto解集

Tab.5 Pareto solution set

表6 货物运输需求

Tab.6 Cargo transportation demand

运用NSGA-II算法求解结果如表7所示。

表7 Pareto解集

Tab.7 Pareto solution set

比较表5和表7，可以看出当运输需求的最大可接受时间和最大可接受费用发生变化时，运输方案会发生变化。在现实运输过程中，在制定运输方案时，要具体考虑客户的运输需求。当运输需求的最大可接受费用较大，运输时限较小时，路径选择的过程中，会选择运输速度较快和运费较高的公路进行运输，反之，会选择铁路或者水运。

4 结 论

（1）考虑节点不同运输方式的能力、不同运输方式的运输时间窗以及客户的具体需求，构建了运输成本最小、运输时间最少的多目标0-1整数规划模型，采用NSGA-II算法进行求解，通过算例证明模型和算法的可行性和有效性。

（2）通过设定不同的运输需求，对不同的运输方案进行分析，当运输时限较小且客户可接受的费用较大时，运输方式主要选择公路。当运输时限较大且客户可接受的费用较小时，运输方式主要选择水运和铁路。当处于其他情况时，会采用公铁水这三种方式联运。

本文仍存在很多进一步研究的空间，例如考虑多式联运不同箱型的情况以及运输需求的不确定等因素，希望以后的研究在这些方面进一步完善。

[1] 胡元, 帅宇红. 整车物流运输多式联运与路径优化研究[J]. 交通运输工程与信息学报, 2019, 17(1): 13-18.

[2] 刘清, 朱新建, 周张颖, 等. 长江干线集装箱多式联运路径优化模型研究[J]. 武汉理工大学学报: 交通科学与工程版, 2019, 43(4): 622-626.

[3] 于雪峤, 郎茂祥, 王伟哲, 等. 考虑模糊需求的多式联运路径优化[J]. 北京交通大学报, 2018, 42(3): 23-29, 36.

[4] 刘杰, 何世伟, 宋瑞, 等. 基于运输方式备选集的多式联运动态路径优化研究[J]. 铁道学报, 2011, 33(10): 1-6.

[5] 张小龙, 陈小鸿. 混合时间窗约束下多目标多式联运路径优化研究[J]. 综合运输, 2018, 40(8): 98-104.

[6] 魏宇. 多路径多式联运网络组合优化问题研究[D]. 西安: 长安大学, 2016.

[7] 熊桂武. 带时间窗的多式联运运输优化研究[D]. 重庆: 重庆大学, 2014.

[8] 刘杰, 彭其渊, 殷勇. 低碳背景下的多式联运路径规划[J]. 交通运输系统工程与信息, 2018, 18(6): 243-249.

[9] 雷定猷, 游伟, 张英贵, 等. 长大货物多式联运路径优化模型与算法[J]. 交通运输工程学报, 2014, 14(1): 75-83.

[10] 申勇, 王子兰, 吴友发. 危险废物处理设施选址-路径模型研究[J]. 交通运输工程与信息学报, 2019, 17(3): 85-90, 108.

[11] 任刚, 刘畅, 高智源, 等. 考虑多周期和混合时间窗的中欧电子产品多式联运路径选择优化[J]. 系统工程, 2019, 37(6): 67-73.

[12] 刘畅, 关秀婷, 张金伟, 等. 考虑时间价值成本的中欧笔记本电脑多式联运路径优化研究[J]. 铁道科学与工程学报, 2019, 16(9): 2352-2359.

[13] SUN Y, LANG M. Modeling the multicommodity multimodal routing problem with schedulebased services and carbon dioxide emission costs[J]. Mathematical Problems in Engineering, 2015, 2015(4): 1-21.

[14] JAMES H B, NEIL S F. Intermodal routing of Canada–Mexico shipments under NAFTA[J]. Transportation Research Part E: Logistics and Transportation Review, 1998, 34(4): 289-303

[15] MNIF M, SADOK B. Firework algorithm for multi- objective optimization of a multimodal transportation network problem[J]. Procedia Computer Science. 2017, 112: 1670-1682.

Container Multimodal Transport Route Planning Considering the Difference in a Multi-node Time Window

TANG Yin-ying1, 2，DAI Wei-dong1，CHEN Si1, 2

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China)

Based on a multimodal transport network, a multi-objective 0-1 integer programming model with the lowest transportation cost and the smallest transportation time is constructed considering the capacity of different modes of transport, the working time window, the departure schedule, and the client’s specific cargo demand. Transportation routes are optimized by determining transportation routes and modes. The non-dominated sorting genetic algorithm II (NSGA-II) and the two-stage coding method are used to solve the model. After multiple population evolution and non-dominated solution screening, the Pareto non-inferior solution set of multimodal transport route is obtained. Finally, a multimodal transport network with 20 nodes, 39 transport arcs, and 3 modes of transport is taken as an example to analyze the feasibility and effectiveness of the algorithm and model.

multi-objective planning; path selection; time window

U169.62；F511.4

A

10.3969/j.issn.1672-4747.2020.01.005

1672-4747（2020）01-0034-09

2019-04-08

中国铁路总公司科技研究开发计划重点课题（2018BX15）；教育部人文社会科学研究西部青年基金项目（16XJCZH001）；四川省农村发展研究中心项目（CR1716）；西南交通大学双一流学科建设项目（YX1300112601801-2532）；四川民族山地经济发展研究中心项目（SDJJ1812）

汤银英（1979—），女，汉族，河南人，博士，西南交通大学交通运输与物流学院副教授，主要从事运输组织优化研究，E-mail：yinyingtang@swjtu.edu.cn

汤银英，戴炜东，陈思. 考虑多节点时间窗差异的集装箱多式联运路径选择研究[J]. 交通运输工程与信息学报，2020，18（1）：34-42.

（责任编辑：李愈）