移动无线传感器网络中抑制病毒传播模型

吴三柱，李 鹏，吴三斌

(1.西安石油大学 计算机学院，西安 710065； 2.陕西师范大学 计算机科学学院，西安 710119；3.榆林职业技术学院 管理工程系，陕西 榆林 719100)

0 引言

随着互联网的快速发展，网络安全逐渐成为一个潜在的巨大问题,例如，计算机系统漏洞、蠕虫攻击、恶意代码攻击等,因此，网络安全问题日益受到重视[1-3]。

近年来，国内外许多学者致力于研究病毒在网络中的传播[4-15],根据病毒传播的状态和转换关系，分别提出SI(Susceptible-Infected)模型[9]、SIS(Susceptible-Infected-Susceptible)模型[10]、SIR(Susceptible-Infected-Removed)模型[11]、SIRS(Susceptible-Infected-Removed-Susceptible)模型[12]、SEIRS(Susceptible-Exposed-Infected-Removed-Susceptible)模型[13]等。文献[9-10]分别提出了SI模型和SIS模型，网络中都只有易感节点和感染节点，SI模型中易感节点被感染节点感染病毒后终身处于感染状态，而SIS模型中易感节点被感染节点感染病毒后可以治愈，治愈后可以再次恢复为易感节点;文献[11-12]分别研究了SIR模型和SIRS模型，这两种模型中的网络都具有三种状态的节点，即在SI模型和SIS模型的状态中增加免疫节点,而SIR模型和SIRS模型的最大区别也是被免疫的节点能否再次被感染;文献[13]研究了SEIRS模型，在SIRS模型的基础上增加潜伏期状态，即易感节点被感染后先进入潜伏状态。这些模型的研究大多基于静态网络，即网络拓扑结构图不随时间变化，而现实网络中节点是移动的且具有一定的生命周期。

因此，迫切需要研究移动无线传感器网络中的病毒传播模型。本文基于以上进展，提出了更加符合现实中病毒传播的SIRD(Susceptible-Infected-Recovered-Dead)模型，该模型既考虑了病毒节点在移动过程中具有移动和停留状态，又考虑了网络中节点因物理器件的损坏或电量的耗尽而不能再发挥作用。

1 网络模型

假设网络区域是一个球体表面(因为球体表面无边界，节点在每个周期内扫过的面积不变)，其半径为R1，则球体表面积A为：

A=4πR12

(1)

网络中共有N个节点，节点均匀分布在区域内，则平均密度ρ为：

ρ=N/A

(2)

网络中节点之间状态转换关系如图1，网络中共有4种状态节点，分别为易感节点(Susceptible, S)、感染节点(Infected, I)、免疫节点(Recovered, R)、死亡节点(Dead, D)，分别用S(t)、I(t)、R(t)、D(t)表示在任意t时刻4种节点在网络区域中的比例。为了维持网络的正常生命周期，新的节点持续加入，假设新加入的节点为易感节点，加入率为α。要使网络中存活节点数维持不变，则死亡率也为α，由此可得：

(3)

(4)

由式(3)和(4)可得，在任意时刻t都有：

S(t)+R(t)+I(t)=1

(5)

图1 节点之间状态转换关系Fig. 1 State transition relationships between nodes

为了更好地刻画网络区域中感染节点的移动行为，将运动的时间T划分为多个周期，每个周期由移动时间Tmove和停留时间Tstay(在停留期间感染节点不再感染通信范围内的节点)两部分组成，可以划分为Tnumber个周期，如图2所示。

图2 时间T由多个周期组成Fig. 2 Time T consists of multiple periods

按照上述定义，则有：

Tnumber=⎣T/(Tmove+Tstay)」

(6)

假设感染节点以随机方向模型[16]为移动方式，其通信半径为r，移动速度为V，则感染节点在时间T内移动总时间为Ttotal，扫过的面积为SArea。图3给出一个周期内节点扫过的面积示意图。

图3 一个周期内节点扫过的面积Fig. 3 Area swept by nodes in one period

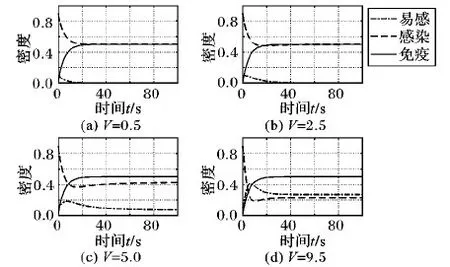
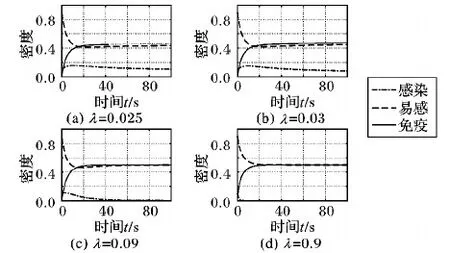
如果T-Tnumber(Tmove+Tstay)

Ttotal=T-TnumberTstay

(7)

如果T-Tnumber(Tmove+Tstay)≥Tmove，则：

Ttotal=Tmove+TnumberTmove

(8)

SArea=πr2Tnumber+2rVTtotal

(9)

一个感染节点在T时间内扫过的区域内有易感节点数CS(t)为：

CS(t)=SAreaρS(t)

(10)

然而，易感节点进入感染节点范围内并不意味着一定能够感染，事实上感染节点通过一定概率φ不断发送探测包来熟知通信范围内节点网络拓扑结构，一旦发现易感节点后，感染节点才发送病毒，进而以概率δ成功感染周边易感节点。假设此过程中感染节点发送探测包所耗费时间忽略不计,则感染节点成功感染易感节点概率σ为：

σ=φδ

(11)

则单位时间内，一个感染节点成功感染易感节点数NS(t)为：

NS(t)=σCS(t)/T

(12)

将式(11)、(10)、(9)、(2)、(1)代入式(12)得：

(13)

令β为：

(14)

则Ns(t)为：

Ns(t)=βS(t)

(15)

2 模型的建立与分析

2.1 模型的建立

根据图1所示节点之间状态转换关系，建立如下SIRD病毒传播动力学方程：

(16)

2.2 平衡点存在性分析

由式(5)可得在任意时间t总有R(t)=1-S(t)-I(t)，因此只需要求式(16)中S(t)和I(t)，即求下面二维系统模型:

(17)

(18)

(19)

因此，可以得到式(17)的基本再生数R0为：

(20)

定理1 当R0>1时，式(17)不仅有无病平衡解P0，还有地方病平衡解P1；当R0≤1时，式(17)只有无病平衡解P0。

证明 首先证明P0的存在性。

因为0<α<1,0<ε<1,所以S0=α/(α+ε)>0即P0(S0，I0)始终存在。

其次证明P1的存在性。

①当R0>1时，即：

②当R0<1时，即：

αβ/[(α+ε)(α+λ)]<1

③当R0=1时，即：αβ=(α+ε)(α+λ)，P1=P0，因此，式(17)只有唯一的解P1。

证毕。

2.3 系统稳定性分析

2.3.1 局部稳定性分析

为了探讨系统(17)在平衡点Px(Sx，Ix)处的稳定性，其中P0、P1∈Px，系统(17)在Px处的Jacobian矩阵为：

(21)

定理2 当R0≤1时，无病平衡解P0是局部渐进稳定的。

证明 将P0(α/(α+ε),0)代入式(21)得到P0处的Jacobian矩阵为：

(22)

J(P0)的特征多项式为：

a2Z2+a1Z+a0=0

(23)

当R0=1时，同样可得式(17)只有唯一的解P0。同上可得无病平衡解P0是局部渐进稳定的。

定理3 当R0>1时，地方病平衡解P1是局部渐进稳定的。

(24)

J(P0)的特征多项式为：

m2Z2+m1Z+m0=0

(25)

其中m0=αβ-(α+ε)(α+λ)，m1=αβ/(α+λ)，m2=1。

2.3.2 全局稳定性分析

定理4 当R0≤1时，无病平衡解P0是全局渐进稳定的。

证明 当R0≤1时，系统(17)只有无病平衡解P0。由李雅普诺夫(Lyapunov)稳定性理论[18]，构造函数Q(S，I)=I，由于在时间趋于无穷大时，无病平衡保证了S≤S0=α/(α+ε)，则Q函数对时间的全导数为：

I(βα/(α+ε)-λ-α)=

I[αβ-(α+ε)(α+λ)]/(α+ε)=

(α+λ)I[αβ/[(α+ε)(α+λ)]-1]=

(α+λ)I(R0-1)≤0

则根据李雅普诺夫(Lyapunov)稳定性理论，无病平衡解P0是全局渐进稳定的，病毒最终消亡。

定理5 当R0>1时，地方病平衡解P1是全局渐进稳定的。

证明 当R0>1时，确保了地方病平衡解P1的存在性。构造Dulac函数W(S，I)=1/I，令

M=α-βSI-εS-αS

N=βSI-λI-αI

则：

WM=α/I-(ε/I+α/I+β)S

WN=βS-λ-α

则根据Dulac判定定理可知，系统(17)在第一象限无闭轨线，故地方病平衡点P1是全局渐进稳定的，病毒将持续存在。

综上所述，由定理2～5可知：当R0≤1时，无病平衡解P0是全局渐进稳定的；当R0>1时，地方病平衡解P1是全局渐进稳定的。在病毒传播中物理意义：1)当控制基本再生数R0≤1时，随着时间的推移，在某一刻，网络中的感染节点消亡，即I0=0，易感节点和免疫节点的密度分别为S0、1-S0。此时，网络中存活的节点只有易感节点和免疫节点且密度维持不变，从而有效地将网络中的病毒全部查杀；2)当控制基本再生数R0>1时，随着时间的推移，在某一刻，网络中的感染节点、易感节点和免疫节点的密度分别变为恒定值I0、S0、1-I0-S0。此时，网络中存活的感染节点、易感节点和免疫节点密度维持不变，从而有效地控制病毒在网络中扩散。

3 实验评估

由上面理论可知：当R0≤1时，无病平衡解P0是全局渐进稳定的，即系统存在无病平衡解且该解是全局稳定的，病毒最终消亡；当R0>1时，地方病平衡解P1是全局渐进稳定的，即系统存在地方病平衡解且该解是全局稳定的，病毒将持续传播并稳定在一定的比例。为了验证所得结论的正确性和一致性，本文采用实验验证，通过分析各参数与R0关系，进而得出结论。仿真环境使用Matlab软件，利用控制变量法来实现。在求解过程中，时间复杂度O(f(n))中的f(n)与仿真总时长成正比，故其时间复杂度为O(n)。实验用到参数设置如表1所示。

表1 仿真参数设置Tab. 1 Simulation parameter setting

3.1 通信半径r对传播的影响

由式(14)和(20)可得：

(26)

令R0≤1且将各参数代入式(26)得：

9πr2+10 800r-50 000π≤0

-396.188 1≤r≤14.022 5

故R0≤1，即01，即r>14.022 5。分别取r=5、10、20、30，可得时间与节点密度变化曲线，如图4和图5所示。

当r=5、10时，即R0<1，无病平衡解分别为P0(0.5，0)和P0(0.5，0)是全局稳定的，感染节点最终消亡。从图4和图5的(a)和(b)可知，r=5、10时，随着时间的推移，感染节点的密度趋于0，易感节点和免疫节点的密度趋于相等的恒定值，即网络中的病毒全部查杀完毕，网络趋于全局稳定状态。

当r=20、30时，即R0>1，地方病平衡解分别为P1(0.345 4，0.154 6)和P1(0.224 7，0.275 3)是全局稳定的，感染节点将持续感染易感节点并稳定在一定的比例。从图4和图5(c)、(d)可知，r=20、30时，随着时间的推移，感染节点、易感节点和免疫节点的密度分别趋于恒定值，即网络中的病毒得到有效控制，防止了病毒扩大传播。

图4 不同r下I(t)随时间t变化曲线Fig. 4 I(t) changing with time t under different r

图5 不同r下S(t)，I(t)，R(t)随时间t变化曲线Fig. 5 S(t), I(t) and R(t) changing with time t under different r

3.2 移动速度V对传播的影响

令R0≤1且将各参数代入式(26)得：V≤4.283，所以R0≤1，即01，即V>4.283。分别取V=0.5、2.5、5.0、9.5，可得时间与节点密度变化曲线，如图6和图7所示。

图6 不同V下I(t)随时间t变化曲线Fig. 6 I(t) changing with time t under different V

当V=0.5、2.5时，即R0<1，无病平衡解分别为P0(0.5，0)和P0(0.5，0)是全局稳定的，感染节点最终消亡。从图6和图7的(a)和(b)可知，V=0.5、2.5时，随着时间的推移，感染节点的密度趋于0，易感节点和免疫节点的密度趋于相等的恒定值，即网络中的病毒全部查杀完毕，网络趋于全局稳定状态。

当V=5.0、9.5时，即R0>1，地方病平衡解分别为P1(0.429 4，0.070 6)和P1(0.227 7，0.272 3)是全局稳定的，感染节点将持续感染易感节点并稳定在一定的比例。从图6和图7的(c)和(d)可知，V=5.0、9.5时，随着时间的推移，感染节点、易感节点和免疫节点的密度分别趋于恒定值，即网络中的病毒得到有效控制，防止了病毒扩大传播。

图7 不同V下S(t)，I(t)，R(t)随时间t变化曲线Fig. 7 S(t), I(t) and R(t) changing with time t under different V

3.3 节点密度ρ对传播的影响

由式(14)和式(20)可得：

(27)

令R0≤1且将各参数代入式(27)得：ρ≤0.011 28，所以R0≤1，即0<ρ≤0.011 28；R0>1，即ρ>0.011 28。分别取ρ=0.005、0.010、0.020、0.030，可得时间与节点密度变化曲线，如图8和图9所示。

图8 不同ρ下I(t)随时间t变化曲线Fig. 8 I(t) changing with time t under different ρ

图9 不同ρ下S(t)，I(t)，R(t)随时间t变化曲线Fig. 9 S(t), I(t) and R(t) changing with time t under different ρ

当ρ=0.005、0.01时，即R0<1，无病平衡解分别为P0(0.5，0)和P0(0.5，0)是全局稳定的，感染节点最终消亡。从图8和图9的(a)和(b)可知，ρ=0.005、0.01时，随着时间的推移，感染节点的密度趋于0，易感节点和免疫节点的密度趋于相等的恒定值，即网络中的病毒全部查杀完毕，网络趋于全局稳定状态。

当ρ=0.02、0.03时，即R0>1，地方病平衡解分别为P1(0.282，0.218)和P1(0.188，0.312)是全局稳定的，感染节点将持续感染易感节点并稳定在一定的比例。从图8和图9的(c)和(d)可知，ρ=0.02、0.03时，随着时间的推移，感染节点、易感节点和免疫节点的密度分别趋于恒定值，即网络中的病毒得到有效控制，防止了病毒扩大传播。

3.4 易感节点免疫率ε对传播的影响

令R0≤1且将各参数代入式(26)得：ε≥0.041 2，所以R0≤1，即ε≥0.041 2；R0>1，即ε<0.041 2。分别取ε=0.02、0.03、0.09、0.9，可得时间与节点密度变化曲线，如图10和图11所示。

图10 不同ε下I(t)随时间t变化曲线Fig. 10 I(t) changing with time t under different ε

图11 不同ε下S(t)，I(t)，R(t)随时间t变化曲线Fig. 11 S(t), I(t) and R(t) changing with time t under different ε

当ε=0.09、0.9时，即R0<1，无病平衡解分别为P0(0.526 3，0)和P0(0.1，0)是全局稳定的，感染节点最终消亡。从图10和图11的(c)和(d)可知，ε=0.09、0.9时，随着时间的推移，感染节点、易感节点和免疫节点的密度分别趋于恒定值，即网络中的病毒得到有效控制，防止了病毒扩大传播。

当ε=0.02、0.03时，即R0>1，地方病平衡解分别为P1(0.708 2，0.075 1)和P1(0.708 2，0.039 7)是全局稳定的，感染节点将持续感染易感节点并稳定在一定的比例。从图10和图11的(a)和(b)可知，ε=0.02、0.03时，随着时间的推移，感染节点的密度趋于0，易感节点和免疫节点的密度趋于相等的恒定值，即网络中的病毒全部查杀完毕，网络趋于全局稳定状态。

3.5 感染节点病毒查杀率λ对传播的影响

令R0≤1且将各参数代入式(26)得：λ≥0.041 2，所以R0≤1，即λ≥0.041 2；R0>1，即λ<0.041 2。分别取λ=0.025、0.03、0.09、0.9，可得时间与节点密度变化曲线，如图12和图13所示。

图12 不同λ下I(t)随时间t变化曲线Fig. 12 I(t) changing with time t under different λ

图13 不同λ下S(t)，I(t)，R(t)随时间t变化曲线Fig. 13 S(t), I(t) and R(t) changing with time t under different λ

当λ=0.09、0.9时，即R0<1，无病平衡解分别为P0(0.5，0)和P0(0.5，0)是全局稳定的，感染节点最终消亡。从图12和图13的(c)和(d)可知，λ=0.09、0.9时，随着时间的推移，感染节点、易感节点和免疫节点的密度分别趋于恒定值，即网络中的病毒得到有效控制，防止了病毒扩大传播。

当λ=0.025、0.03时，即R0>1，地方病平衡解分别为P1(0.442 6，0.091 8)和P1(0.460 3，0.061)是全局稳定的，感染节点将持续感染易感节点并稳定在一定的比例。从图12和图13的(a)和(b)可知，λ=0.025、0.03时，随着时间的推移，感染节点的密度趋于0，易感节点和免疫节点的密度趋于相等的恒定值，即网络中的病毒全部查杀完毕，网络趋于全局稳定状态。

3.6 加入比例(死亡率)α对传播的影响

令R0≤1且将各参数代入式(26)得：

2 500πα2+(482π-2 160)α+25π≥0

上面等式恒成立，故0<α<1，所以R0≤1，即0<α<1；R0>1，无解。分别取α=0.1、0.3、0.6、0.9，可得时间与节点密度变化曲线，如图14和图15所示。

当α=0.1、0.3、0.6、0.9时，即R0<1，无病平衡解分别为P0(0.5,0)、P0(0.75,0)、P0(0.8571,0)、P0(0.9,0)是全局稳定的，感染节点最终消亡。从图14和图15可知，α=0.1、0.3、0.6、0.9时，随着时间的推移，感染节点的密度都趋于0，易感节点和免疫节点的密度分别趋于恒定值，α值越大感染节点趋于0用时越短，即α的值只要在取值范围内且其取值越大病毒被查杀的速度越快，网络中的病毒最终全部查杀完毕，网络趋于全局稳定状态。

图14 不同α下I(t)随时间t变化曲线Fig. 14 I(t) changing with time t under different α

图15 不同α下S(t)，I(t)，R(t)随时间t变化曲线Fig. 15 S(t), I(t) and R(t) changing with time t under different α

当α=0时，无病平衡解为P0(0，0)是全局稳定的，感染节点和易感节点最终消亡，即此时变为SIR模型，如图16。

图16 α=0时S(t)，I(t)，R(t) 随时间t变化曲线Fig. 16 S(t), I(t) and R(t) changing with time t at α=0

以上通过对节点通信半径、移动速度、密度、易感节点免疫率、感染节点病毒查杀率和节点死亡率等6个参数讨论及仿真实验。综上可得仿真结果与理论一致，因此本文模型可以很好地对仿真参数控制，进而达到预期效果。

4 结语

针对移动无线传感器网络中现有的病毒传播模型，本文提出了更加符合现实中病毒传播的SIRD模型。之后基于该模型建立了微分方程组，分析了平衡点存在性和系统稳定性，得出结论，当R0≤1时，系统存在无病平衡解且该解是全局稳定的，病毒最终消亡；当R0>1时，系统存在地方病平衡解且该解是全局稳定的，病毒将持续传播并稳定在一定的比例。最后基于R0讨论了节点通信半径、移动速度、密度、易感节点免疫率、感染节点病毒查杀率和节点死亡率对移动无线传感器网络中病毒传播的影响，并通过仿真实验验证了该模型的正确性和一致性。