考虑肥料溶解的压差施肥罐出口肥液浓度计算方法
2020-03-05胡昕宇严海军
胡昕宇,严海军,陈 鑫
考虑肥料溶解的压差施肥罐出口肥液浓度计算方法
胡昕宇,严海军,陈 鑫※
(1. 中国农业大学水利与土木工程学院,北京 100083;2. 中国农业大学北京市供水管网系统安全与节能工程技术研究中心,北京 100083)
压差施肥罐在中国的水肥一体化中得到了十分广泛的应用。该研究基于含源项的肥料输移扩散连续方程推导了考虑肥料溶解的压差施肥罐出口肥液浓度变化的理论公式,并通过参数描述肥料溶解过程对压差施肥罐出口肥液浓度变化的影响。通过与试验数据对比,理论公式计算的无量纲出口肥液浓度平均绝对偏差、均方差、几何平均偏差、几何方差和两倍偏差之间的预测分数的平均值分别为0.04、0.06、0.89、1.19和88.26%,验证了理论公式对出口肥液浓度计算的准确性。当参数取特定值时,理论公式可以转化为目前广泛应用的无量纲出口肥液浓度压差施肥罐出口肥液浓度的负指数公式。在此基础上,当罐内肥液浓度持续饱和且有充足的肥料可供长期溶解施肥时,考虑肥料溶解过程的均匀施肥方法被进一步探讨。该研究提出的考虑肥料溶解的压差施肥罐出口肥液浓度的计算方法可以实现压差施肥罐出口肥液浓度的准确预测,为考虑肥料溶解的均匀施肥提供可行方案。
肥料;溶解;水肥一体化;压差施肥罐;出口浓度;理论公式;均匀施肥
0 引 言
施肥作业对中国的粮食产量做出了巨大贡献[1],但肥料过量使用和低利用率对土壤、水环境和空气造成了不同程度的污染[2-3]。研究表明,降低肥料使用量和提高肥料利用率可以在不影响产量的前提下减轻对环境的破坏[4-5]。因此,优化现有施肥设备与施肥方法对中国的农业发展具有重要意义。压差施肥罐由于成本低、使用简便等优点,在中国微灌水肥一体化系统中应用十分广泛[6-9]。准确描述不同工作条件下压差施肥罐出口肥液浓度随时间的变化过程,可以为应用压差施肥罐的微灌系统的优化设计和运行、特别是以最优浓度实现均匀施肥提供合理建议。因此压差施肥罐出口浓度的计算方法值得进一步探究[10]。
目前,已有不少压差施肥罐出口肥液浓度随时间变化规律的研究。封俊等[11-12]假定水肥瞬间混合均匀且罐内肥液浓度均匀分布,结合试验数据较早提出了压差施肥罐出口肥液浓度负指数衰减的理论公式。孟一斌等[6,13]对不同施肥量和压差等条件下压差施肥罐出口肥液浓度的动态变化过程进行了测试分析,建立了估算压差施肥罐出口肥液浓度的回归模型。邓兰生等[14-20]通过试验分析了应用压差施肥罐进行施肥时压差、罐体体积、进出口管径、流量以及肥料品种、形态、用量等因素对出口肥液浓度衰减过程的影响。韩启彪等[21-22]应用计算流体动力学中的两相流模型及组分输运模型对压差施肥罐出口肥液浓度衰减过程进行了模拟研究,探讨了数值模拟方法预测压差施肥罐出口肥液浓度变化的可行性,并在肥料完全溶解且水肥瞬间混合均匀的前提下建立了基于压差施肥罐的均匀施肥方法。然而在实际施肥过程中,罐内通常会有大量肥料不断溶解,较大地影响以上研究的结论。基于以上工作,还需要考虑肥料溶解过程,提出压差施肥罐出口肥液浓度的计算方法服务于压差施肥罐的水肥一体化施肥作业。
本研究考虑肥料溶解过程的影响,借助含源项的肥料输移扩散连续方程并通过参数描述肥料溶解,推导压差施肥罐出口肥液浓度变化的理论公式。在此基础上,以最优浓度实现均匀施肥为目标,提出在特殊工况下考虑肥料溶解过程的均匀施肥方法,以用于指导压差施肥罐的施肥作业,为应用压差施肥罐的微灌系统的优化设计和运行提供参考。
1 考虑肥料溶解的出口肥液浓度理论公式
在压差施肥罐施肥过程中,肥料输运可以通过含源项的物质输移扩散连续方程进行描述[23],如式(1)。
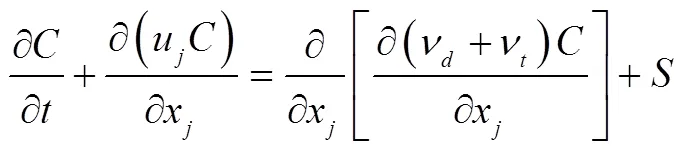
式中为罐内任一点的肥液浓度,%;为施肥时间,s;x(=1,2,3)为笛卡尔坐标系中的3个方向;u为水流在x方向的速度,m/s;ν为肥料离散系数,m2/s;ν为紊动扩散系数,m2/s;代表肥料不断溶解在输移扩散方程中产生的源项,其量纲与溶解速度相同,1/s。对式(1)在罐体内积分并通过积分变换[22],施肥罐出口肥液浓度可表示为

式中0为出口肥液浓度,%;为压差施肥罐的进口流量,m3/s;0()=∫∫∫d,是式(1)中源项在罐体区域的体积分,m3/s;为压差施肥罐的体积,m3。式(2)的解是

如图1所示,水流进入压差施肥罐后会发生剧烈翻转和混合。参考Noyes-Whitney方程[24],同种肥料在水中的溶解速度与接触表面积和肥液浓度与饱和浓度的浓度差有关。在施肥过程中,随着水流流入,罐体底部的肥料不断溶解,肥料与水的接触表面积不断减小,肥液浓度与饱和浓度的浓度差也不断减小。因此t=0时S0最大,随着施肥进行S0会不断减小至忽略不计。
考虑到肥料与水的接触表面积和肥液浓度与饱和浓度的浓度差的衰减趋势,0随时间的变化关系可以简化为负指数形式[25-26]。为了使出口肥液浓度公式简洁,考虑Burt等[27]以有效施肥浓度为准则定义的压差施肥罐施肥时间=4/,本文定义0的表达式为

式中代表罐内肥料初始溶解的速度,0≤≤1;代表罐内肥料溶解速度下降的快慢,≥0。当≠1时,将式(4)代入式(3)得考虑肥料溶解的出口浓度理论公式为

当0(0)为肥料的饱和浓度时,若=1、=0,源项式(4)和出口肥液浓度式(5)均为常数,此时罐内肥液浓度持续饱和且有充足的肥料可供长期溶解施肥。
=1是式(5)的可去间断点。当=1时,将式(4)代入式(3);或对式(5)取=1极限,均得
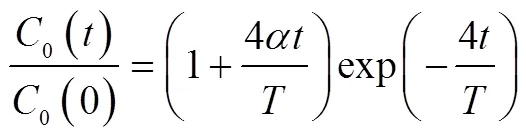
当=0或→∞时,0=0,此时罐内不存在肥料的溶解过程,式(5)退化为封俊等[11]提出的负指数衰减公式

式中C为负指数衰减公式的出口肥液浓度,%。这与封俊等的推导一致[11],此时肥料离散系数ν无穷大、罐内肥料与水流瞬间均匀混合且无肥料溶解。现有研究主要采用随时间呈负指数衰减的公式[6,10,13]逼近式(5),无肥料溶解时其指数值上限为4,即式(7);肥料的溶解使实际浓度大于式(7)的计算值,其指数值理论上小于4,如孟一斌等[6]和Li等[13]的拟合式
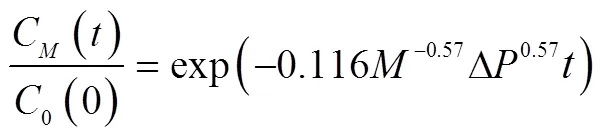
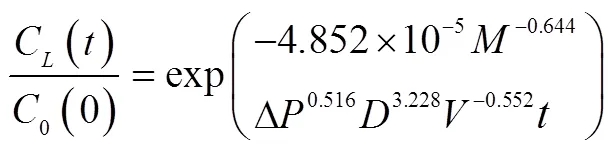
式中为压差施肥罐的施肥量,kg;Δ为压差施肥罐两侧的压差,MPa;为压差施肥罐的进出口管径,mm。式(8)的指数形式只考虑了施肥量和压差2个因素,而式(9)的指数与施肥量、压差、管径和罐体体积有关。然而式(8)~式(9)只考虑了各自研究中的施肥试验,并且均非基于量纲分析拟合而无法排除其他变量的影响,如压差和流量有关,罐体体积相同时直径、高度亦有所区别,不同罐体能量损耗系数差异对流量影响不同,使得前述拟合精度较低。可靠的做法是确定式(4)中描述肥料溶解过程的和。
2 理论公式验证与结果分析
2.1 α和β的变化对理论公式的影响
本节先分析和的变化对式(4)~式(6)的影响。基于式(4),图2对比了当和在各自取值范围内变化时(0≤≤1;≥0),无量纲源项(0()/(0(0)))随无量纲时间(/)的变化规律。图2a和2b分别为=0.5及=2.0时,不同对应的无量纲源项随时间的衰减趋势。在式(4)中表征罐内肥料的初始溶解速度,当取不同值时,0的初始值不同,大小为0(0)。考虑到式(4)的负指数形式,在取值不发生变化的前提下,随着的增大,相同时间内0的衰减也会随之增大。当=0时,罐内肥料的溶解速度为0(0≡0),说明此时不存在肥料的溶解过程。图2c和2d为=1.0时,不同对应的无量纲源项随时间的变化。在式(4)中代表罐内肥料溶解速度下降的快慢,当保持不变时,随着的增大,0的衰减速度从0增大至∞,0衰减至0所需的时间也不断缩短。当=0时,0恒等于0(0),此时肥料的溶解速度保持恒定,罐内肥液浓度持续饱和;当→∞时,0恒等于0,说明罐内不存在肥料的溶解。

注:Q为进口流量,m3·s-1;C0(0)为出口初始肥液浓度,%;S0(t)为某时刻t源项S在罐体区域的体积分,m3·s-1;α代表罐内肥料初始溶解的速度;β代表罐内肥料溶解速度下降的快慢。下同。
基于式(5)~式(6),图3对比了不同和取值无量纲化的出口肥液浓度(0()/0(0))随无量纲时间(/)的变化过程。由于式(5)~式(6)是式(4)代入到式(3)中求解得到,因此,图3中0的变化与图2中0的变化过程对应。图3a和3b中在取值不发生变化时,随着的增大,0的衰减趋势逐渐变缓,尤其是施肥初始阶段0的变化曲线明显平缓。这是由于的增大导致0的初始值增大(图2a~图2b),即更多的肥料溶解,因此导致的0衰减速度变缓。图3c和3d中当=1.0时,0的衰减趋势随着的增大而逐渐明显并且不断逼近式(7)(→∞)。但相同的增量对0变化幅度的影响却在逐渐减小。这是由于随着的增大,肥料溶解速度的变化率从0增大到∞,0的衰减速度从0变化至∞(图2c~图2d),即肥料溶解过程对出口肥液浓度变化的影响越来越小。当=0时,0≡0(0),此时肥料的溶解速度保持恒定,罐内肥液浓度恒为0(0);当→∞时,式(5)退化为负指数衰减的式(7),说明此时不存在肥料溶解。

注:C0(t)为某时刻t出口肥液浓度,%。
2.2 理论公式验证
表1汇总了压差施肥罐施肥试验的相关参数[13-20]并对不同作者的试验进行编号,其中出口肥液浓度的初始值0(0)通过/(+)计算,为水的密度。通过表1中相关文献报道的实测数据,图4对比了出口肥液浓度的试验值与式(5)、式(7)~(9)的计算值,其中虚线是2倍偏差线。在应用压差施肥罐进行施肥时,0()/0(0)达到e-4时可以基本认为施肥过程结束[21],因此图4中坐标的取值范围为[e-4, e0]。

表1 压差施肥罐施肥试验参数汇总
图4a中式(5)对不同试验组处于[e-4, e0]区间的出口浓度的预测基本围绕在试验值附近,只有对少数试验值的预测在2倍偏差以外。处于2倍偏差外的试验值主要集中在[e-4, e-2]区间内,此时0()/0(0)已经处于10-2数量级,式(5)的计算出现偏离的原因可能是试验过程中低肥液浓度的数据采集存在误差。图4b中式(7)对①②④试验组处于[e-4, e0]区间的试验值存在较为明显的低估。由于式(7)的推导中认为水肥瞬间混合均匀且无肥料的溶解过程[11],因此式(7)适用于试验中水肥混合较为均匀、肥料溶解过程不存在或存在时间较短的③⑤⑥试验组。而①②④试验组存在明显肥料溶解使出口肥液浓度的实际衰减过程比式(7)更慢。

注:实线代表计算值与试验值相等;虚线为2倍偏差线;y为C0(t)/ C0(0)试验值;y′为C0(t)/ C0(0)计算值。
图4c和图4d中式(8)~式(9)对部分试验组出口肥液浓度的计算不够准确,如式(8)对试验组③⑤⑥的预测;式(9)对试验组②③④⑥中部分试验值的预测。式(8)~式(9)是基于作者试验结果的拟合式[6,13],其中指数的拟合并非基于量纲分析因而无法排除其他变量影响,因此对于部分试验组的计算结果不够准确。综合图4的结果,与式(7)~式(9)相比,考虑肥料溶解过程的出口肥液浓度理论公式(式(5))适用于不同的施肥试验和施肥工况并实现了较为准确的出口肥液浓度预测。
表2提供了图4中式(5)、式(7)~式(9)计算准确性的定量评价,使用了计算效果评估中常用的5个指标[28-29],其中MAE是平均绝对偏差;RMSE是均方差;MG是几何平均偏差;VG是几何方差;FAC2是2倍偏差之间的预测分数。当各时刻计算值与试验值均相等时,MAE=0、RMSE=0、MG=1、VG=1、FAC2=100%。但通常当计算结果的评估指标满足0.70
式(5)计算的MAE、RMSE、MG、VG和FAC2的平均值分别为0.04、0.06、0.89、1.19和88.26%,对不同试验组基本满足评估指标的范围要求,说明式(5)能够较准确地预测出口浓度。式(7)对应的MG和VG的平均值分别为1.78(>1.30)和3.82,出现偏离的原因是式(7)对试验组①②④出口浓度的计算出现了低估(图 4b)。式(8)对应的MG和VG的平均值分别为2.47(>1.30)和21.09,出现偏离的原因是式(8)对试验组③⑤⑥的计算存在较明显的低估(图4c)。式(9)对应的MG和VG的平均值分别为0.58(<0.70)和7.31,出现偏离的原因是式(9)对试验组②③④⑥部分试验值的计算存在高估(图4d)。式(5)、式(7)~式(9)对应的FAC2的平均值均大于50%。但对于部分试验组,如式(7)、式(9)对试验组②的计算和式(8)对试验组⑥的计算,出现了FAC2为20%~40%的结果。这同样说明式(7)~式(9)对部分试验组的计算存在较大偏差。表2的定量评价结果表明,对于表1中的6组施肥试验,式(5)的计算性能优于式(7)~式(9)。
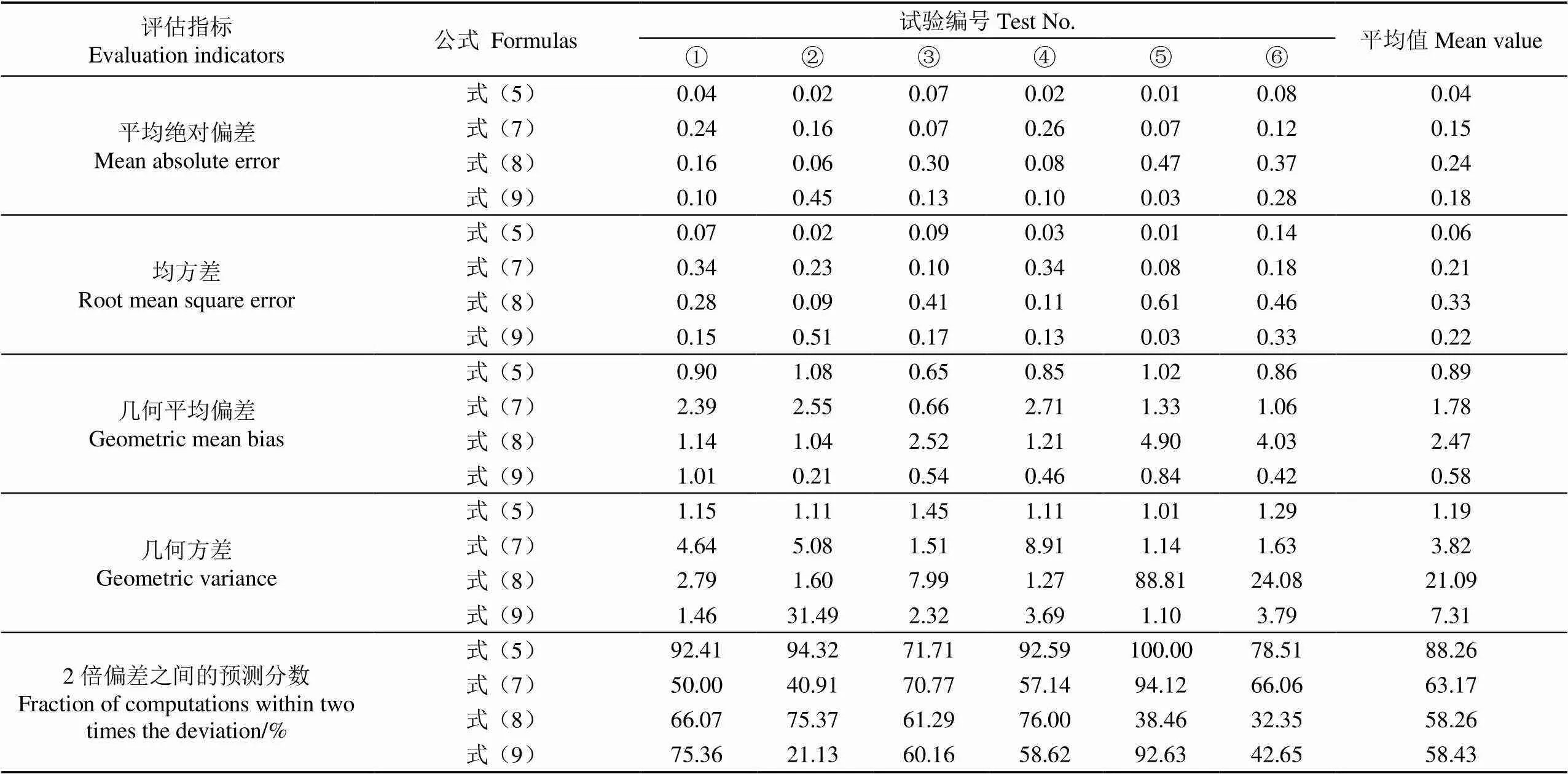
表2 式(5)、式(7)~式(9)计算准确性的定量评价
6组施肥试验中试验组①②④存在较明显的肥料溶解过程,而试验组③⑤⑥在施肥过程中肥料溶解现象不存在或存在时间很短。表3选取了各试验组中的典型工况并列出了各工况的相关参数,各工况对应的和列在表中。
图5对比了各工况无量纲源项随无量纲时间的变化过程。工况5的0变化过程与工况3类似,工况6的0恒等于0(=0),即不存在肥料的溶解过程,因此工况5和工况6图形省略。工况1(图5a)0的初始值为0(0)(=1.00),但0的衰减速度很快(=0.91),在/=1时基本衰减至0。工况4(图5d)0初始值同样为0(0)(=1.00),但0的衰减速度较慢(=0.43),在/=3时基本衰减至0。工况2(图5b)0初始值为0.270(0)(=0.27),且衰减速度很慢(=0.06)。在/=0~4时间段内0从0.270(0)近似线性地减小至0.110(0),说明在该时段内长期存在一定程度的肥料溶解。工况1、工况2和工况4对应的0随时间的变化过程说明试验组①②④的试验过程中存在较明显的肥料溶解。肥料溶解量的多少和溶解过程存在时间的长短与具体施肥试验参数有关。工况3(图5c)0的初始值为0.080(0),且0的衰减速度很快(=0.78),在/=1时基本衰减至0。工况3、工况5和工况6中0的变化过程说明试验组③⑤⑥的试验过程中肥料溶解量较小、溶解过程存在时间较短或不存在肥料的溶解。
图6对比了/=0−4时间段内各工况无量纲的出口肥液浓度的试验值与式(5)、式(7)~(9)的计算值。在施肥过程时,单位时间流出压差施肥罐的肥料总量为0(),单位时间肥料的溶解总量为0()。当0()<0()时,肥料的溶解会使出口肥液浓度不断升高,直至0()=0()。考虑到0(0)≥0(0)(0≤≤1),因此0()<0()的情况在实际施肥过程中不会出现。相反,当0()>0()时,由于流出的肥料量大于溶解的肥料量,此时,出口肥液浓度便会不断降低。当0()=0()时,此时流出的肥料量与溶解的肥料量相等,压差施肥罐内溶于水的肥料总量处于动态平衡状态,出口肥液浓度保持恒定。工况1(图 6a)0在施肥初始阶段衰减较慢,随后衰减较为迅速,这与工况1的0初始值较大但衰减迅速的变化过程对应(图 5a)。与工况1相比,工况4(图6d)0的衰减速度较慢,这与工况4的0初始值较大且衰减较慢的变化过程一致(图5d)。工况2(图 6b)0在施肥初始阶段衰减较快,随后的衰减逐渐变缓,这与图5c中工况2的0初始值较小但衰减速度很慢保持一致。对于工况2,当0减小至0.20(0)时(/=1.5),相应的0=0.190(0),在此后的一段时间内(/=1.5−4)0()与0()的大小非常接近,因此0在这段时间内比较稳定,变化幅度很小。而工况3(图6c)、工况5和工况6中由于肥料溶解量较小、溶解过程存在时间较短或不存在肥料溶解,因此式(5)的计算值与式(7)相比非常接近或完全相等。与图4中的对比结果一致,式(7)对工况1、工况2和工况4试验值的预测存在较明显的低估,其原因是式(7)没有考虑施肥过程中的肥料溶解。拟合式(8)~式(9)由于不是基于量纲分析的拟合,并且只考虑了各自研究中的施肥试验,因此对部分工况试验值的预测也存在一定程度的高估或低估。式(8)由于只考虑了施肥量和压差2个因素,因此出现的预测偏差更为明显。
表3中工况1~6式(5)、式(7)~(9)计算值对应的MAE平均值分别为0.020、0.102、0.127和0.124。式(7)~式(9)的MAE平均值是式(5)的5.1、6.4和6.2倍,这说明对于部分工况式(7)~式(9)的计算偏差较为明显。与式(7)~式(9)相比,式(5)可以合理地描述肥料溶解对出口肥液浓度的影响,进而能够实现对不同时刻出口肥液浓度的准确计算。

表3 各试验组典型工况参数汇总
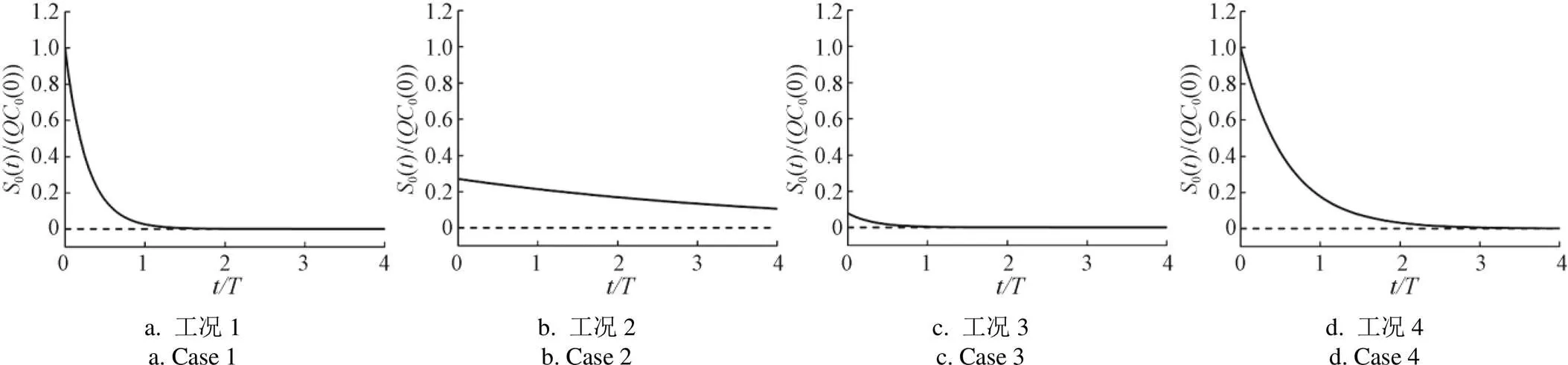
图5 不同工况S0(t)/(QC0(0)) 随时间的变化

图6 不同工况C0(t)/C0(0)随时间的变化
3 考虑肥料溶解的均匀施肥
关于压差施肥罐的均匀施肥方法,已经开展了相关工作[22]。但该方法基于肥料完全溶解并且水肥混合均匀的条件下通过流量控制实现。当罐体内存在肥料溶解时,流量的变化会对罐内的水肥混合和肥料的溶解过程产生影响,因此均匀施肥方法的理论推导难度将会大大增加。考虑到=1、=0时,式(4)~式(5)均为常数,即0()=0(0)=0()。流出的肥料量与溶解的肥料量相等,罐内肥液浓度饱和且有充足的肥料可供长期溶解施肥。对于该特殊解,可以建立考虑肥料溶解过程的均匀施肥方法,如图7所示。当=1、=0时出口肥液浓度恒为0(0),此时只需满足(+0)C=0(0),即0=(0(0)-C)/C,便可实现施肥流量为+0、施肥浓度为C的均匀施肥过程。但在实际生产中,压差施肥罐体积通常较小,化肥的水溶性也存在差异。因此需要设计生产专用的体积较大的压差施肥罐,并使用水溶性好的化肥,以实现罐内肥液浓度饱和且有充足的肥料可供长期溶解施肥这一特殊工况。

注:Q0为流过主管道的流量,m3·s-1;Cu为均匀施肥的最优浓度,%。
4 结 论
为了更准确地描述压差施肥罐出口肥液浓度的变化过程,本研究推导了考虑肥料溶解的出口肥液浓度理论公式,并初步探讨了考虑肥料溶解的均匀施肥方法。主要结论如下:
1)基于含源项的肥料输移扩散连续方程推导得到了出口肥液浓度变化的微分方程,并引入参数描述肥料溶解过程对压差施肥罐出口肥液浓度的影响,得到了出口肥液浓度变化的理论公式。通过与现有试验数据对比,理论公式计算结果的平均绝对偏差、均方差、几何平均偏差、几何方差和两倍偏差之间的预测分数的平均值分别为0.04、0.06、0.89、1.19和88.26%,验证了理论公式对出口肥液浓度的计算准确性。当参数取特定值时,理论公式可以转化为目前广泛应用的压差施肥罐出口肥液浓度的负指数公式。与负指数公式及试验拟合公式相比,本文提出的理论公式可以合理地描述肥料溶解对出口肥液浓度的影响,进而能够实现对出口肥液浓度的准确计算。
2)当罐内肥液浓度持续饱和且有充足的肥料可供长期溶解施肥时,提出了考虑肥料溶解过程的均匀施肥方法,用于指导压差施肥罐实现均匀施肥。此时只需设定适宜的主管道流量,便可实现恒定施肥流量和最优浓度的均匀施肥过程。但通常情况下,罐内肥液浓度无法持续饱和,肥料的溶解也会随时间不断变化,考虑这些因素的均匀施肥方法有待进一步研究。
[1]Kang S Z, Hao X M, Du T S, et al. Improving agricultural water productivity to ensure food security in China under changing environment: From research to practice[J]. Agricultural Water Management, 2017, 179: 5-17.
[2]钟茜,巨晓棠,张福锁. 华北平原冬小麦/夏玉米轮作体系对氮素环境承受力分析[J]. 植物营养与肥料学报,2006,12(3):285-293. Zhong Xi, Ju Xiaotang, Zhang Fusuo. Analysis of environmental endurance of winter wheat/summer maize rotation system to nitrogen in North China Plain[J]. Plant Nutrition and Fertilizer Science, 2006, 12(3): 285-293. (in Chinese with English abstract)
[3]Bai X G, Wang Y N, Huo X X, et al. Assessing fertilizer use efficiency and its determinants for apple production in China[J]. Ecological Indicators, 2019, 104: 268-278.
[4]Zhang X, Bol R, Rahn C, et al. Agricultural sustainable intensification improved nitrogen use efficiency and maintained high crop yield during 1980-2014 in Northern China[J]. Science of the Total Environment, 2017, 596-597: 61-68.
[5]Kaplan M, Kara K, Unlukara A, et al. Water deficit and nitrogen affects yield and feed value of sorghum sudangrass silage[J]. Agricultural Water Management, 2019, 218: 30-36.
[6]孟一斌,李久生,李蓓. 微灌系统压差式施肥罐施肥性能试验研究[J]. 农业工程学报,2007,23(3):41-45. Meng Yibin, Li Jiusheng, Li Bei. Fertilization performance of the pressure differential tank in micro-irrigation system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(3): 41-45. (in Chinese with English abstract)
[7]汪小珊,严海军,周凌九,等. SSQ系列射流施肥器水力性能的试验研究[J]. 农业工程学报,2020,36(21):31-38. Wang Xiaoshan, Yan Haijun, Zhou Lingjiu, et al. Experimental research of hydraulic performance on jet fertilizer applicator of SSQ series[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 31-38. (in Chinese with English abstract)
[8]李久生,杜珍华,栗岩峰. 地下滴灌系统施肥灌溉均匀性的田间试验评估[J]. 农业工程学报,2008,24(4):83-87. Li Jiusheng, Du Zhenhua, Li Yanfeng. Field evaluation of fertigation uniformity for subsurface drip irrigation systems[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(4): 83-87. (in Chinese with English abstract)
[9]李建明,于雪梅,王雪威,等. 基于产量品质和水肥利用效率西瓜滴灌水肥制度优化[J]. 农业工程学报,2020,36(9):75-83. Li Jianming, Yu Xuemei, Wang Xuewei, et al. Optimization of fertigation scheduling for drip-irrigated watermelon based on its yield, quality and fertilizer and water use efficiency[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(9): 75-83. (in Chinese with English abstract)
[10]Li J S. Increasing crop productivity in an eco-friendly manner by improving sprinkler and micro-irrigation design and management: A review of 20 years’ research at the IWHR, China[J]. Irrigation and Drainage, 2017, 67(1): 97-112.
[11]封俊,沈雪民,刘春和,等. 压差式喷灌施肥装置的研究[J]. 农业工程学报,1991,7(2):107-113. Feng Jun, Shen Xuemin, Liu Chunhe, et al. A study on the pressure differential fertilizer injection unit in sprinkler irrigation system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 1991, 7(2): 107-113. (in Chinese with English abstract)
[12]李凯,毛罕平,李百军. 混药混肥装置控制性能分析[J]. 农业机械学报,2003,34(1):50-53. Li Kai, Mao Hanping, Li Baijun. Analysis on control performance of various pesticide or fertilizer mixers[J]. Transactions of the Chinese Society for Agricultural Machinery, 2003, 34(1): 50-53. (in Chinese with English abstract)
[13]Li J S, Meng Y B, Liu Y. Hydraulic performance of differential pressure tanks for fertigation[J]. Transaction of the ASABE, 2006, 49(6): 1815-1822.
[14]邓兰生,张承林,郭彦彪. 压差施肥罐施肥时间解析[J]. 节水灌溉,2007(3):26-28,31. Deng Lansheng, Zhang Chenglin, Guo Yanbiao. Analysis of fertilization time in differential pressure tank[J]. Water Saving Irrigation, 2007(3): 26-28, 31. (in Chinese with English abstract)
[15]韩启彪. 设施农业灌溉施肥器性能试验研究[D]. 北京:中国农业大学,2008. Han Qibiao. Experimental Study on Performances of Fertigation Injectors in Agricultural Facilities[D]. Beijing: China Agricultural University, 2008. (in Chinese with English abstract)
[16]陈剑,吕新. 滴灌棉田压差式施肥罐注肥均匀度研究与分析[J]. 节水灌溉,2011(1):62-64. Chen Jian, Lü Xin. Study on fertilization uniformity of pressure differential tank in drip irrigation cotton field[J]. Water Saving Irrigation, 2011(1): 62-64. (in Chinese with English abstract)
[17]范军亮,张富仓,吴立峰,等. 滴灌压差施肥系统灌水与施肥均匀性综合评价[J]. 农业工程学报,2016,32(12):96-101. Fan Junliang, Zhang Fucang, Wu Lifeng, et al. Field evaluation of fertigation uniformity in drip irrigation system with pressure differential tank[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 96-101. (in Chinese with English abstract)
[18]Fan J L, Wu L F, Zhang F C, et al. Evaluation of drip fertigation uniformity affected by injector type, pressure difference and lateral layout[J]. Irrigation and Drainage, 2017, 66(4): 520-529.
[19]杨欣. 滴灌系统压差式施肥装置性能及施肥均匀性研究[D]. 杨凌:西北农林科技大学,2017. Yang Xin. Study on Performance and Fertilizer Uniformity of Differential Pressure Fertilizer Apparatus in Drip Irrigation System[D]. Yangling: Northwest Agricultural and Forest University, 2017. (in Chinese with English abstract)
[20]杨欣,王文娥,胡笑涛,等. 滴灌系统压差式施肥罐施肥性能研究[J]. 节水灌溉,2017(10):79-83. Yang Xin, Wang Wene, Hu Xiaotao, et al. Study on fertilization performance of drip irrigation system with pressure differential tank[J]. Water Saving Irrigation, 2017(10): 79-83. (in Chinese with English abstract)
[21]韩启彪,李浩,冯绍元,等. CFD模拟在压差施肥罐浓度衰减研究中的应用初探[J]. 灌溉排水学报,2015,34(12):81-84. Han Qibiao, Li Hao, Feng Shaoyuan, et al. Preliminary application of CFD simulation technology to concentration decay law research of pressure-fertilizer tank[J]. Journal of Irrigation and Drainage, 2015, 34(12): 81-84. (in Chinese with English abstract)
[22]胡昕宇,严海军,陈鑫. 基于压差式施肥罐的均匀施肥方法[J]. 农业工程学报,2020,36(1):119-127. Hu Xinyu, Yan Haijun, Chen Xin. Uniform fertilization method based on differential pressure tank[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(1): 119-127. (in Chinese with English abstract)
[23]Chau K W, Jiang Y W. Three-dimensional pollutant transport model for the Pearl River Estuary[J]. Water Research, 2002, 36(8): 2029-2039.
[24]Dokoumetzidis A, Papadopoulou V, Macheras P. Analysis of dissolution data using modified versions of Noyes-Whitney equation and the Weibull function[J]. Pharmaceutical Research, 2006, 23(2): 256-261.
[25]Rindt D W, Blouin G M, Getsinger J G. Sulfur coating on nitrogen fertilizer to reduce dissolution rate[J]. Journal of Agricultural and Food Chemistry, 1968, 16(5): 773-778.
[26]童菊秀,杨金忠,暴入超. 土壤中溶解性溶质流失特征试验[J]. 农业工程学报,2010,26(6):77-82. Tong Juxiu, Yang Jinzhong, Bao Ruchao. Characteristics of soluble chemical loss in soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(6): 77-82. (in Chinese with English abstract)
[27]Burt C, Connor K O, Ruehr T. Fertigation[M]. San Luis Obispo: Irrigation Training and Research Center, California Polytechnic State University, 1998.
[28]Pan Y, Chamecki M, Isard S A. Large-eddy simulation of turbulence and particle dispersion inside the canopy roughness sublayer[J]. Journal of Fluid Mechanics, 2014, 753: 499-534.
[29]刘艳芳,宋玉玲,郭龙,等. 结合高光谱信息的土壤有机碳密度地统计模型[J]. 农业工程学报,2017,33(2):183-191. Liu Yanfang, Song Yuling, Guo Long, et al. Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 183-191. (in Chinese with English abstract)
[30]Gleicher S C, Chamecki M, Isard S A, et al. Interpreting three-dimensional spore concentration measurements and escape fraction in a crop canopy using a coupled Eulerian-Lagrangian stochastic model[J]. Agricultural and Forest Meteorology, 2014, 194: 118-131.
Calculation method of fertilizer concentration at outlet based on differential pressure tank considering fertilizer dissolution
Hu Xinyu, Yan Haijun, Chen Xin※
(1.,,100083,; 2.,,100083,)
Differential pressure tank is widely used in the fertigation technology in China because of its low cost, simple and convenient. In this study, a theoretical formula was derived for the fertilizer concentration at outlet based on differential pressure tank considering fertilizer dissolution. The continuity equation for fertilizer transportation and diffusion with source term was used to obtain the differential equation for the fertilizer concentration at outlet. The influence of fertilizer dissolution on the fertilizer concentration at outlet was described by parameters considering the actual process of fertilizer dissolution, and the theoretical formula was obtained for the fertilizer concentration at outlet. In the theoretical formula, one parameter represented the initial dissolution rate of fertilizer in the tank, and the other parameter described the decreasing speed of fertilizer dissolution rate in the tank. When the parameters in the theoretical formula took a specific value, the theoretical formula could be transformed into the classical exponential formula of fertilizer concentration. The variations of source term and fertilizer concentration at outlet with time were further discussed when the parameters took different values. Compared with the experimental data, the theoretical formula considering fertilizer dissolution was suitable for different fertilization experiments and fertilization conditions, and achieved more accurate prediction for fertilizer concentration at outlet than the classical exponential formula and the experimental regression formulas. The classical exponential formula was obviously underestimated for the fertilization experiments with obvious fertilizer dissolution, and the experimental regression formulas were also overestimated or underestimated to some extent for some experimental results. The average values of mean absolute error, root mean square error, geometric mean bias, geometric variance and the fraction of computations within two times the deviation for the theoretical formula were 0.04, 0.06, 0.89, 1.19 and 88.26%, respectively, which verified the accuracy of the theoretical formula for the prediction of fertilizer concentration at outlet. For the classical exponential formula and the experimental regression formulas, the average values of geometric mean bias and geometric variance deviated from the reasonable range, and the deviation for some experiments was very distinct. The average mean absolute error of the theoretical formula for typical cases was 0.020. The mean absolute errors for the classical exponential formula and the experimental regression formulas were 0.102, 0.127 and 0.124, which were 5.1, 6.4 and 6.2 times of the theoretical formula. On this basis, the uniform fertilization method under differential pressure tank was further illustrated considering fertilizer dissolution when the fertilizer concentration in the tank was saturated continuously and the sufficient fertilizer was supplied for long-term dissolution and fertilization. The fertilizer amount dissolved in the tank was always equal to the fertilizer amount flowing out of the tank in this particular case. At this point, the uniform fertilization of constant fertilization flux and optimal fertilizer concentration can be realized by setting an appropriate main pipe flux. The theoretical formula considering fertilizer dissolution calculates the fertilizer concentration at outlet precisely, and provides a feasible scheme for uniform fertilization under differential pressure tank.
fertilizers; dissolution; fertigation; differential pressure tank; concentration at outlet; theoretical formula; uniform fertilization
胡昕宇,严海军,陈鑫. 考虑肥料溶解的压差施肥罐出口肥液浓度计算方法[J]. 农业工程学报,2020,36(24):99-106.doi:10.11975/j.issn.1002-6819.2020.24.012 http://www.tcsae.org
Hu Xinyu, Yan Haijun, Chen Xin. Calculation method of fertilizer concentration at outlet based on differential pressure tank considering fertilizer dissolution[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(24): 99-106. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2020.24.012 http://www.tcsae.org
2020-08-10
2020-11-11
国家重点研发计划项目(2017YFD0201502);国家自然科学基金资助项目(51836010、41961144014)
胡昕宇,博士生,主要从事灌溉施肥设备与水肥流动研究。Email:huxinyu@cau.edu.cn
陈鑫,研究员,博士生导师,主要从事灌溉施肥技术与两相流动研究。Email:chenx@cau.edu.cn
10.11975/j.issn.1002-6819.2020.24.012
S147.3
A
1002-6819(2020)-24-0099-08
