考虑不确定性的模块化战术导弹优化设计

刘钧圣， 王刚， 王琨， 史宏博， 郭斌

(1.西北工业大学 航天学院, 陕西 西安 710072; 2.西安现代控制技术研究所, 陕西 西安 710065)

0 引言

依托于武装直升机平台，直升机载空地导弹具有机动性强、作战距离远、杀伤威力大、命中精度高等特点，是最重要、最有效的反装甲武器之一。目前，直升机载空地导弹发展的一个方向是模块化、系列化[1]，即弹体采用分舱段模块化结构安装方式，可依据军方使用需求，针对不同制导体制的导引头(如：图像类、激光类、雷达类、复合制导类)与战斗部(如：破甲杀伤型、温压型、侵彻型)，灵活快速地将其组装在一起，便于部队作战使用[2]。模块化导弹具有成本低、各部件功能独立性强、便于检测维修与故障定位等优点。

然而在模块化导弹设计过程中，由于存在多种组合方式，使其有效载荷、质心位置均在一定范围内浮动，受环境影响其实际飞行速度与设计值也可能不同；另一方面，在工程研制过程中，导弹弹道参数(飞行高度、弹道倾角等)设计，会根据飞行试验后的真实气动参数、扰动与干扰力矩等进行调整。上述不确定性因素会导致采用传统确定性优化得到的设计结果无法满足设计要求。国内外众多学者曾探讨和总结了考虑不确定性的大型导弹或飞行器设计方法与设计准则。陈建江等[3]建立了基于神经网路的飞航导弹稳健性优化设计模型，设计结果显示增大助推器有助于提高不确定性因素对主级导弹射程的影响。马英等[4]将不确定性设计理论应用于空射巡航导弹概念设计中，研究表明：设计参数波动5%，稳健性方案的射程波动幅度比确定性最优方案减小了61%，最大飞行速度波动幅度减小了57%。Jaeger等[5]针对飞机概念设计阶段存在的总体参数不确定性，利用二次响应面代理模型进行了不确定性分析，结果表明：通过增大机翼展弦比与后掠角，使飞机满足滑跑距离、航程、弹翼展长等约束的概率得到了显著提升，但付出了稍许质量代价。目前关于小型战术导弹的不确定性设计研究很少。刘常青等[6]以200 kg级别防空导弹为研究对象，建立了基于偏差量的导弹总体方案设计模型。基于原型弹，拟定一组设计变量并给出统计得到的概率分布，然后通过MATLAB/Simulink弹道仿真得出导弹性能及相关约束条件。仿真结果表明：导弹推力、发射初始角、助推段末速对导弹质量与射程影响较为敏感。小型战术导弹设计时具有自身的特殊性，其有效载荷、质心位置、飞行速度等参数对其翼载荷、推重比、发动机装药、静稳定度等影响较为敏感，如果抛开上述不确定性因素去设计模块化导弹，会导致导弹实际的飞行性能偏离确定性优化最优解很多，同时设计约束也无法满足。

针对上述问题，本文以某型模块化直升机载空地导弹为研究对象，将稳健性优化设计理论[7-9]融入导弹总体设计原理中，建立模块化战术导弹稳健性优化设计模型，旨在解决满足设计约束条件下，减小载荷质量与质心位置、飞行速度、弹道方案3类不确定性因素对模块化导弹起飞质量影响这一问题，并依据稳健性优化结果，提出模块化直升机载空地导弹总体参数稳健性设计准则。

1 直升机载空地导弹总体方案

某型模块化直升机载空地导弹用于打击地面坦克、车辆、工事及有生力量，它以裸弹的形式挂载于直升机发射架上，起飞质量不超过38 kg，射程2～10 km，需用过载≥5g，g为重力加速度。导弹总体方案如图1所示，采用正常式X-X气动布局、大展弦比平直矩形弹翼(发射前弹翼向后折叠，发射后弹翼按固定时序张开)，两级双室双推固体火箭发动机为导弹提供助推与续航，助推发动机不与导弹分离。弹体各舱段为模块化设计方案，导引头舱与引战舱可根据作战需求进行更换。

考虑到武装直升机对导弹起飞质量有着严苛的要求，本方案在满足射程、需用过载条件下，通过减小续航发动机装药，使导弹在末端以无动力滑翔方式来攻击地面目标，来减小导弹质量，速度曲线(速度v与时间t的关系)和弹道方案(发射系y轴向位移与x轴向位移的关系)分别如图2、图3所示。图2中：tb为助推发动机工作结束时刻，vb为tb时刻对应的导弹速度；ts为续航发动机工作结束时刻，vs为ts时刻对应的导弹速度；te为导弹命中目标时刻，ve为te时刻对应的导弹速度，即导弹末速。图3中：H为导弹中制导段飞行高度，θc为导弹爬升段弹道倾角，θg为导弹俯冲段弹道倾角。

图2 速度曲线Fig.2 Velocity characteristic

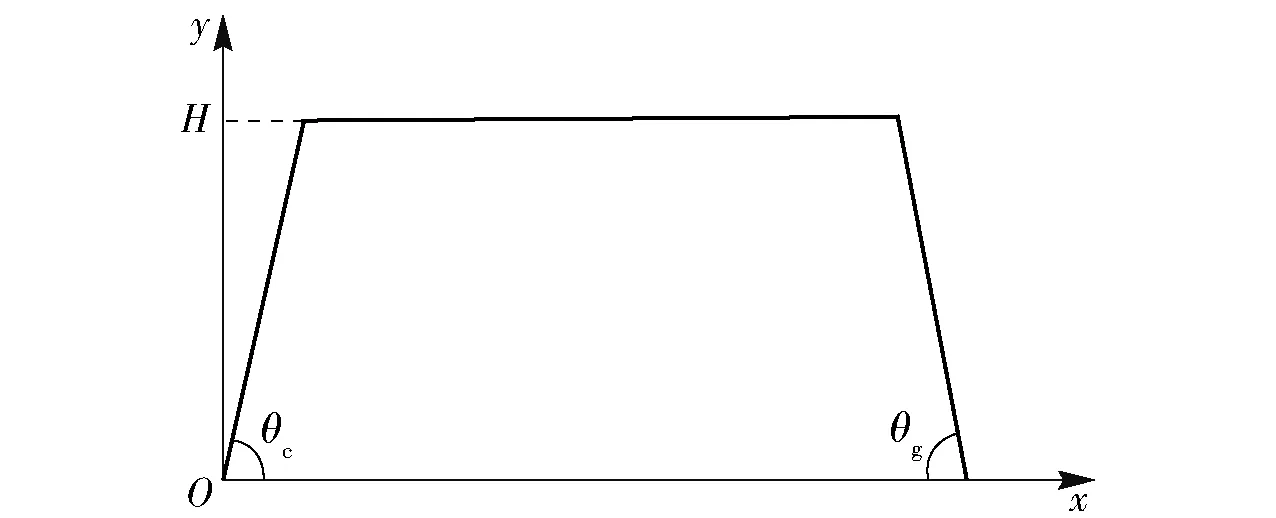
图3 弹道方案Fig.3 Flight trajectory profile

2 直升机载空地导弹稳健性优化设计

与传统确定性优化相比，稳健性优化设计最大的特点是要进行不确定性分析，计算目标的均值与方差。不确定性分析的经典方法为蒙特卡洛仿真(MCS)，具有计算简单、精度高等特点。应用MCS需要样本量要足够大，考虑到本文导弹总体设计时，迭代计算气动力较为耗时，不可能直接将MCS应用于导弹稳健性优化设计中。为此，引入Kriging代理模型解决该问题。

构建的导弹稳健性优化设计框架如图4所示，包括导弹总体设计、代理模型与稳健性优化三部分，整个计算程序在MATLAB环境[10]中实现。具体优化设计流程为：

1) 定义稳健性优化问题，包括设计变量、不确定性变量/参数、优化目标、约束条件等；

2) 建立导弹总体设计模型，依据定义的设计变量评估外形参数、气动力、动力特性、弹道方程以及导弹质量。如果前后两次导弹质量差小于0.05 kg，则认为程序收敛，输出性能与约束条件，否则更新外形参数进行迭代；

3) 利用试验设计生成样本点，然后根据建立的总体设计模型对样本点进行分析，得到一组输入/输出，基于该组数据选用近似方法构建代理模型，如果代理模型精度未达到指定值，则添加样本点直至满足精度；

4) 对代理模型进行MCS不确定性分析，计算目标函数的均值与方差，再利用多目标优化算法求解Pareto解集，根据偏好选取设计方案。

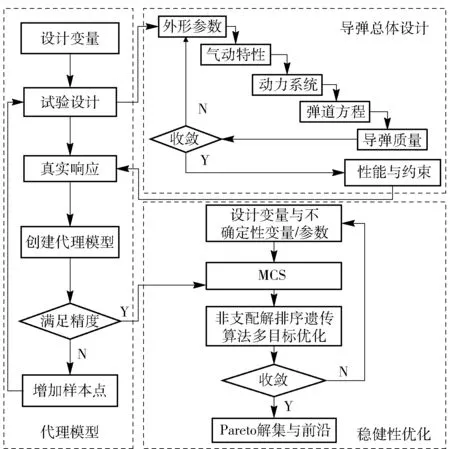
图4 导弹稳健性优化设计框架Fig.4 Optimization framework for missile robust design

2.1 稳健性优化设计

某模块化直升机载空地导弹标称有效载荷mp=15 kg，标称静稳定度K=8.5%. 表1列出了设计变量及取值范围，表2给出了约束定义及范围。图5给出了与设计变量和约束相关的参数定义，图中：l为导弹长度，lk为质心与焦点之间的距离，lwf为弹翼前缘与尾舵前缘之间的距离，bw为弹翼展长，bf为尾舵展长，cw为弹翼弦长，AR为弹翼展弦比。

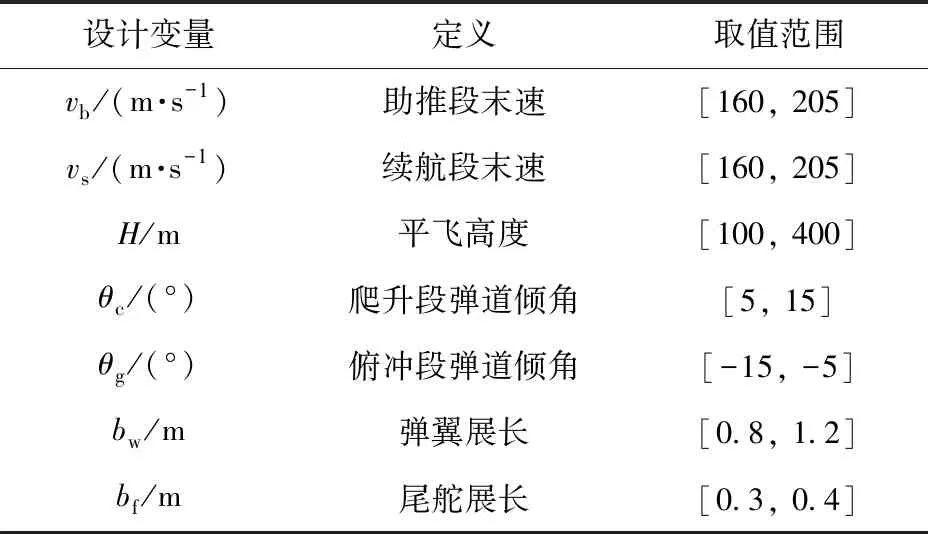
表1 设计变量的定义及取值范围Tab.1 Definition and value range of design variables

基于前文论述的模块化导弹不确定性因素，确定了如表3所示的3类不确定性问题。

表2 约束的定义与范围Tab.2 Definition and range of constraints

图5 导弹外形参数定义Fig.5 Definition of missile layout

表3 3类不确定性优化问题描述

Tab.3 Description of 3 uncertainty problems

不确定性问题涉及变量与参数概率分布类型载荷质量mp/kg服从均匀分布[13, 16]质心位置K/%服从均匀分布[6, 11]速度方案vb/(m·s-1)在设计值处,服从正态分布,标准差为8vs/(m·s-1)在设计值处,服从正态分布,标准差为8弹道方案H/m在设计值处,服从正态分布,标准差为20θc/(°)在设计值处,服从正态分布,标准差为1θg/(°)在设计值处,服从正态分布,标准差为1

该导弹稳健性优化是在满足射程Dr=10 km、需用过载nr=5g条件下，考虑上述3类不确定性问题，通过求解表1中的设计变量，使导弹质量均值μmt与标准差σmt最小。为避免由于不确定性因素变化而导致约束无法满足，对约束进行概率性描述，均取90%. 优化问题可描述为：

Set 表3中的3类不确定性问题，

Findx=[vb,vs,H,θc,θg,bw,bf]T，

Min [μmt,σmt]T,

采用描述性取样策略，样本均值与方差的计算公式为

(1)

式中：N为样本点个数，设定为50 000；mi为第i个随机样本点的质量。由(1)式易知，稳健性优化设计为多目标优化问题，本文采用非支配解排序遗传算法(NSGA-Ⅱ)[11-12]求解该问题，设定NSGA-Ⅱ优化算法的初始种群为300，种群进化代数为500.

2.2 导弹总体设计

2.2.1 外形参数

导弹外形参数包括弹长、弹径、弹翼展长与弦长、尾舵展长与弦长。其中，弹径参考基准导弹与战斗部威力定为0.14 m，弹长根据基准导弹结合发动机装药形式、装药质量及装药密度进行估算。此处只需计算弹翼与尾舵尺寸。弹翼尺寸由(2)式确定：

(2)

式中：mm为主级(续航)导弹质量；pm为主级导弹翼载荷；S为弹翼参考面积。pm与mm将在后续推进系统与质量模块中分别计算。尾舵面积则由需用过载nr与最大配平舵偏角(取20°)来确定。

2.2.2 气动特性

采用涡格法(VLM)[13]计算导弹升力、焦点、诱导阻力、尾舵效率。引入普朗特- 格劳厄脱压缩性修正因子来计算亚声速状态下的翼面升力。图6(a)显示了利用VLM建模后的导弹几何外形，弹翼和尾舵在建模时均分为内外两部分，内侧代表与弹身的融合区，外侧代表单独的翼面，其中尾舵外侧区域可以偏转。图6(b)显示了该导弹在马赫数Ma=0.3，攻角α=2°，舵偏角δ=-4°条件下的压力云图。

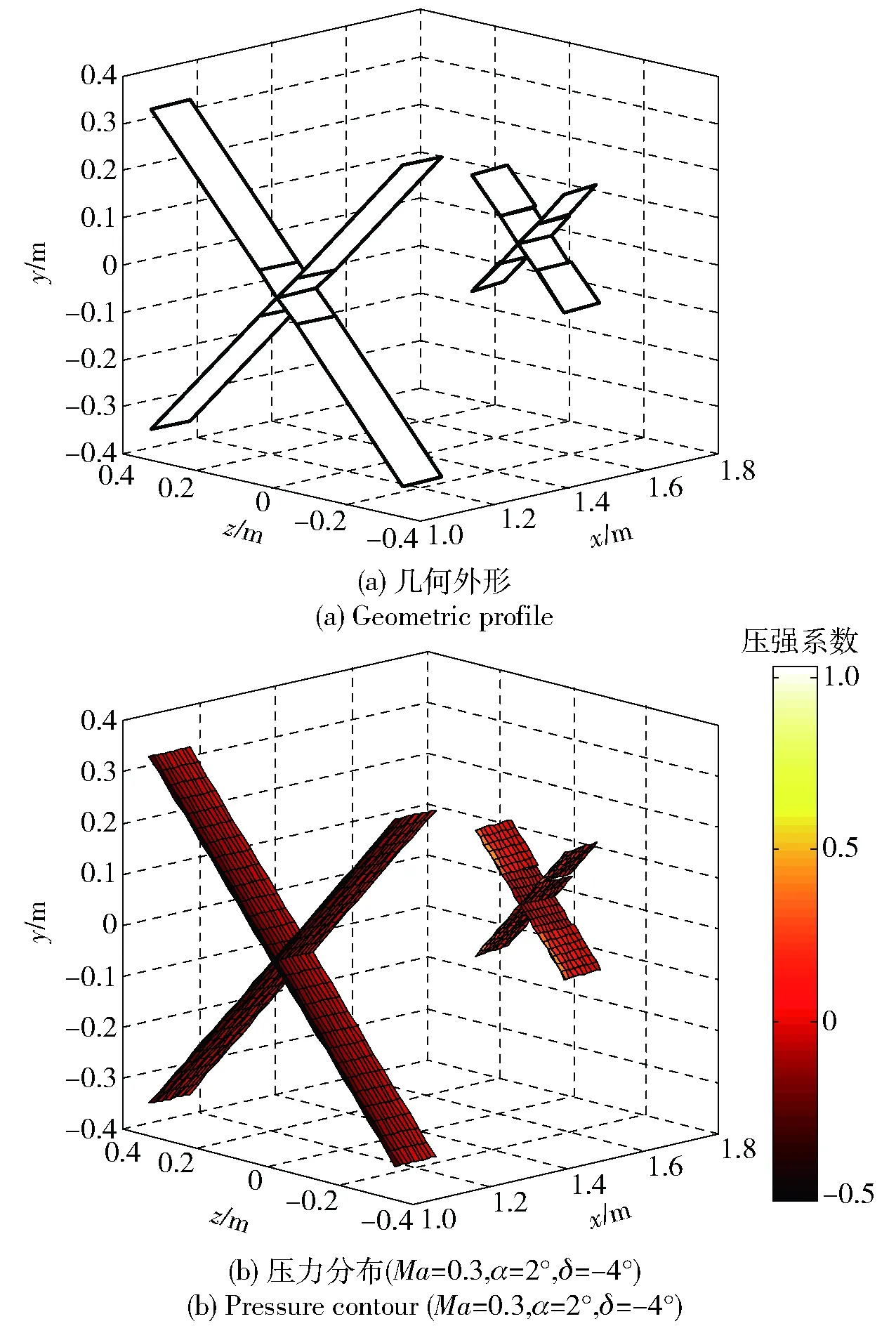
图6 VLM对X-X布局导弹建模Fig.6 Modeling X-X configuration missile by VLM

阻力计算基于部件叠加的原理，将全弹阻力分解为弹翼阻力和弹身阻力。亚声速弹翼阻力由诱导阻力和型阻组成，诱导阻力由VLM直接得出，型阻则通过基于XFOIL二维翼型数据的片条理论来预测[14]；弹身阻力由摩擦阻力、压差阻力和底部阻力构成，全部根据工程估算法[15]来计算。

基于VLM的气动力计算方法，将全弹划分为 480个网格，利用Intel Xeon 2.80 GHz电脑运算，每计算一组气动力(升阻力系数关于马赫数与攻角的数据)耗时约56 s. 该方法与风洞试验对比结果表明：当Ma在0.3～0.6，攻角在0～8°范围时，各气动参数最大计算误差[16]在12%以内，可满足概念设计阶段所需。

2.2.3 推进系统

参考成熟型号，助推级发动机比冲Ib≈220 s，续航级发动机比冲Is≈190 s.

2.2.3.1 助推发动机主要参数

工作时间tb：

(3)

式中：nxmax为导弹最大轴向过载，取20g. 将助推发动机燃料质量mb与导弹起飞质量mt的比值定义为助推发动机燃料质量相对因数μb[17]：

(4)

则

(5)

式中：X为阻力；Tb为助推发动机推力；由于助推段推力远大于阻力，可取ξ=1. 将(3)式中的tb代入(5)式，可得μb.

2.2.3.2 续航发动机主要参数

(6)

式中：v为导弹飞行速度；Cx为阻力系数；θ为弹道倾角；ρ为空气密度；p为该时段的翼载荷。由(6)式可知，为计算Δt内推重比需知道该时间段内的翼载荷。按照可用过载大于需用过载的要求，得到p为

(7)

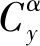
2.2.4 弹道方程

前面已经计算了助推发动机的燃料相对质量因数，为了获得续航发动机燃料相对质量因数，需根据导弹射程Dr，计算所需的续航发动机燃料质量。考虑初步设计时，事先难以确定导弹质量、发动机推力和弹翼面积，故而无法求解微分方程，为此引进相对量参数μ，它表示主级导弹在t时刻所消耗的燃料相对质量因数：

(8)

(9)

式中：Cy为升力系数；x、y分别为发射系x轴、y轴方向的位移。针对本文存在无动力滑翔段，可先通过滑翔高度H、滑翔段弹道倾角θg计算出滑翔距离Dg，然后根据总射程Dr获得有动力飞行的距离Dp，再将Dp作为(9)式积分终点进行求解，最终可得到续航发动机燃料相对质量因数μs.

2.2.5 质量评估

导弹起飞质量mt由助推器质量mb0和主级导弹质量mm组成：

mt=mb0+mm，

(10)

由于本方案助推发动机不与主级导弹不分离，因此mb0=mb. 经过推导，可得到mm的表达式为

(11)

式中：载荷质量mp包括战斗部、弹上制导部件、电气及直属部件、电池等；K1和K2分别为

(12)

Ks为导弹结构相对质量因数(包括弹身与翼面结构质量因数，具体计算见参考文献[18])，αen为发动机结构质量因数(为发动机的结构质量与燃料质量之比，αen一般比较稳定，统计值在0.6～0.7之间)。

由(4)式、(10)式和(11)式可确定导弹起飞质量：

(13)

2.3 代理模型技术

本文构建代理模型的流程为：

1) 利用拉丁超立方抽样(LHS)[19]试验设计方法对由表1和载荷质量及静稳定度组成的9维度设计空间进行抽样，生成200个初始样本点和60个测试样本点；

2) 生成的样本点，利用导弹总体设计模型对样本点进行精确分析，得到导弹质量与约束；

3) 将获得的这一组输入/输出，利用Kriging模型创建代理模型。Kriging模型[20]表示为

g(u)=f(u)+z(u)，

(14)

式中：g(u)为未知Kriging模型；f(u)为已知的关于u的全局近似函数，此处选用0阶模型(f(u)为常数β)；z(u)是均值为0、方差为σ2的随机过程。与样本点有关的协方差为

Cov(z(u(i),z(u(j)))=σ2R[R(u(i),u(j))]，

(15)

式中：R为相关矩阵；R为相关函数，本文选用高斯函数；i=1,2,…,ns;j=1,2,…,ns；ns为样本点个数。相关矩阵R对称正定。高斯函数表达式为

(16)

式中：θ为未知的相关参数；Nv为设计变量维度，本文Nv=7. 未知点u处的预测值(u)的表达式为

(u)=+rT(u)R-1(g-f)，

(17)

式中：g为长度为ns的列向量，为样本点的真实响应值；f是一个长度为ns的单位列向量；rT(u)为未知点u和样本数据之间的相关向量，其表达式为

rT(u)=[R(u,u1)R(u,u2) …R(u,uns)]T;

(18)

=(fTR-1f)-1fTR-1g.

(19)

方差估计值的表达式为

(20)

(16)式中的相关参数θ可由最大似然估计给出：

(21)

(22)

式中：N为测试样本点个数；qsi和si分别为第i个测试样本点所对应的精确值和响应值；σe代表了所有样本点相对误差在周围的集中程度；和σe的值越接近0，表示代理模型精度越高。

5) 如果定义的上述两个统计量均小于5%，那么代理模型构建完毕，否则返回第1步，增加50个样本点更新Kriging模型，直至满足收敛标准。

通过2次迭代，当样本量达到300时，构建的代理模型可满足拟合精度要求，如表4所示。由于计算中发现仅有ve与AR为有效约束，此处仅给出了ve与AR的代理模型。Kriging构建关于导弹质量、末速与展弦比的代理模型关于60个测试样本点的预测结果如图7所示。

表4 代理模型拟合精度Tab.4 Fitting precision of surrogate model

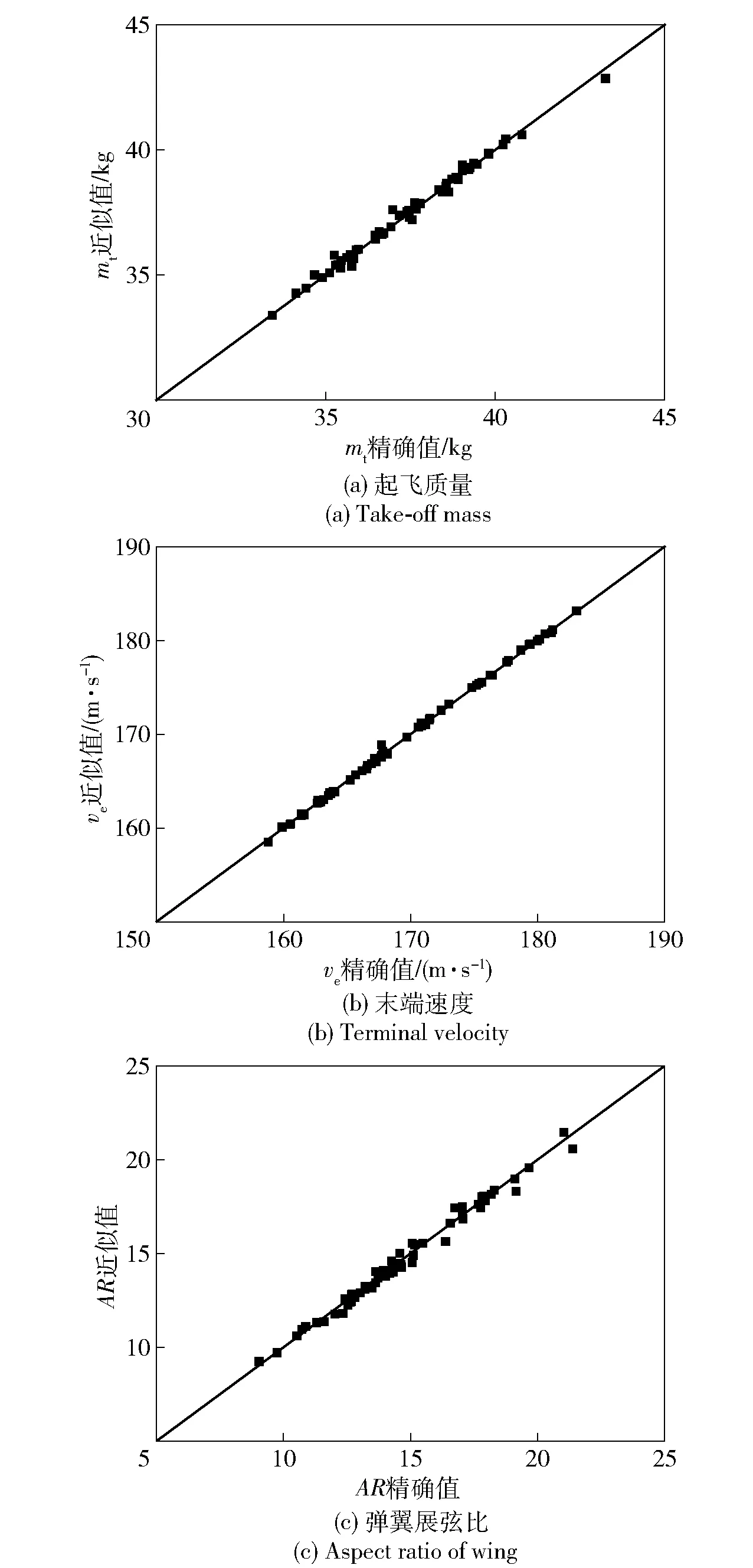
图7 代理模型样本点测试Fig.7 Sample points of surrogate model

3 结果与分析

为了对比，利用确定性优化算法，设计了质量最小的导弹。下面分别针对3类不确定性问题，将稳健性与确定性优化设计结果进行讨论与分析。

3.1 载荷质量与质心位置不确定性

图8给出了载荷质量与质心位置不确定时，稳健性优化得到的导弹质量Pareto前沿，同时列出了确定性优化最佳设计点P0的不确定性分析结果。由图8可知，P0的质量标准差高达1.86 kg，说明此类导弹对质量与质心位置变化非常敏感。为了探究载荷质量与质心位置变化对导弹起飞质量与约束的影响，从 Pareto前沿中选取了3个典型的设计点P1、P2和P3进行分析，对应得到的相关参数如表5所示。通过对比，存在如下特点：

1) 从P0到P3质量方差σmt逐渐降低。根据(13)式，如果燃料质量系数越小，mp变化引起的mt变化则越小。而在射程给定的条件下，导弹滑翔距离越大，有动力飞行距离就越小，可降低燃料质量系数。因此，为了降低σmt，需要增加滑翔距离。飞行动力学表明：导弹飞行高度H越高，无动力滑翔初速vs与末速ve之比越大、阻力系数越小，滑翔距离就越远。由表4稳健性优化结果可知，设计点P3的飞行高度最高、vs最大，从而使其σmt最低。但是，增加vs会使续航段推重比增加，导致全弹质量变大，即μmt从P0到P3逐渐增加。

图8 载荷质量与质心位置不确定时的稳健性优化Pareto前沿Fig.8 Pareto front of RDO under payload weight and center-of-mass location uncertainty

表5 载荷质量与质心位置不确定时的稳健性优化设计结果

Tab.5 Results of RDO under payload weight and center-of-mass location uncertainty

输出参数P0P1P2P3vb/(m·s-1)178.8182.3194.9199.9vs/(m·s-1)164.6165.5167.7170.2H/m143.2149.8160.1184.4设计θc/(°)8.927.397.317.64变量θg/(°)-15.0-15.0-15.0-15.0bw/m0.9220.9100.8780.862bf/m0.3650.3780.3810.390质量μmt/kg34.5234.6134.9535.59σmt/kg1.8611.6951.5921.532约束P{ve≥160m/s}/%33.8990.0494.0093.51P{AR≤12}/%31.32100.00100.00100.00

3) 载荷质量不确定性使得AR满足概率的约束大幅度降低。由于载荷质量会减小，在设计时所需要的弹翼面积同步减小，使得展弦比增大，增加了展弦比进一步增大Cymax，从而提高翼载荷。根据(2)式，pm越大，弹翼面积就越小，迭代中这就使得AR越来越大，最终不满足设计约束。根据优化结果，为了提升AR满足约束的概率，需要降低bw. 需要注意的是，减小弹翼展长会使展弦比降低，从而降低奥斯瓦尔效率因子，增大诱导阻力，导致全弹起飞质量变大。

4) 由(5)式可知，增加助推末速vb使助推段燃料增大；由(6)式可知，增加vb可降低dv/dt，进而减小续航段推重比实现续航段燃料质量的降低。因此，从mt最小的角度来看，助推发动机与续航发动机对vb的要求是矛盾的。由表4中的Pareto最优设计结果可以看出，随着vs的增加，一定程度增加vb可带来更小的mt.

5) 通过上述分析，在载荷质量与质心位置不确定条件下，为增加质量稳健性与约束稳健性而采取的设计方法，必然会引起导弹起飞质量的增加。图7所示的稳健性优化各设计点的μmt均要高于P0点，并且随着σmt的减小，μmt逐渐增大。总得来说，ParetoP2设计方案能较好地兼顾均值和方差，与P0相比，σmt降低了19.8%，μmt增加了1.20%.

3.2 速度方案不确定性

速度方案vb和vs分别影响助推发动机质量与续航发动机推重比，它们直接关系着导弹的起飞质量。减小vs可以降低续航段推重比，从而减小续航发动机质量，但同时会降低导弹末速ve，减小滑翔距离，影响导弹质量稳健性。因此，当速度方案不确定时，需合理匹配其余总体参数，才能在性能和约束之间做出较好的折衷。

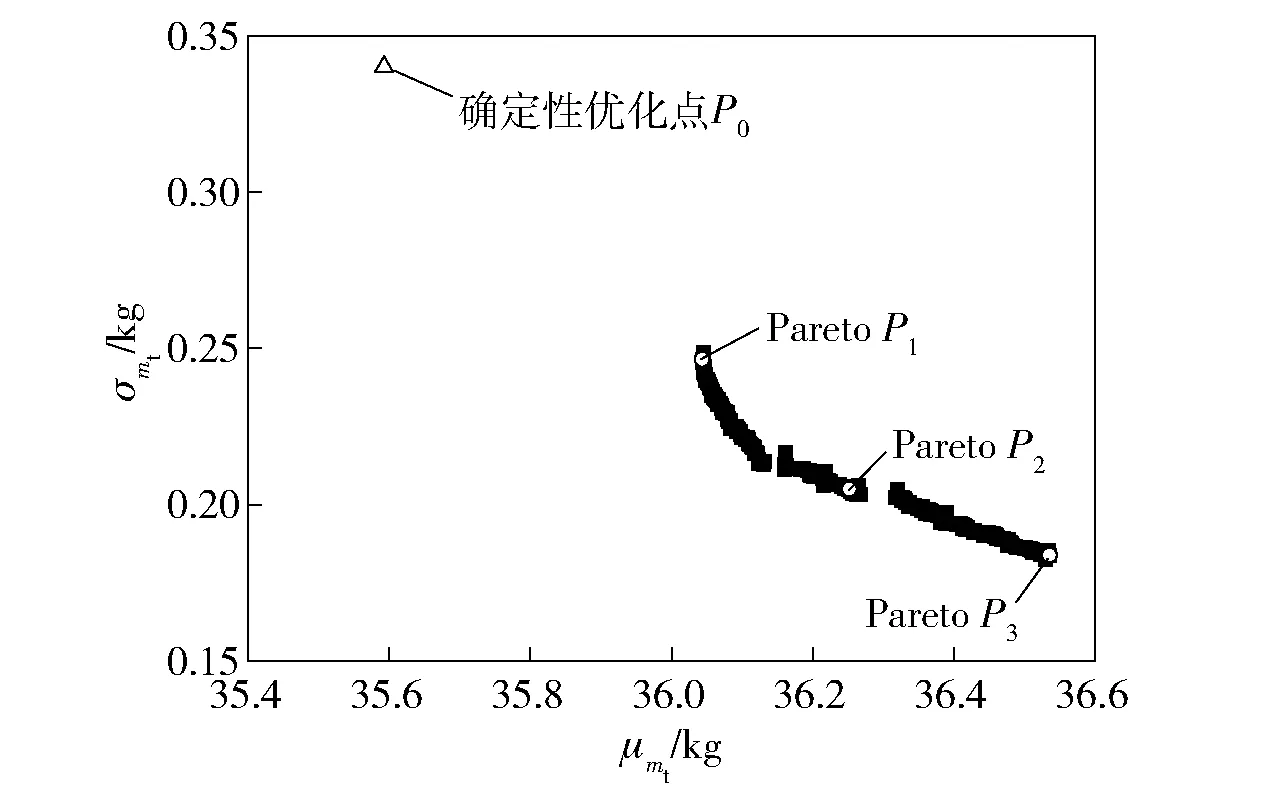
图9 飞行速度不确定时的稳健性优化Pareto前沿Fig.9 Pareto front of RDO under velocity uncertainty

图9给出了速度方案不确定时，稳健性优化得到的导弹质量Pareto前沿解集，同时列出了确定性优化最佳设计点P0的不确定性分析结果。从图9可知，飞行速度不确定性引起的全弹σmt(约0.34 kg)要明显低于载荷质量与质心位置变化引起的全弹σmt(约1.86 kg)。类似地，从Pareto前沿中选取了3个典型的点P1、P2和P3进行分析，对应得到的相关参数如表6所示。

表6 速度方案不确定时的稳健性优化设计结果Tab.6 Results of RDO under velocity uncertainty

优化结果表明：与载荷质量和质心位置不确定影响类似，为降低导弹σmt，需增加飞行高度H与滑翔段初速vs；为满足末速约束概率，需提升vs；为满足展弦比约束概率，需减小bw；而增加飞行高度H、vs，减小bw均会导致μmt增加。相比于确定性设计方案P0，P2的质量均值增加了1.90%，标准差降低了43%，满足末速约束从49.79%提升至90.74%，满足展弦比约束从58.37%提升至100%.

3.3 弹道方案不确定性

图10 弹道方案不确定时的稳健性优化Pareto前沿Fig.10 Pareto front of RDO under trajectory uncertainty

图10显示了弹道方案不确定时，稳健性优化得到的质量Pareto前沿。由图10可知，弹道方案不确定时，确定性优化设计点P0的σmt仅为0.07 kg，远远低于前文其他因素不确定性造成的质量波动。因此，在总体设计阶段，此类导弹弹道方案在设计状态小范围浮动不会对其起飞质量产生显著影响。

尽管弹道方案不确定性对导弹质量影响较小，但飞行高度与俯冲段弹道倾角均会影响无动力滑翔阶段的末速，进而影响导弹翼载荷，使满足约束的概率降低。因此在表7中，为了增加满足末速约束的概率需要提高vs，为了满足展弦比约束的概率需要降低bw.

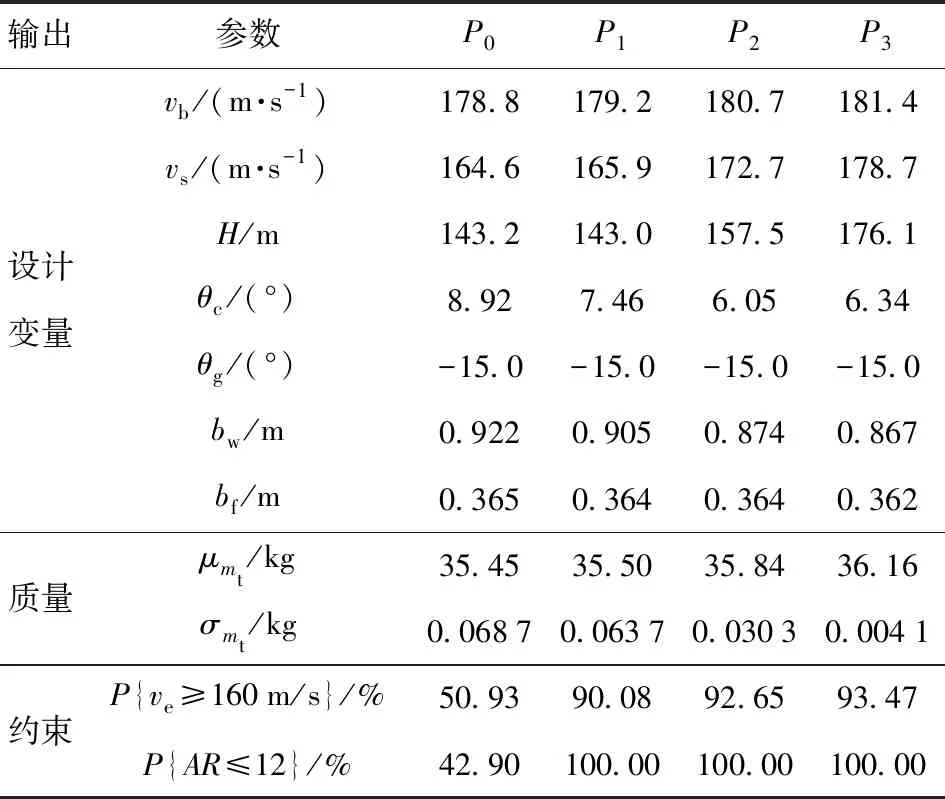
表7 弹道方案不确定时的稳健性优化设计结果Tab.7 Results of RDO under trajectory uncertainty

4 结论

1) 针对模块化导弹设计中存在的多种不确定性因素，本文以导弹起飞质量为目标，提出一种模块化直升机载空地导弹稳健性优化设计方法。优化结果表明：相比于传统确定性优化，稳健性优化在付出很小质量代价基础上，可降低不确定性因素对设计目标的影响，大幅度提升满足设计约束的概率。

2) 通过对工程研制过程中常见的3类不确定性问题分析，结果表明：载荷质量与质心位置变化对模块化直升机载空地导弹的起飞质量影响最大，其次是速度方案变化，而弹道方案不确定性对此类导弹起飞质量几乎没有影响。

3) 模块化直升机载空地导弹起飞质量与约束稳健性设计准则：增加导弹飞行高度与提升续航阶段末速可降低不确定性变量对模块化直升机载空地导弹起飞质量的影响；一定程度上增加助推段末速能降低导弹起飞质量；增加续航段末速、减小弹翼展长与增加尾舵展长提升了满足约束的概率。

4) 本文构建的模块化战术导弹稳健性优化设计框架，还可用于研究弹翼、尾舵、发动机等部件模块化产生的不确定性对导弹设计的影响，提高全构型模块化战术导弹设计稳健性。