JO-9C小尺寸传爆药驱动飞片影响因素模拟仿真研究
2020-03-05刘荣强聂建新焦清介徐新春
刘荣强, 聂建新, 焦清介, 徐新春
(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081;2.北京动力机械研究所, 北京 100074)
0 引言
在航天器和武器系统的传爆序列中,当施主装药与受主装药之间存在较大的空气隙界面时,仅依靠施主装药爆轰直接输出冲击波和爆轰产物不能可靠引爆受主装药;然而,在施主装药底部增加一定厚度的金属片(即飞片),可显著提高受主装药起爆的可靠性[1]。飞片传爆原理是飞片吸收炸药爆轰能量后转变为动能,撞击受主装药后产生较高的冲击波压力,进而实现可靠传爆。Prinse等[2]采用冲击片雷管驱动飞片实现了钝感传爆药的可靠传爆,研究表明采用冲击片雷管能够大幅度提高其传爆能力。Toon[3]、Dean等[4]和Trott等[5]的研究也验证了飞片传爆的优势。由于飞片传爆具有较长的可靠传播距离、较高的安全性和较强的恶劣环境适应能力[6-8],广泛应用于各武器系统的传爆序列中,尤其对战斗部小型化具有重要意义。
飞片传爆结构的材料和尺寸参数对飞片速度和形貌影响很大。谭迎新等[7]研究了不同加速膛材料对飞片速度的影响,结果表明蓝宝石具有良好的加工性能,加速膛口部规则、锋利,最适合用作加速膛材料;蒋小华等[9]采用VLW状态方程计算了不同密度季戊四醇四硝酸酯(PETN)的JWL状态参数,利用仿真软件LS-DYNA模拟计算出飞片速度,其结果与试验结果基本吻合,验证了数值模拟计算飞片速度的可行性,并得到了飞片速度与炸药密度的关系;程松[10]采用电磁法测试技术测量直径为1.5~5.0 mm小尺寸装药爆轰驱动下的飞片速度,获得了装药直径、飞片厚度及加速膛长度与飞片速度的关系;简国祚等[11]、郭俊峰等[12]研究了叠氮化铜装药驱动飞片的作用过程及不同飞片材料下的形貌;陈清畴等[13]采用数值模拟方法计算获得了六硝基茋炸药驱动不同材料、不同厚度和不同直径飞片速度与形态。然而,现有工作大多采用试验或仿真方法研究单一因素对飞片效能的影响规律,无法整体把握飞片传爆结构参数与飞片效能的关联关系。
数值仿真对于飞片传爆结构的优化设计有重要指导作用,用于驱动飞片的装药结构爆轰产物状态方程是仿真准确与否的关键。JO-9C装药是典型的HMX基传爆药,具有较高的可靠性和安全性,广泛应用于传爆序列中。徐新春等[14]、张少明等[15]对小直径JO-9C的爆轰机理进行了大量试验及理论研究;袁俊明等[16]对装有JO-9C的传爆管殉爆过程进行了仿真研究;Li等[17]对JO-11C的点火增长模型进行了标定,建立仿真模型计算了小尺寸下JO-11C的爆速、爆压随直径的变化规律,与试验数据吻合较好。
上述研究中JO系列装药的JWL状态方程参数采用了配方类似的LX-10和PBX-9501代替,由于国内外装药条件及装药密度的区别,直接用LX-10和PBX-9501的JWL状态方程参数替换,显然是不够准确的。传爆药爆轰产物JWL状态方程参数的标定方法也鲜有报道。
综上所述,本文围绕飞片传爆的结构设计和性能优化问题,建立了小尺寸传爆药驱动飞片作动的仿真模型,以典型传爆药JO-9C为例,提出了一种获取传爆药爆轰产物JWL状态方程参数的计算方法,并基于仿真模型计算获得了飞片传爆结构参数与飞片效能的关联关系,本研究可为飞片传爆序列的结构优化设计提供理论指导。
1 传爆药驱动飞片仿真建模
1.1 作用原理
传爆药驱动飞片的典型结构主要包括传爆药、壳体、飞片和加速膛4部分(如图1所示)。根据具体使用环境,壳体可选择金属或有机玻璃等非金属材料,飞片可选择金属或非金属材料,加速膛内壁要对飞片起到剪切作用,一般选取硬度较高的蓝宝石或陶瓷材料。传爆药驱动飞片通常作为传爆序列的首发能源,其作用原理为:传爆药被引爆后,装药内部形成爆轰波,在装药结构与飞片的界面上衰减为冲击波,飞片在冲击波和爆轰产物的共同作用下发生剪切成形,在加速膛内加速飞行,最终飞片以相对稳定的速度冲击下级装药,从而实现传爆序列能量的传递过程。
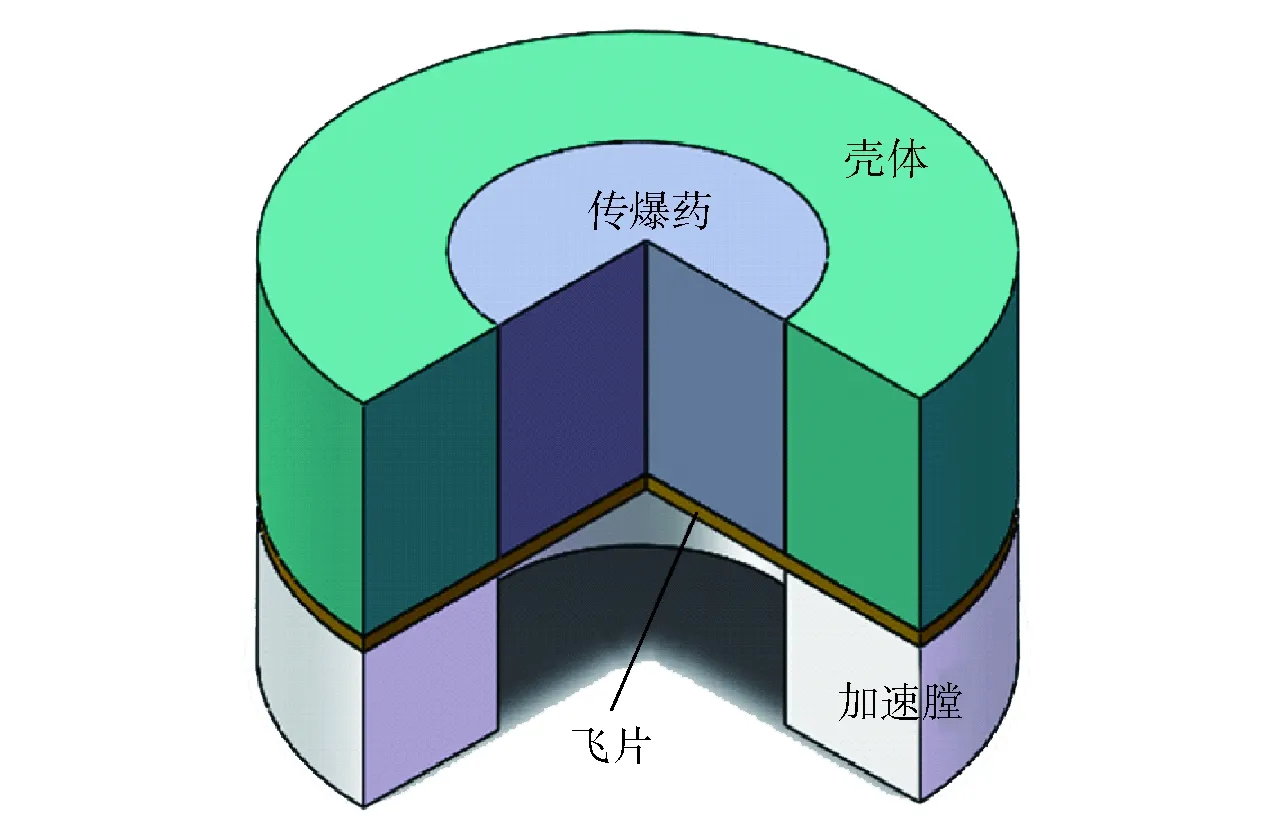
图1 传爆药驱动飞片典型结构Fig.1 Typical structure of flyer driven by booster explosive
1.2 仿真模型
本文应用AUTODYN软件,建立典型传爆药装药驱动飞片的二维轴对称模型,采用流固耦合算法,装药和空气域为欧拉单元,飞片、壳体及加速膛为拉格朗日单元。在欧拉网格边界处设置流出边界条件,模拟无限大空气域。一般的,外壳为金属或高分子材料,飞片为金属材料,加速膛为蓝宝石等脆性材料。各部件的材料模型及参数如下:
欧拉网格中填充的空气用理想气体状态方程描述为
pa=(γ-1)ρaEg,
(1)
式中:pa为空气压力;γ是绝热指数,对于理想气体有γ=1.4;ρa是空气密度,其初始密度为0.001 225 g/cm3;初始压力为一个标准大气压;Eg=2.068×10-5,是气体比内能。
飞片在冲击波及爆轰产物的共同作用下发生剪切成形时,飞片材料表现出大变形、高应变率和高温等特征。为准确描述飞片在此状态下的响应规律,采用Johnson-Cook模型来描述。Johnson-Cook模型常用于模拟金属材料从低应变率到高应变率下的动态行为,该模型采用变量乘积关系描述了应变率、温度和应变的影响,本构方程为
(2)
式中:σvp为von Mises流动应力;εvp为黏塑性应变;Ays为屈服强度;Bhc为材料塑性硬化系数;Che为黏塑性硬化指数;n为应变率敏感指数;ε′vp为真实黏塑性应变率;ε′0为参考应变率;m为温度软化指数;T*为无量纲温度,T*计算公式为
T*=(T-Tr)/(Tm-Tr),
(3)
Tm为材料的熔点温度,Tr为参考温度(一般取为实验时室温),T为温度,温度单位采用国际制单位。
传爆药的外壳通常为金属或高分子材料,可采用弹塑性模型和Gruneisen状态方程描述其动态行为。加速膛一般采用蓝宝石材料,可采用shock状态方程和von Mises强度方程描述其动态行为。
1.3 传爆药状态方程参数计算方法
JWL状态方程是典型的动力学状态方程,是一种不显含化学反应、由实验方法确定参数的经验状态方程,能比较精确地描述爆轰产物的膨胀驱动做功过程。炸药爆轰产物JWL状态方程的标准形式为
(4)
式中:p为爆轰产物的压力(Pa);V为爆轰产物的相对比容,V=v/v0,为无量纲量,v=1/ρd为爆轰产物的比容,ρd为爆轰产物的密度,v0为爆轰前炸药的初始比容;e0为比内能(J/m3);A、B、R1、R2、ω为常数。
炸药的JWL状态方程参数一般采用标准圆筒试验的方法进行标定,其试验成本较高、周期长,且只能获得装药在某种特定状态下的JWL状态方程参数。本文提出了一种获取传爆药爆轰产物JWL状态方程参数的计算方法,即:基于BKW方程及爆轰静态模型的化学平衡,应用Explo-5软件求解反应产物之间的热力学方程,确定平衡状态下的系统组成,从而计算得到爆速、爆压和爆热等参数,并拟合得到爆轰产物JWL状态方程参数。
(5)
式中:R为气体常数;xi是第i种产物在总的爆炸产物中所占的摩尔数,i=1,2,3,…;ki是第i种爆炸产物的余容因数;α、β、k和θ为经验常数。
典型传爆药JO-9C由95%奥克托今(HMX)和5%氟橡胶组成,压装密度为1.707 g/cm3,应用Explo-5软件计算得到其爆轰参数及爆轰产物JWL状态方程参数如表1所示。

表1 JO-9C传爆药的JWL参数Tab.1 JWL parameters of JO-9C booster explosive
注:ρ0为炸药压装密度,D为炸药爆速。
1.4 驱动飞片模拟及速度分析
本文建立了JO-9C传爆药驱动飞片的仿真模型(如图2(a)所示),模拟飞片剪切成形及加速飞行的过程细节,分析飞片在加速膛中的运动规律。装药尺寸为φ5 mm×38 mm,装药外壳的外径为φ20 mm,飞片厚度为0.5 mm,加速膛内径为φ5 mm,外径为φ20 mm,长度为5 mm,空气域尺寸为60 mm×20 mm,网格尺寸为0.1 mm×0.1 mm. 沿飞片径向设置6个监测点(如图2(b)),监测飞片的飞行速度随时间的变化关系,并在装药左侧中心处设置起爆点,采用毫米- 毫克- 毫秒单位制。
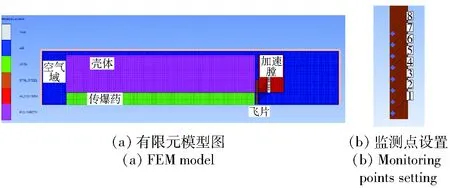
图2 JO-9C装药驱动飞片仿真模型Fig.2 Simulation model of flyer driven by JO-9C
不锈钢飞片的Johnson-Cook模型参数如表2所示,有机玻璃外壳的材料参数如表3所示。蓝宝石加速膛的密度为3.9 g/cm3,剪切模量为100 GPa,屈服强度为8 GPa.

表2 不锈钢的Johnson-Cook模型参数Tab.2 Johnson-Cook model parameters of stainless steel
注:ε为应变。
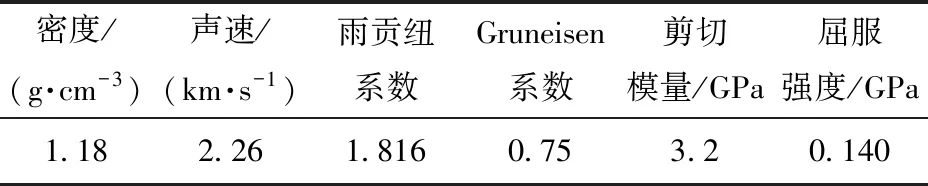
表3 有机玻璃的材料参数Tab.3 Material parameters of PMMA
结果表明,飞片的生成和发展存在一个弯曲变形、剪切成形和加速运动的过程(如图3所示)。JO-9C装药起爆后,爆轰波沿装药向右传播,飞片在冲击波及爆轰产物压力作用下,开始向右加速;在加速膛的强约束作用下,飞片开始发生剪切变形;随着飞片继续向右运动,飞片与加速膛接触位置变形加剧,并最终超过飞片材料的强度极限,发生破坏断裂;此后,飞片在加速膛内继续加速运动,并最终达到一个稳定速度。
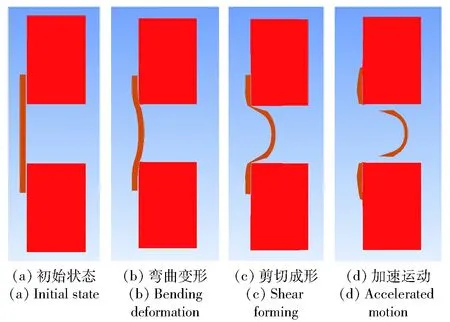
图3 飞片剪切成形并加速运动过程Fig.3 Process of flyer shear forming and accelration
为分析飞片在加速膛运动过程中的速度变化规律,本文提取了飞片沿径向各监测点位置处的速度时程曲线(如图4所示)。计算结果表明,飞片速度沿径向存在速度梯度,中心位置速度最大,沿径向速度不断减小。在冲击波及爆轰产物驱动下,飞片不断加速,如图4中监测点6所示,由于其靠近飞片与加速膛边界处,需克服材料的剪切破坏,导致该位置处速度较低,但在飞片断裂后,这种阻碍作用消失,由于速度梯度的原因,促使该位置处的速度继续增大,最终趋于稳定值,约1 377 m/s. 同理,在飞片中心位置处(监测点1曲线),剪切应力的影响不明显,其初始加速度更大,很快达到最大速度1 800 m/s,在飞片断裂后,由于速度梯度的存在,拉动外侧飞片加速,故中心位置处的速度不断减小,并最终趋于稳定值,由此也导致飞片呈球面状。

图4 飞片沿径向监测点位置处的速度时程曲线Fig.4 Velocities of flyer at different monitoring points
2 传爆药驱动飞片仿真模型的试验验证
2.1 试验测试系统及试验件配置
为验证所建立的传爆药驱动飞片仿真模型准确性,本文设计了JO-9C传爆药驱动飞片试验,应用电磁法测试飞片速度,爆轰驱动飞片试验测试系统原理图如图5所示,试验测试系统现场布置图如图6所示。试验前,用胶水将装药内孔、飞片、蓝宝石加速膛内孔和电磁速度传感器闭合回路的端面对正粘合,以保证装药爆轰时可以驱动飞片沿蓝宝石加速膛的内孔圆周顺利剪切成型。试验件配置参数与本文1.4节中仿真模型一致。
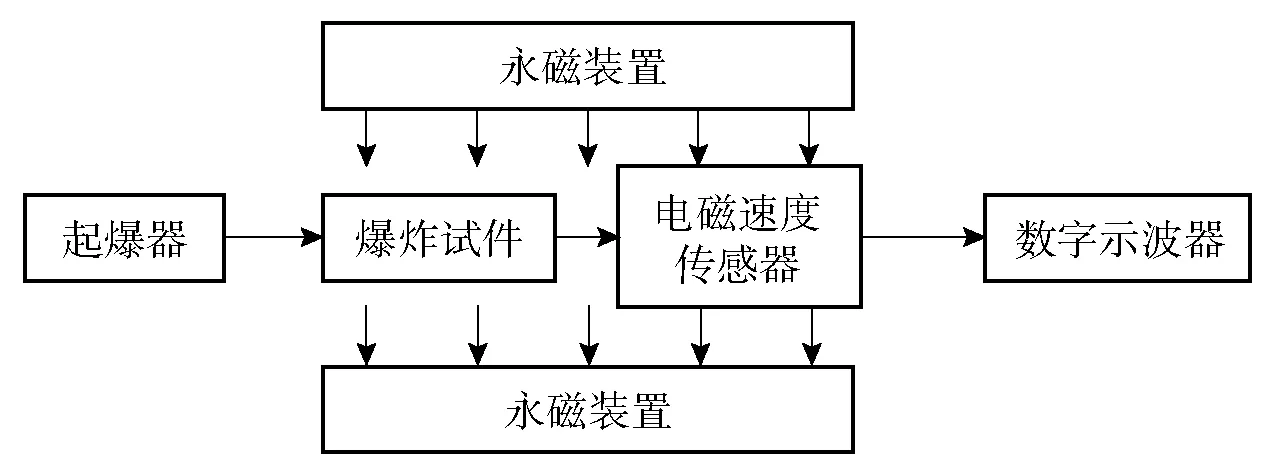
图5 电磁法测试飞片速度测试系统原理示意图Fig.5 Schematic diagram of flyer speed measurement system based on electromagnetic method

图6 爆轰驱动飞片试验测试系统Fig.6 Test system of flyer driven by detonation
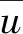
(6)
2.2 计算值与试验值对比
对数值模拟中得到的飞片速度时程曲线对时间积分,可得到不同监测点处的位移时程曲线,从而对比得出飞片运动到0.2 mm、0.5 mm、1.0 mm、1.5 mm、2.5 mm位置处的时间,再对应速度时程曲线,提取出该位移下的速度,如表4所示。

表4 不同监测点的位移- 速度对应关系Tab.4 Relationship between displacement and velocity at different monitoring points
由监测点1~7的数据可知:飞片在1.0 mm位移内便达到最大速度;在1.0~2.0 mm位移内,速度略有降低。由于表4中的数据为飞片在不同位移下的瞬时速度,而表5中的速度为不同位移内的平均速度,所以表4中的数据大于表5中的数据。为更好地对比仿真结果与试验结果,计算出仿真中不同位移内的平均速度。由于飞片在剪切飞行过程中并非平面,首先切割磁场与撞击速度传感器为飞片中心位置,故以监测点1处得到的位移时程曲线计算不同位移内的平均速度。
将飞片速度的计算结果与试验值进行对比。由表5可知,仿真计算得到的不同位移内飞片的平均速度与试验数据相比,最大误差为10.69%,验证了本文提出仿真模型的有效性。
图7为飞片速度在不同位移下的变化曲线,试验只测得了一段位移内的平均速度,所以飞片速度测试值随位移增大而增大。而图7中的仿真结果表明,对该试验件配置而言,飞片在0.5 mm内已完成加速过程,其运动速度达到最大值,在后面的1.0~2.0 mm位移内速度几乎保持不变。通过仿真计算,可加深对爆轰驱动飞片运动整个过程的认知,展现试验中所无法观测到的细节现象。
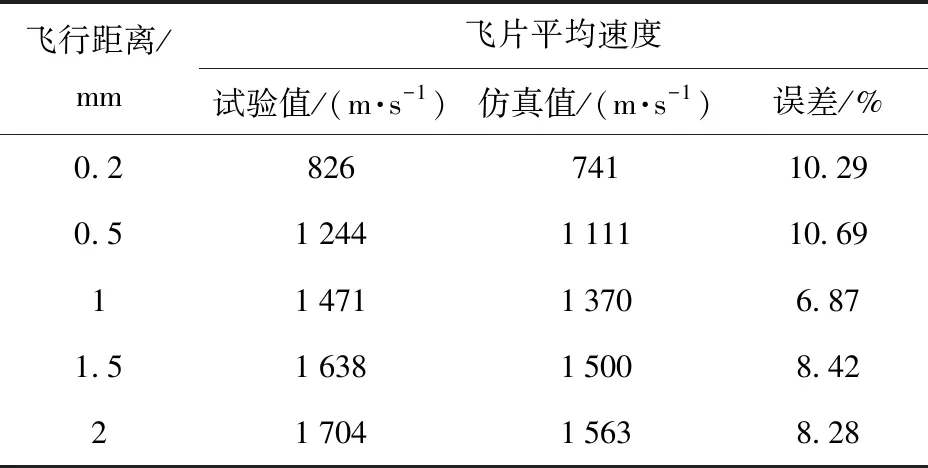
表5 飞片速度的仿真值与试验值对比Tab.5 Simulated and experimental results of flyer velocity
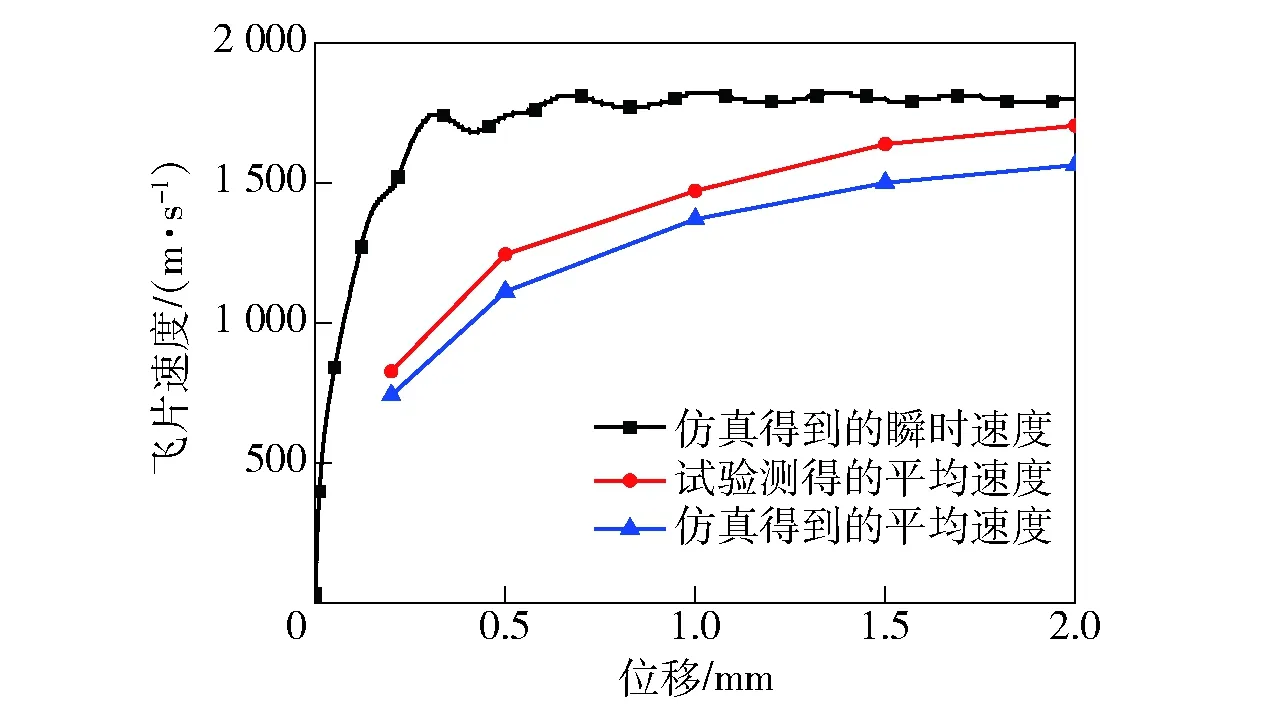
图7 不同位移下的飞片速度对比Fig.7 Flyer velocities under different displacements
3 传爆药驱动飞片作用效能影响因素分析
在传爆序列飞片起爆理论中,飞片经空气隙撞击到下级装药上,下级装药是否起爆主要取决于其受到的冲击能量,而这一能量与压力、脉冲宽度有关。起爆能量决定了下一级装药能否形成热点并成长为爆轰,当起爆能量小于某一值时,热点不能形成。因此,传爆药驱动飞片过程中,应充分考虑飞片的速度与动能。基于以上仿真模型及材料模型参数,仿真分析装药尺寸、飞片厚度、加速膛直径3个方面对飞片速度及动能的影响规律。
3.1 装药结构
设计驱动飞片的数值仿真模型,装药直径d为3 mm、5 mm、8 mm,装药长度为0.5d、d、1.5d、2d、4d,研究飞片速度及动能与装药结构之间的关系,如图8所示。由图8可知:对于3种不同直径装药,飞片速度及动能均随装药长度增大而增大,但逐渐趋于平缓;当装药长度为1.5d时,飞片速度及动能达到一个较高值;继续增大装药长度,飞片速度及动能增长较小;考虑到装药安全性及空间等,1.5d为较佳的设计装药长度。其中,飞片速度的获取方法与1.4节相同,飞片动能在仿真软件中根据飞片材料的动能提取。
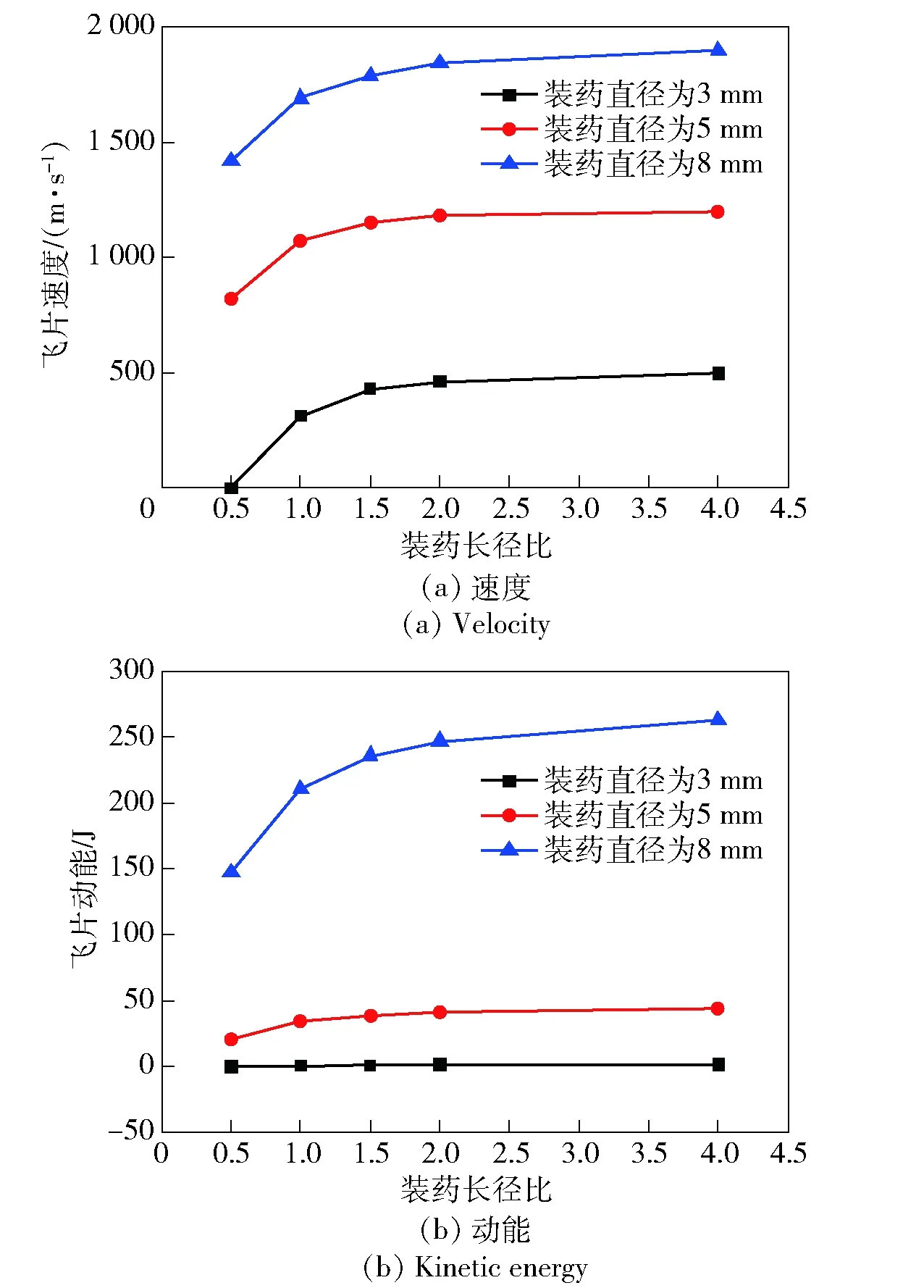
图8 飞片速度及动能随装药长径比的变化关系Fig.8 Changes of flyer velocity and kinetic energy with length-to-diameter ratio of booster explosive
3.2 加速膛直径
保持长径比为1.5,装药直径为5 mm,飞片厚度为0.5 mm,加速膛直径分别为3 mm、4 mm、5 mm、6 mm、8 mm,建立驱动飞片的数值模型,研究加速膛直径对飞片速度、动能及形貌的影响规律,如图9所示。由图9可以看出:随加速膛直径增大,飞片速度降低;当加速膛直径为8 mm时,飞片速度反而略有增大,这是因为飞片在飞行过程中发生断裂,周边部分材料脱落,导致中心位置处的飞片速度略大(如图10所示)。随加速膛直径增大,飞片动能逐渐增大,但由于直径过大会导致飞片断裂,实际对外做功的部分飞片动能并不大。
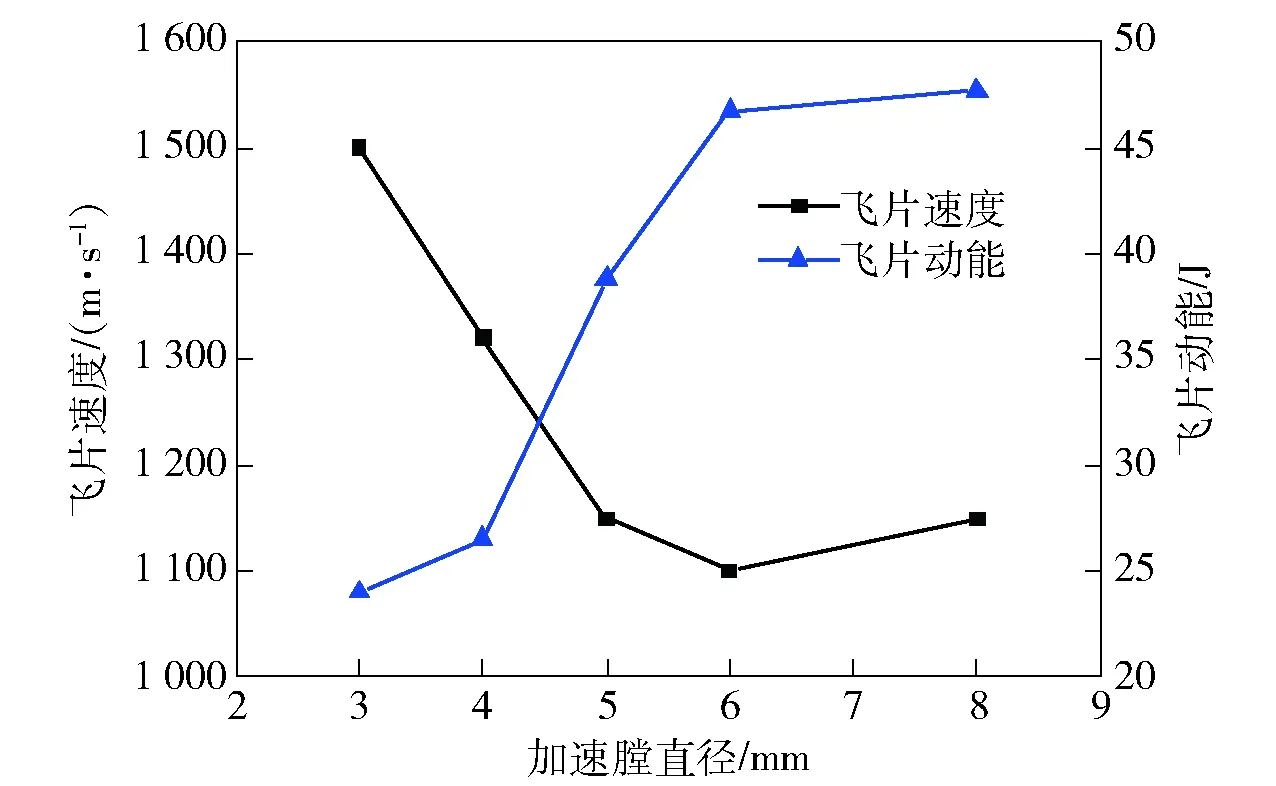
图9 不同加速膛直径下飞片的速度与动能对比Fig.9 Flyer velocity and kinetic energy with different diameters of accelerating chambers
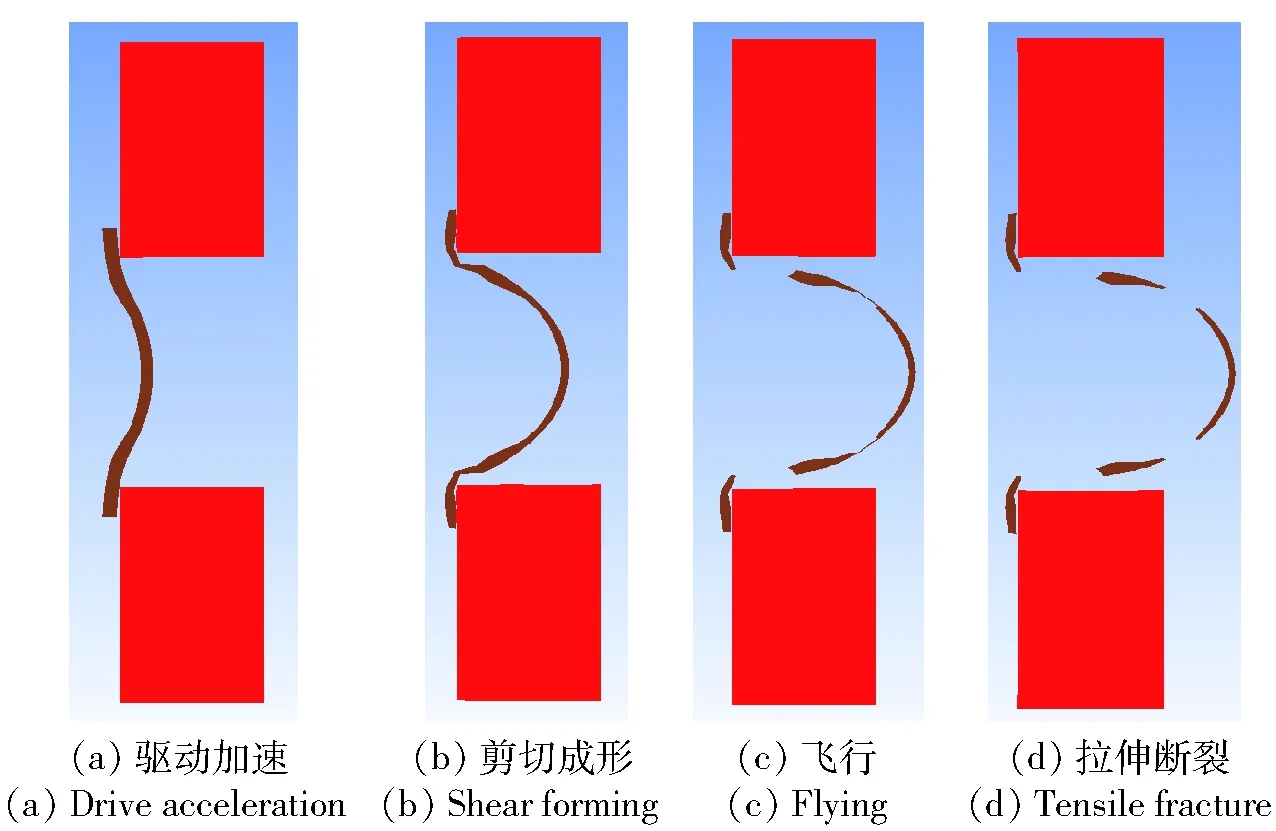
图10 大直径加速膛下飞片成形及加速过程Fig.10 Process of flyer shear forming and accelration in accelerating chamber with large diameter
加速膛直径小于等于装药直径时,飞片剪切成形并加速的运动过程与图2基本一致;而当加速膛直径大于装药直径时,飞片中心位置首先在冲击波及爆轰产物作用下发生加速,由于加速膛直径较大,飞片外侧并没有受到爆轰产物的直接驱动,而是在飞片中心部分的拉力作用下向前运动,这也导致飞片沿径向拉伸严重,当飞片向前运动到加速膛边界处时,开始发生剪切变形,最终断裂在加速膛中飞行。在速度梯度导致的拉伸应力下,飞片继续拉伸变薄,并最终发生破坏。
因此,在装药结构一定情况下,加速膛直径应不大于装药直径,考虑到能量利用率等,加速膛直径也不应过小,与装药直径相当为佳。
3.3 飞片厚度
保持长径比为1.5,装药直径为5 mm,加速膛直径与装药直径一致,设计装药驱动0.2 mm、0.3 mm、0.4 mm、0.5 mm、0.6 mm 5种厚度飞片的数值模型,研究飞片速度及动能随飞片厚度的变化关系,如图11所示。由图11可以看出:在装药结构保持不变情况下,飞片速度随厚度的增加而降低,但是飞片厚度的增加便会导致被切割飞片的质量增大,飞片动能与厚度之间并非简单的线性关系,而是存在一个极大值;在本模型中,飞片厚度在0.3 mm时,飞片动能达到极大值。此外,当飞片厚度为0.2 mm时,飞片在飞行过程中发生断裂,如图12所示。这应与飞片内部存在速度梯度,从而产生拉伸应力有关,也说明飞片的飞行距离不可过长,否则容易出现断裂、不稳定等情况。因此,在设计装药驱动飞片时,应根据输出作用需求,综合考虑飞片速度和动能的优先级,以确定合适的飞片厚度。
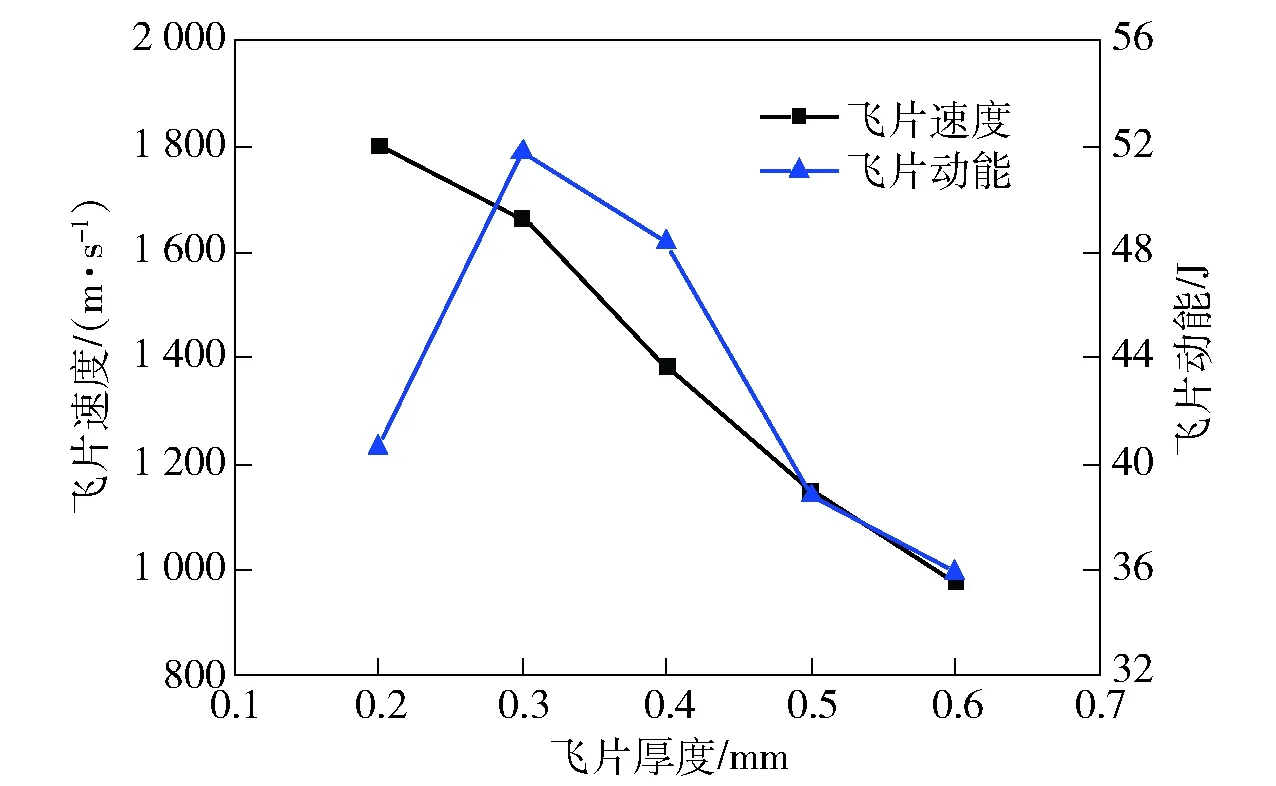
图11 不同飞片厚度下的速度与动能对比Fig.11 Velocity and kinetic energy of flyer with different thickness
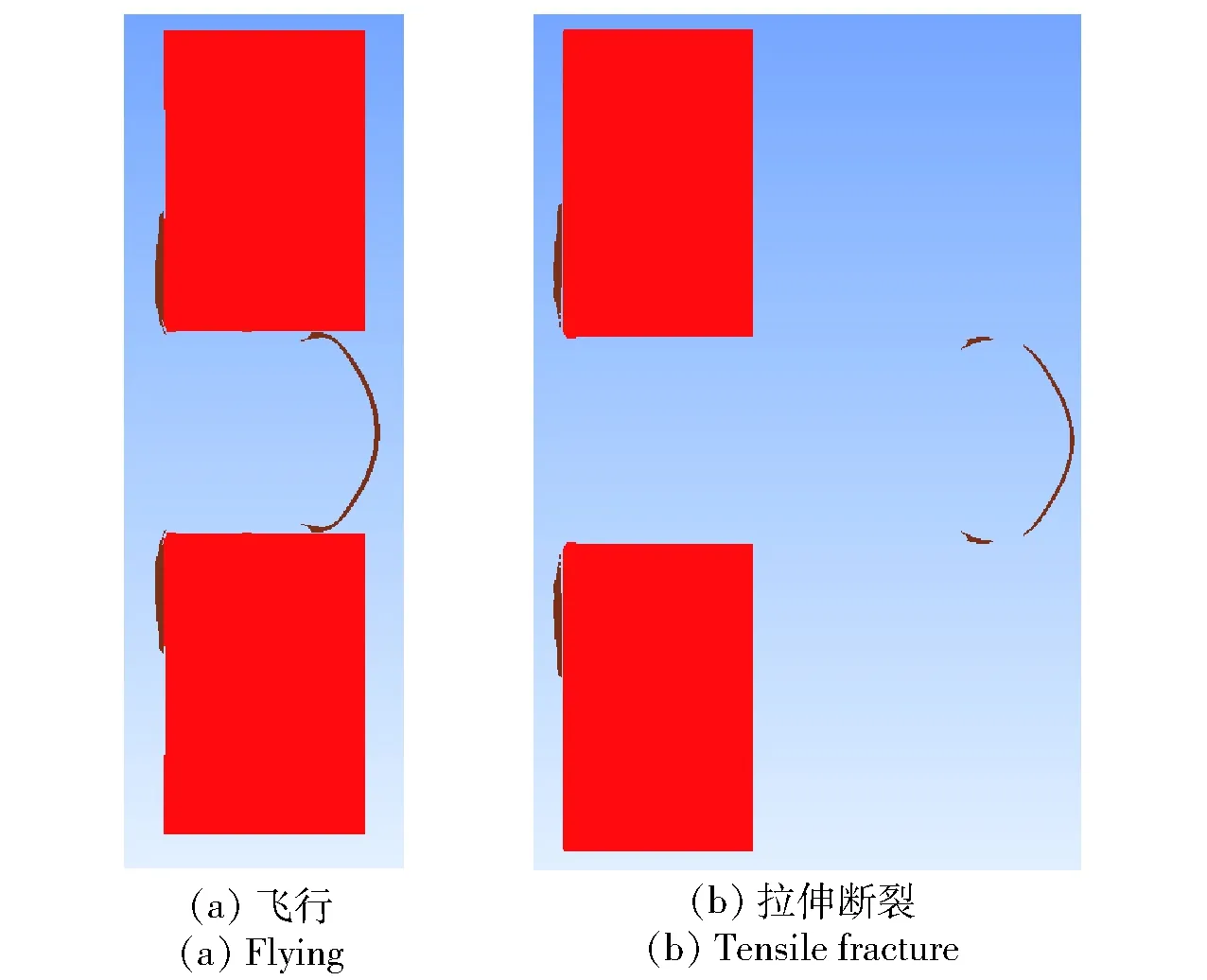
图12 0.2 mm厚的飞片断裂过程Fig.12 Fracture process of 0.2 mm-thick flyer
4 结论
1)飞片内部沿径向的速度梯度是导致飞片发生弯曲变形的主要原因。
2)装药长径比为1.5时,能兼顾飞片速度与装药量,是合适的装药长径比选择。
3)飞片厚度越大,速度越低;飞片过薄时易出现断裂,且飞片动能存在一个极大值,应针对不同结构对飞片厚度进行优化设计。
4)加速膛直径应不大于装药直径,能保证良好的飞片形貌及飞行速度,否则飞片弯曲严重且易发生断裂。
5)5 mm直径JO-9C的最优装药结构设计参数:长径比为1.5,即装药高度为7.5 mm;加速膛直径为5 mm,飞片厚度为0.3 mm,此时飞片速度为1 663 m/s,动能为51.79 J.
