基于球面A·r约束的大地距离解算模型

单玉浩，杨晓东，邢世宏

(海军潜艇学院，山东 青岛 266000)

几何大地测量采用一个同地球外形最为接近的旋转椭球作为参考模型，研究地球椭球数学性质、椭球投影数学变换、椭球面测量计算等。几何大地测量可为航海提供定位、定向、导航信息[1]，也可为目标运动要素解算提供依据。大地主题解算[2]是几何大地测量问题中的一个重要方面，比较经典的方法有直接对大地线微分方程进行积分的方法和利用地图投影理论解算大地问题的方法[3-4]。类似贝塞尔法[5]等一些主题解算方法都是利用地图投影理论，先将椭球面问题对应到球面问题加以解决[6-7]。因此讨论球面距离计算是大地主题解算的一个重要基础。

球面距离是球面上两点之间的最短距离，是经过这两点的大圆在这两点间的一段劣弧的长度。球面距离较常用的计算公式有大圆公式(Great-circle distance formulas)[8-10]、Haversine公式[10-12]等。类似大圆公式的另一种有代表性的计算方法是使用法向量代替经纬度来描述位置，通过采用点积、叉积或两者组合的三维矢量代数进行球面距离求解[13]。另可由弦长得到大圆距离，具体思路为：在地球球体上，通过三维空间连接两点之间的线段即为大圆弦长，两点之间的中心角可以根据弦长确定，大圆距离与弦长成正比。Haversine公式是球面三角学中更通用公式的一个特例，通常其与大圆公式的计算精度相当，但在某些特殊情形，Haversine公式具有更高的计算精度。以上这些大圆距离计算方法本质上都是基于球面三角关系[14-15]得出的，本文从另一个全新的角度首先针对大圆弧固有特性论述了球面大圆弧的A·r(A：Azimuth，r:Radius)约束，然后基于此约束提出球面距离的积分解算模型，并给出模型的解析解，分析奇异点(沿大圆弧的同一走向导致纬度变化量的符号发生改变的点)对模型求解的影响，进一步完善了解算模型。球面距离模型的解析解可应用于大地主题解算，同时可为航海计算及辅助决策等问题提供基础支撑。

1 球面A·r约束

经过球心的平面截得的球面圆为球面大圆。球面大圆的圆弧、劣弧分别称为球面大圆弧、大圆劣弧。通过球面上任意两点(非直径对点)有且仅有一个大圆。任意大圆上的两点A0和B将大圆分为两部分，都叫做以A、B点为端点的大圆弧。

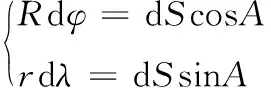
(1)

式(1)中，R为地球半径。

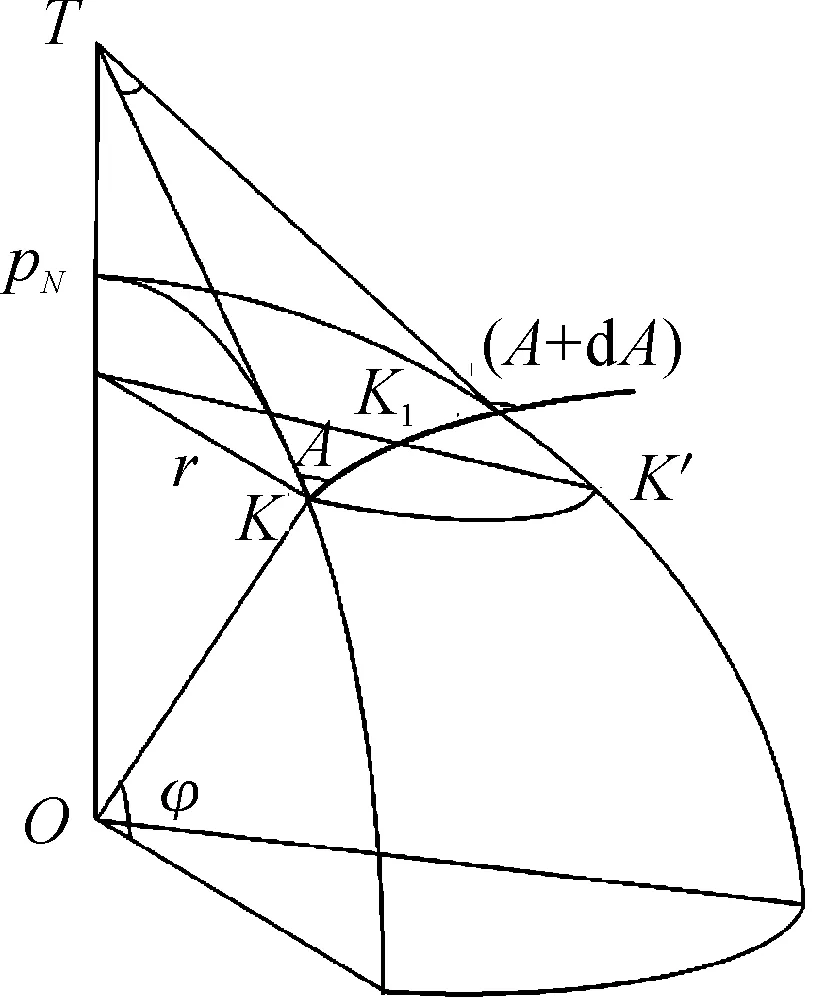
图1 A·r约束的球面示意图

即:

(2)

由平面直角三角形TKK1可得：A+dA=A+∠K1TK,即dA=∠K1TK。

因为K′十分接近K1，所以可视K′也在切平面K1TK上，于是有：

(3)

在直角三角形OKT中，KT=Rcotφ，代入式(3)得：

dA=sinφdλ

(4)

结合式(2)可得：

dA=tanAtanφdφ

(5)

将平面K1K′O从球体中分离，如图2所示。

图2 纬度变化引起的Rdφ与dr关系示意图

定义纬度增大的方向为“+”，随着纬度的增大，等纬圈半径减小，故dr与dφ异号。

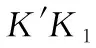
sinφ·Rdφ=r1-r=-dr

(6)

故

(7)

即rcosAdA+sinAdr=0。

积分得A·r约束条件为：

rsinA=C

(8)

式(8)中，C为与大圆弧对应的常量。

因此大圆弧上任意一点均满足该条件，即球面A·r约束为：

r1sinA1=r2sinA2=…=rnsinAn=C

2 基于球面A·r约束的大地距离解算模型及其解析解

如图3所示，pN为北极，p1、p2分别为球面上两点，其球面纬度分别为u1、u2，球面经差为Δω，两点之间的球面距离|p1p2|为δ，α1、α2为对应的球面方位角。

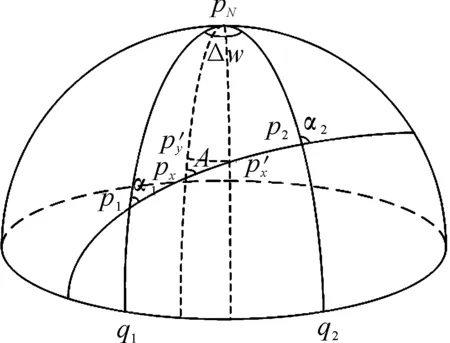
图3 球体大圆

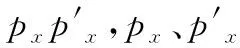
(9)

对式(9)积分，求得大圆弧p1p2的长度为：

(10)

大圆弧上每一点的方位角A不同，但都满足式(8)球面A·r约束条件。

由p1点的球面纬度与球面方位角可求得大圆弧常数C，即：

C=R·cosu1·sinα1

(11)

将式(8)、(11)代入式(10)可得：

(12)

对上式的不定积分进行换元积分可得：

(13)

最终得到大圆弧长计算公式为：

(14)

3 模型奇异点的存在问题

这种积分求取两点间球面距离的方法不需要两点的经度或经度差信息，只需两点的球面纬度及其中一点的大圆弧方位角。但此种方法适用于两点之间大圆弧上不存在大圆顶点的情况，下面对模型存在奇异点的原因进行分析。

如图4所示，pa、pb为球面大圆弧上两点，pv为此大圆弧其中一个顶点，则可得两点间球面距离公式为：

(15)

式(15)中第二部分积分在积分区间[uv,ub]上，du始终为负值，而被积函数式中为正，因此式(15)又可表示为：

(16)

由此得出结论：若大圆弧上的连续点的纬度值非单调，则式(12)中的纬度变化量du时正时负，大圆距离的积分结果会偏离实际值。

图4 奇异点的示意图

因此式(12)需改写为：

(17)

由大圆特性可知，南北半球各有一个大圆顶点，且两者的纬度相同，经度相差180°。假设两点之间大圆弧p1p2上存在一个大圆顶点pv(uv,ωv)，进一步有：

(18)

在大圆顶点pv处，球面大圆与子午线正交，球面方位角αv=90°，根据式(11)可得pv的纬度有如下关系：

cosuv=cosu1·sinα1

(19)

由球面三角形公式有：

cosα1=cosΔωv1·cos(π-αv)+

(20)

cosα2=cosΔωv2·cos(π-αv)+

(21)

可得大圆顶点pv与点p1、p2的经差分别为：

(22)

(23)

由Δωv1、Δωv2、Δω可知大圆顶点是否在p1p2上，有：

(24)

4 解算模型的有效性检验

综上所述，可最终确定球面大圆距离的求解公式：若大圆顶点pv在两点之间大圆弧上，球面距离求解公式为式(14)；若大圆顶点pv在两点之间大圆弧之外，球面距离求解公式为式(18)。

为验证积分模型的有效性，将本模型的计算结果与球面三角公式解算的大圆距离在Matlab中进行比对。固定其中一点p1(120°E,86°N)，p2经度变化范围为[120°E,122°E]，纬度变化范围为[83.5°N,85.5°N],得大圆距离解算值及解算误差分别如图5、图6所示。此处取地球半径R=6 377 830 m。

图5 经纬度变化区间内的大圆距离

图6 经纬度变化区间内的大圆距离比对差值

通过研究在p2点的经纬度变化范围内积分模型解算的球面距离如图5所示，与球面三角公式的比对差值如图6所示。第二种情况研究了高纬度下球面距离的准确性问题，球面距离最大约为2.7×105m，随着球面距离的增加，差值略有增大，但差值最大值控制在1×10-7m左右。可见此模型求解球面距离具有非常高的可靠性。

上述情况中不涉及奇异点问题，为研究奇异点存在情况下模型的解算准确性，选取了如表1所示的几种典型奇异点存在情况，计算球面要素并进行大圆顶点的位置判断，给出模型的解算误差。表1中第一列是在两点纬度相差非常小的情形下得到的距离求解结果，第二列是在高纬度下同纬度两点的解算结果，第三列是两点长距离情形下得到的解算结果，3种情形下距离解算误差都控制在1×10-7m以内。经验证在两点同经度或同纬度及长距离的情况下积分解算模型依然有效。

表1 几种典型奇异点存在情况下球面元素

5 结论

提出的基于A·r约束的大地距离解算模型能够有效解算大地距离，且计算精度与球面三角公式相当。球面距离模型应用不受使用条件限制，在高纬度地区或同纬度、同经度等情况下能保证较高的精度。球面距离模型的解析解可应用于大地主题解算，同时可为航海计算及辅助决策等问题提供重要支撑。