基于密码学困难问题的《信息安全数学基础》教学模式探索
2020-03-05周洁韩静
周洁,韩静
(西华大学计算机与软件工程学院,成都610039)
0 引言
随着计算机和互联网技术的快速发展,含有军事、政治、经济等敏感内容的信息在网络上被广泛传输。由于互联网的开放性,攻击者利用网络非法获取各种信息的事件时常发生,给国家和人民带来了极大的威胁。信息安全受到了人们越来越多的关注。在中央网络安全和信息化领导小组第一次会议上,习近平总书记明确指出,网络安全和信息化是事关国家安全和国家发展、事关广大人民群众工作生活的重大战略问题,要从国际国内大势出发,总体布局,统筹各方,创新发展,努力把我国建设成为网络强国[1]。国内越来越多的高等院校开设了信息安全专业。信息安全是一个综合性很强的交叉学科,涉及密码学、计算机、通信、控制、人工智能、安全工程、人文科学、法律等诸多学科[2]。由于良好的数学基础有利于信息安全专业的学生深入开展密码学、网络攻击与防御、网络协议分析等课程的学习,因此国内大部分院校都将《信息安全数学基础》这门课程作为信息安全专业人才培养方案中的必修课。
1 《信息安全数学基础》课程特点
《信息安全数学基础》是信息安全专业的一门核心基础课,授课对象是具有一定高等数学、线性代数基础的大学二年级学生,授课学时为40 学时。本课程主要涉及数论基础、抽象代数基础、椭圆曲线基础等三个方面的知识[3-4]。
在数论方面,主要包括整除、素数、最大公因数、同余、同余式、平方剩余、指数和原根等的基本概念和性质;Euler 定理、Fermat 定理、中国剩余定理及二次互反律等重要定理;以及欧几里得除法、素数的判定、因式分解、模重复平方计算法等重要算法。内容多,知识杂,章节的关联性较弱,核心定理的证明技巧性强。
在抽象代数基础方面,主要包括群、子群、循环群、陪集、环、零因子、理想、域等众多概念及性质。内容抽象,环环相扣,需要记忆的知识点较多,学习难度大。
在椭圆曲线基础方面,主要包括椭圆曲线的基本概念,椭圆曲线上的加法运算法则,及椭圆曲线密码系统。这部分内容难度大,内容深,知识广。由于课时的限制,本部分内容在课堂上主要讲解基本概念,更多的内容需要在教师的引导下,学生课下自主学习。
通过对本课程的学习,可以使学生系统地掌握信息安全学科涉及的数学基本概念和基本原理,建立数学体系的完整概念,为后续专业课程的学习奠定基础。
2 《信息安全数学基础》课程现状及存在的问题
《信息安全数学基础》课程中涉及众多的定义、性质、和定理,理论性强,内容抽象[5],对于工科学生而言难度较大,学生容易望而生畏,缺少学习的热情及主动性[6]。笔者结合近两年本课程的授课经验来看,主要存在以下几个问题。
(1)教学方法单一,难以调动学生积极性。
由于课时的限制,为了在有限的课时中完成教学任务,传统的教学方法主要采用以课堂教师讲授为主,课下学生完成课后作业的教学模式,授课手段多为PPT 演示或黑板板书[7]。本课程理论性强,内容枯燥,在传统的教学方法下无法调动学生的积极性,容易使学生产生畏难情绪,缺少学习的热情。
(2)课程内容分散,缺少主线
本课程主要包括整数的可除性、同余、同余式、二次同余式与平方剩余、原根、基本代数、有限域、椭圆曲线等八个章节[3],内容比较分散,学生难以建立起各个章节之间的联系,容易学了后面的知识而遗忘前面的知识,授课过程中缺少一根主线把各章节的内容联系起来。
(3)考核形式单一,重理论而轻实践
在课程考核方面,目前大多数学校主要采用考勤、作业、期末闭卷考试的考核形式,着重对学生的理论知识进行考核。学生上课听课,下课完成作业,缺少对动手能力的培养。在这种考核形式下,学生只是掌握了本课程的数学原理,缺少对本课程和信息安全后续课程联系的认识,缺少实践,不利于引导学生自主学习密码学等其他专业课程。
笔者在本课程的教学过程中积极寻求教学改进,结合课后与学生的交流及反馈情况,提出了一种基于密码学困难问题的《信息安全数学基础》教学模式,有效的提高了学生的积极性,增强了课程的连贯性,并加强了学生运用数学原理解决信息安全中实际问题的能力。
3 基于密码学困难问题的教学模式
根据密钥类型的不同,密码体制分为对称加密体制和公钥加密体制。在对称加密体制中,加密密钥和解密密钥是相同的或者彼此之间是容易确定的;在公钥加密体制中,加密密钥和解密密钥是不同的且由加密密钥得到解密密钥是不可行的[8]。其中,大部分公钥密码体制的安全性主要是基于三个数学上的计算困难问题:大整数因式分解问题、离散对数问题、椭圆曲线离线对数问题。本节将提出一种以密码学困难问题为主线的《信息安全数学基础》课程的教学模式,如图1所示。
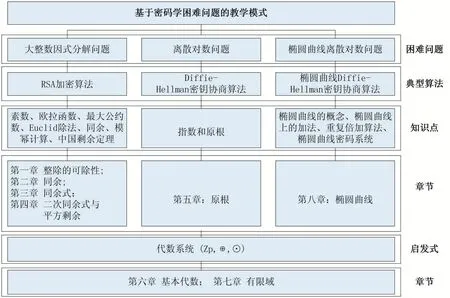
图1 基于密码学困难问题的教学模式
3.1 大整数因式分解问题
大整数因式分解问题是指,给定由两个大素数相乘而得到整数n,求n 的素因子p 和q 使得n=pq成立。基于大整数因式分解问题的代表性密码算法有RSA 加密算法。RSA 加密算法分为密钥生成过程、加密过程、解密过程,具体算法过程如下[3]。
密钥生成过程:
(1)随机产生两个不同的大素数p 和q ;
(2)计算n=pq 和n 的欧拉函数φ(n);
(3)随 机 选 取 一 个 整 数 e,1 <e <φ( n ),使 得
(4)计 算 唯 一 的 整 数 d,1 <d <φ( n ),使 得ed ≡1(mod φ(n));
(5)生成的公钥为Ke=(n,e),私钥为Kd=d。
加密过程:
(1)消息发送者从认证中心等地方取得消息接收者的公钥Ke=(n,e);
(4)消息发送者把整数c 转换成密文信息并发送给消息接收者。
解密过程:
(1)消息接收者将密文信息转换为整数c;
(2)消息接收者运用私钥 Kd=d 恢复整数m=Kd(c)≡cd(mod n);
(3)消息接收者将整数m 转换成明文信息。
RSA 算法的安全性在于已知整数n ,计算出n的因式分解是n=pq 是困难的。如果攻击者想要从公钥信息中计算出私钥Kd=d,则需要知道n的欧拉函数φ(n),而在不知道n 的因式分解的情况下,计算是困难的。
RSA 加密算法涉及《信息安全数学基础》课程中的素数、欧拉函数、最大公约数、Euclid 除法、同余、模幂计算、中国剩余定理等知识点,主要包括在本课程的第一章、第二章、第三章、第四章中的内容。因此,在详细讲解这四章内容之前,可以先引出RSA 加密算法的步骤,让学生回答哪些概念、步骤是不理解的,然后让学生带着问题学习前四章的内容,事半功倍。
3.2 离散对数问题
离散对数问题是指,给定 q 阶有限循环群G=<g >的一个元素β ∈G,求整数x ∈Z*q,使得β=gx成立。基于离散对数问题的代表性密码算法有Diffie-Hellman 密钥协商算法。Diffie-Hellman 密钥协商的目的是通信双方希望在一个公开信道中协商出一个随机的共同密钥。通信双方已知一个大素数 p 及模p 的原根g,协商的具体步骤如下[3]。
(1)用户A 产生一个随机数 xA作为私钥,1 ≤xA<n,计算gxA并发送给B;
(2)用户B 产生一个随机数 xB作为私钥,1 ≤xB<n,计算gxB并发送给A;
(3)用户A 利用自己的私钥xA和接收到的gxB计算,用户B 利用自己的私钥xB和接收到的gxA计算
Diffie-Hellman 密钥协商的安全性在于即使攻击者从公开信道中获得gxA和gxB,由于离散对数问题的困难性导致攻击者计算出共同密钥gxAxB是困难的。
Diffie-Hellman 密钥协商算法涉及《信息安全数学基础》中第五章指数和原根的内容。因此,在详细讲解第五章内容之前,先向学生介绍Diffie-Hellman 密钥协商算法的实用性及算法步骤,询问学生对于算法的认识,引出“什么是原根?”的问题,让学生带着问题和兴趣学习第五章的内容。
3.3 椭圆曲线离散对数问题
椭圆曲线离散对数问题是指,已知有限域Fp上的椭圆曲线点群:

点P=(x,y)的阶为一个大素数,给定点Q ,求整数x,使得xP=Q 成立。基于椭圆曲线离散对数问题的代表性密码算法有椭圆曲线Diffie-Hellman 密钥协商算法。椭圆曲线Diffie-Hellman 密钥协商算法与Diffie-Hellman 密钥协商算法的步骤很相似,不同点在于椭圆曲线Diffie-Hellman 密钥协商算法的所有运算都是在椭圆曲线上进行的。算法的具体步骤如下[3]。
(1)用户A、B 商定好参数:E 表示椭圆曲线,n表示椭圆曲线点群上基点P 的阶,Fq表示有限域;
(2)用户A 产生一个随机数 dA作为私钥,1 ≤dA<n,计算QA=dAP 并发送给B;
(3)用户B 产生一个随机数 dB作为私钥,1 ≤dB<n,计算QB=dBP 并发送给A;
(4)用户A 利用自己的私钥dA和接收到的QB计算dAQB,用户B 利用自己的私钥dB和接收到的QA计算dBQA;
(5)用户A 和用户B 协商出的共同密钥为KAB=dAdBP=dAQB=dBQA。
椭圆曲线Diffie-Hellman 密钥协商算法的安全性在于即使攻击中获得了QA和QB,由椭圆曲线离散对数问题的困难性导致求解出协商的共同密钥dAdBP 是困难的。
椭圆曲线Diffie-Hellman 密钥协商算法涉及《信息安全数学基础》课程中椭圆曲线的概念、椭圆曲线上的加法、重复倍加算法、及椭圆曲线密码系统等内容,主要包含在本课程的第八章。通过第一章、第二章、第三章、第四章的学习后,学生对密码系统已经有一定的掌握,因此在第八章的教学过程中可以采用翻转课堂的形式,在教师讲解了椭圆曲线基本概念及椭圆曲线上的运算后,让学生查阅资料自主学习椭圆曲线密码系统,并以小组为单位分享学习的内容。
3.4 抽象代数基础
抽象代数基础是《信息安全数学基础》课程的重要组成部分,这部分内容概念多、内容抽象,难度较大。通过前面章节的学习,学生已经熟悉集合及模p 加法⊕和模p 乘法⊗:

乘法逆元:当p 是素数时,对于集合Zp中的任何非零元素,存在∈Zp,使得
在探索了以上11 条性质过后,可以自然地引出抽象代数基础中群、环、域的概念[3]。
定义1(群):设G 是一非空集合。如果在G 上定义了一个代数运算,称为乘法“ · ”,记为a·b,而且这个运算满足下列条件,那么代数结构( )G, · 称为一个群:
(1)封闭性:∀a,b ∈G,有a·b ∈G;
(2)结合律:∀a,b,c ∈G,有(a·b)·c= a·(b·c);
(3)单位元:∃e ∈G,s.t. ∀a ∈G,有e·a=a·e=a;
(4)逆元:∀a ∈G, ∃b ∈G,使得b·a= a·b=e。
在讲解了群的定义后,引导学生发现集合Zp及其上的代数运算“ ”构成的代数结构(Zp,⊕)满足封闭性、结合律、单位元、逆元这四条性质,因此(Zp,⊕)是一个群。同时,通过让学生思考代数结构(Zp,⊕)是否是一个群的问题来加深对群概念的理解。
在讲解了群的基本概念及性质、子群、陪集、同态、循环群等内容后,可以再利用学生熟悉的代数系统(Zp,⊕,⊗) 引出另一个抽象代数基础中的重要概念“环”。
定义2(环):设R 是一非空集合,在R 上定义了加法和乘法两种代数运算,分别记为“ + ”和“ · ”。如果代数结构(R, +, ·) 具有如下性质:
(1)(R, +)是一个交换群;
(2)R 对于乘法是封闭:∀a,b ∈R,有a·b ∈R;
(4)分配律成立:∀a, b,c ∈R ,有a·(b+c) = a·b+a·c,(b+c)·a= b·a+c·a;
则称(R, +, ·)为一个环。
在介绍了环的定义后,引导学生对比代数结构(Zp,⊕,⊗)上的性质,很容易发现(Zp,⊕,⊗)就是一个环。从学生熟悉的具体的代数结构(Zp,⊕,⊗)出发,有利于学生对于抽象概念“环”的理解,并可以用实例介绍环的零因子、子环等相关概念,提高学生对于环的概念及性质等内容的掌握程度。
类似地,在讲解了环的基本概念、子环、环同态、理想、多项式环等概念及性质后,可以再利用代数结构(Zp,⊕,⊗)引出“域”的概念。
定义3(域):若R 是一个环,并且R*=R{ }0 对于乘法构成一个交换群,则称(R, +, ·) 为一个域。
通过前面对群和环内容的学习,学生很容易发现当p 是素数时,代数结构(Zp,⊕,⊗)是一个域。
笔者从近年来的授课经验来看,工科学生普遍存在抽象概念的理解能力较弱的问题。群、环、域等的概念比较抽象,通过先引入学生熟悉的代数结构(Zp,⊕,⊗),可以使学生对群、环、域的概念有了初步的具体认识,在此基础上再进行抽象代数基础内容的讲解,由浅入深,由抽象到具体再到抽象,可以使学生更好的掌握第六章基本代数及第七章有限域内容。
4 结语
本文以密码学上的数学困难问题为主线,有效地将《信息安全数学基础》课程中的数论基础、抽象代数基础、椭圆曲线基础三部分的内容连接起来,增强了课程的整体性,内容从具体到抽象,有利于学生对各个知识点融会贯通、举一反三,增强对课程的记忆力及理解力。同时,在教学过程中结合PPT、黑板板书、学生自学、翻转课堂等多种教学形式,提高了学生的学习热情及自主性。在以后的教学过程中,笔者将加强信息安全数学基础理论与信息安全实践的结合,让学生学以致用,提升学习兴趣,深入掌握相关知识。
