基于惯性扰动与自适应调节的量子粒子群轨迹覆盖算法

2020-03-05宋凡

现代计算机 2020年2期

宋凡

（广东工业大学计算机学院，广州510006）

0 引言

无线传感器覆盖问题起源于卡内基·梅隆大学的分布式传感器网络研究组。近些年来，随着技术水平的大规模提高，对无线传感器网络的研究、开发成为计算机领域一个热点，在美国移动计算和网络会议上，无线传感器是下一个世纪面临的发展机遇[1-2]被提出，越来越多的研究机构和公司正加入到这方面的研究工作来。

我们研究的轨迹覆盖问题则是属于无线传感器覆盖问题中的一个子问题，其目的就是设置传感器覆盖路径并监测其物理环境。因此覆盖率是轨迹覆盖问题中的一个重要指标，它反映了无线传感器是否能提供满意的服务。近年来，覆盖控制方面的研究工作有一定进展[3]。

根据覆盖方式的分类，分为区域覆盖、点覆盖和栅栏覆盖几种覆盖算法。对于区域覆盖，多重k 级覆盖控制算法[4]被提出。对于点覆盖基于不交叉优势集的覆盖控制算法被提出。针对栅栏覆盖提出了基于暴露模型的覆盖控制算法。文献[5]提出一个启发性的算法：分布式探测算法PEAS。在PEAS 中，一部分传感器处于工作状态，其他传感器则处于休眠状态。传感器轮流分配工作时间，可以提高传感器的使用时间。

随着20 世纪80 年代，智能进化算法的出现引起了许多学科领域研究人员的关注，已经成为人工智能、生物、能源等交叉学科的前沿及热点领域。智能进化算法主要分为以蚁群算法[6]、粒子群算法[7]、遗传算法等。文献[8]利用遗传算法实现覆盖优化，虽然遗传算法全局寻优能力强，但收敛速度慢，难以满足实时性要求。文献[9]基于粒子群算法实现覆盖优化，但是标准粒子群算法易早熟，难以满足覆盖率的要求。

基于上述文献的研究成果，证明智能进化算法能一定程度实现覆盖优化。本文的研究工作是以基本粒子群算法为基础，通过改进和结合其他优化算法来设计轨迹覆盖优化算法。在兼顾全局搜索能力和局部搜索能力的平衡的基础上有效解决早熟及收敛过慢等问题，以实现传感器的优化配置，获得有限节点情况下的网络最大覆盖率。

本文提出一种改进的量子粒子群算法用来解决轨迹覆盖问题。首先将经典的PSO 改进型算法例如，量子粒子群算法（QPSO）[10]和全局粒子群算法（GPSO）[11]应用到轨迹覆盖问题中，并比较两者的优劣，在综合GPSO和QPSO 的基础上提出改进的算法GQPSO，再对GQPSO 的结果进行分析后，进一步提出了收敛速度和聚集程度两个因子，最终得到改进后的算法AGQPSO。

1 背景

1.1 粒子群优化算法

粒子群优化算法（Particle Swarm Optimization，PSO）由Kennedy 和Eberhart 在1995 年提出，该算法对于Hepper 的模拟鸟群（鱼群）的模型进行修正，以使粒子能够飞向解空间，并在最好解处降落，从而得到了粒子群优化算法。

PSO 从这种模型中得到启示并用于解决优化问题。PSO 中，每个优化问题的潜在解都是搜索空间中的一只鸟，称之为粒子。所有的粒子都有一个由被优化的函数决定的适值（fitness value），每个粒子还有一个速度决定它们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO 初始化为一群随机粒子（随机解），然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个极值来更新自己；第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。

1.2 量子粒子群算法和全局粒子群优化算法

量子粒子群算法（QPSO）和全局粒子群算法（GPSO）属于标准粒子群算法（PSO）的两个分支。PSO 算法在复杂问题和非线性变化问题下容易早熟，QPSO 算法采用波函数表示粒子位置，通过蒙特卡罗方法求出粒子位置，在解空间中粒子都有相应的概率到达[12-13]。而GPSO 采用一种扰动式的动态惯性权重来更新粒子速度，使得权重虽然整体呈减少趋势但是在一定范围内波动。QPSO 和GPSO 所采取的策略都使得其全局搜索能力增强。

公式（1-5）为QPSO 主要公式，公式（1）中mbest 为当前代种群所有个体最佳位置的平均值，公式（5）β为惯性权重，公式（4）L 为粒子i 到mbest 的距离，由公式（3）求得种群的吸引点pi后，可根据公式（2）求得下一代粒子的位xi（t），其中M 为种群粒子个数，D 为粒子维数，pbesti为第i 个粒子历史最优，gbest 为粒子群全局最优，u、rand 为（0，1）间的随机数。

公式（6-9）为GPSO 的主要公式，t+1 代粒子i 的位置由t 代粒子i 的位置和t+1代粒子i 的速度决定。GPSO 的速度更新方式如公式（6）所示，其中βt表示第t 代的惯性权重，rand 为（0，1）之间的随机数，βmax和βmin为惯性权重的上下限分别取值0.9 和0.4。根据文献[9]的研究，GPSO 的惯性权重呈现总体下降但局部震荡的趋势，其中φ 为扰动因子，该因子增强了在全局最优解附近搜索的随机性，取值为0.01 可以得到较好的效果。

量子粒子群算法简单且全局搜索能力强[14]，具有相应概率到达解空间内所有位置，在许多情况下，都可以针对所选问题进行改进从而生成性能更优的算法[15-16]。

2 面向覆盖问题的粒子群算法

2.1 问题定义

轨迹覆盖是指从一个拥有数条轨迹的空间中设置传感器覆盖轨迹的过程。但由于传感器数量有限，轨迹之间的组合数量过多，无法将每条轨迹都进行全部覆盖，因此轨迹覆盖需要选用可行的算法进行优化。轨迹覆盖的困难在于达到较好的覆盖效率，一条轨迹，在其转折处覆盖比在平滑处覆盖具有更高的相对覆盖率，但是容易造成传感器之间的重复覆盖。与其他轨迹组合到一起时，可能会变成多条，汇聚的复杂路线。理想的覆盖方法应该是整体路径的覆盖率高，传感器之间重复覆盖率低。

目前，虽然许多针对覆盖的算法被提出，大部分算法的目标只是提高覆盖率。传感器数量的增加虽然可以提高覆盖率，但是过多的传感器数量将导致成本高昂，也不利于后续的传感器网络维护。如何在提高可接受的覆盖率的同时，降低传感器数量，这是两个冲突的目标，可以折中选择传感器数量较少，但覆盖率相对较高的组合，用于实际的覆盖应用中。

2.2 问题建模

（1）轨迹表示

第一步生成路径，本文中，二维空间中有x，y 两个维度，沿x 维度每隔一定距离k 取一个采样点的维度值x，每个采样点根据路径生成函数生成对应的维度值y。最终生成的路径如公式（11）所示：

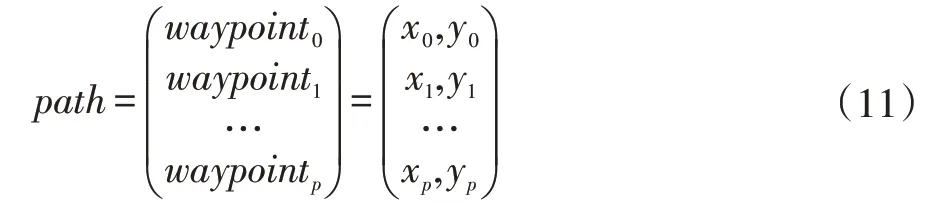
其中waypointi,i ∈[0,p]为在二维空间中生成的路径点，p 的取值如公式（12）所示，其中xMax 为路径在x维度上的最大值，k 为两个取样点之间x 维度上的距离。

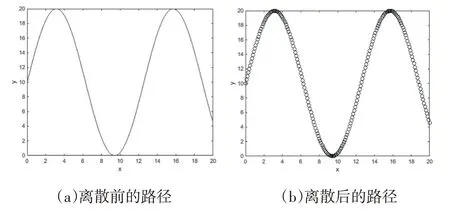
图1 离散前的原路径和离散后近似表达的路径

图1 的（b）中，每个空心点代表一个路径点，用一系列路径点近似表达了原始路径。

（2）优化目标

本文的优化目标为在有限节点下尽可能达到更高的覆盖率以及在全覆盖条件下，尽可能减少节点数目。路径离散后，覆盖率coverRatio 可以近似的表达为：

其中，Ncover为被节点覆盖一次或一次以上的路径点个数，Nsum 表达了原始路径离散化后总的路径点个数，由累加求得。当某一路径点被节点覆盖一次或多次即numcover∈N+时，对应的为1，否则为0。

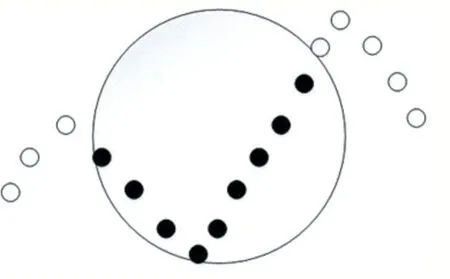
图2 判断路径是否被覆盖

由公式（16）可以判断某一路径点是否被节点覆盖。

当路径点 j 到节点 i 的欧氏距离distancenode-i,path-point-j大于节点的探测半径rnode时，节点i未能覆盖路径点j，否则节点i 覆盖了路径点j。

2.3 QPSO和GPSO实现轨迹覆盖问题的比较

（1）个体编码

粒子群算法首先初始化种群，在本文中，每个个体被编码成坐标点的矩阵。坐标点矩阵的第j 列代表了传感器网络中第j 个传感器的位置（xj，yj）。向量X，Y分别代表了矩阵的第一行（x0，x1，…，xp）和第二行（y0，y1，…，yp）（如图3）。一个粒子由一对坐标点组成（xi，yi）。一个个体由p 个粒子组成（X，Y）。坐标点矩阵的行数j 由空间维数决定，列数i 则由传感器网络中节点的个数p 决定。

假设x 维度空间大小为[xMin，xMax]，y 维度空间大小为[yMin，yMax]，则按照如下公式对每个粒子进行初始化：

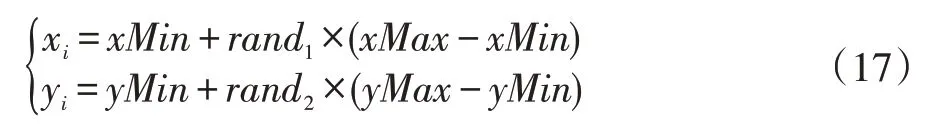
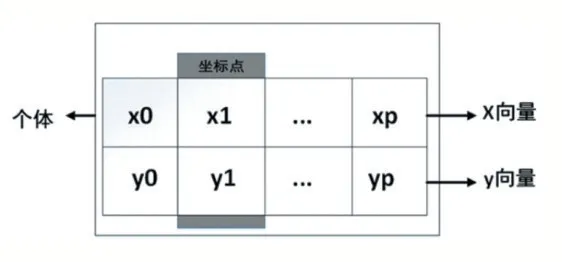
图3 粒子个体编码

xi和yi分别为第i 个节点的x 维度坐标和y 维度坐标，rand1和rand2是[0，1]间的随机数。对于GPSO 则有公式（18）所示的粒子速度初始化：

其中vMin、Vmax 分别为速度下限和上限，rand 为[0，1]间随机数。

（2）算法流程

算法流程如图4 所示。

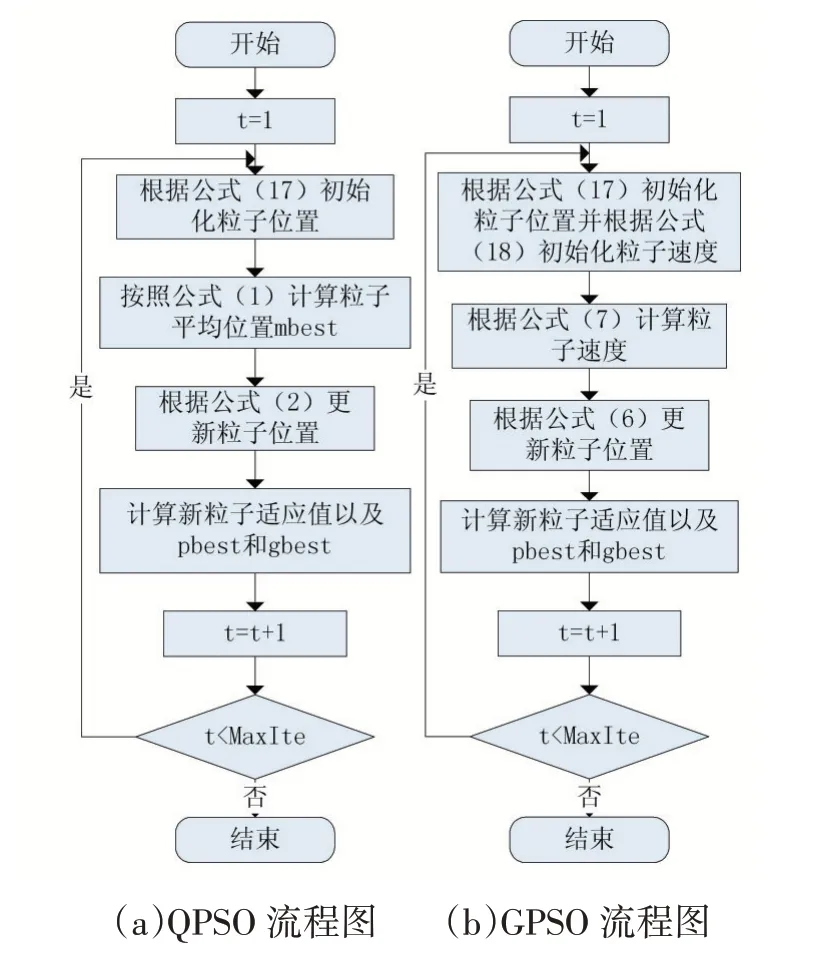
图4 QPSO和GPSO的流程图

（3）结果比较

根据本文的编码方式，将QPSO 和GPSO 应用到测试地图a 的轨迹覆盖（图5），结果如图7 所示。

3 带聚合度因子的自适应全局量子粒子群算法

3.1 QPSO与GPSO存在的问题

根据图7 的结果可知，QPSO 全局寻优能力比较强，能达到比较好的覆盖率，但是收敛速度比较慢、而GPSO 收敛速度很快但是容易陷入早熟。

图5 测试GPSO与QPSO的地图a

3.2 带GPSO惯性权重更新的GQPSO

综合比较GPSO 与QPSO 的结果，由于QPSO 优秀的全局寻优能力，本文在QPSO 的基础上进行改进。原始的QPSO 的惯性权重β 依据公式（5）线性递减，本文将GPSO 的惯性权重更新方式应用到QPSO 中，依据公式（8）可得到改进后的GQPSO 粒子更新方式，式中参数的取值与前面介绍QPSO、GPSO 的参数取值一致。

图6 GQPSO算法流程

图7 9 至14 个探测器数量下GQPSO、GPSO、QPSO相应覆盖率的比较

3.3 分析GQPSO的结果并提出改进算法AGQPSO

观察GQPSO 的结果发现，虽然算法收敛速度有所提高，但是最终得到的覆盖率不理想，与原始QPSO 相比并反而更差。综上，本文提出收敛速度因子s，定义为：

其中ct为第t 次迭代的全局最优粒子覆盖率ct-1为第t-1 次迭代的全局最优粒子覆盖率，s ∈[0,1]，s 越小说明收敛速度越快。定义收敛速度因子后，AGQPSO的惯性权重先采用公式（8）中的惯性权重计算方式达到快速收敛目的，如果收敛速度趋近0，则改变惯性权重的计算方式，依据公式（5）计算惯性权重。AGQPSO在前期使用GPSO 惯性权重计算方式快速迭代，当种群迭代一定代数后无法找到更好的解就使用QPSO 惯性权重计算方式，种群具有更高的全局寻优能力。

3.4 进一步改进AGQPSO

虽然AGQPSO 与QPSO 相比收敛速度更快，与GPSO 相比覆盖率更高，但是AGQPSO 的提升都只是在一方面，对此本文提出聚合度因子，进一步改进AGQPSO。

聚合度因子d 定义如下：

mbest 为第t 代粒子最好位置的平均适应度，显然，0 ＜d ≤1，d 代表了群体最优粒子的适应度到群体粒子平均适应度的比值，一定程度反映了粒子的聚集程度，当d=1 时，算法收敛。有了粒子聚集度因子，我们可以知道群体当前的聚集状态，当粒子都聚集到一起时，可以增大惯性权重β，当粒子太分散时，可以减小β 以达到控制粒子的全局搜索能力和局部搜索能力达到平衡。

其中，w1和w2分别为控制收敛速度和聚集度的权重，b=1。由图7 可知，QPSO 采取的线性惯性权重递减虽然收敛速度较慢，但是其收敛曲线稳定递进，具有较好的探索能力，而GPSO 采取的权重更新方式具有一定的不确定性，有利于跳出局部最优。从而我们采取两种方式改进AGQPSO，第一种为：完全根据公式（21）进行权重更新，第二种为在原始QPSO 权重更新方式上融合GPSO 和公式（21）中的方式更新权重。采用第二种方式，具体为：先对惯性权重β 线性减少，使得粒子稳定搜索解空间，每迭代k 代，如果收敛速度小于γ，β 就改变更新方式，每次迭代根据公式（22）计算权重概率rw，其中rand 为[0，1]间的随机数，t 为当前迭代次数，MaxIteration 为最大迭代次数。当rw小于阈值0.7时采用GPSO 的更新方式，当rw大于或者等于0.7 时采用公式（21）所示的更新方式。GPSO 的更新方式具有一定的随机性，有助于跳出局部最优，每当进行一次随机性较大的惯性权重更新以后，采用收敛速度因子和聚集度因子来评估群体当前状态，并依据公式（21）根据评估结果对权重进行计算，调整粒子位置。这样随着迭代次数增加rw小于0.7 的可能性降低，种群随机性降低收敛趋于稳定，使群体能够最终找到较好的结果。所得的结果如图8，在分析rw时，我们选取了0.5、0.6、0.7、0.8 和0.9 共5 个阈值，根据实验结果选择0.7作为最终取值。

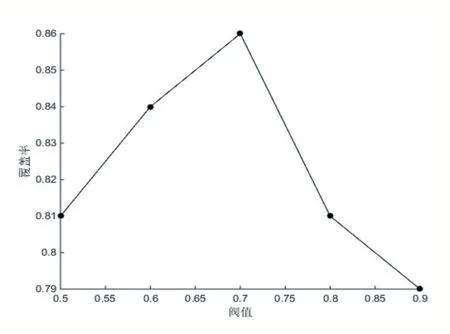
图8 AGQPSO 在地图6 取不同阈值时的覆盖率

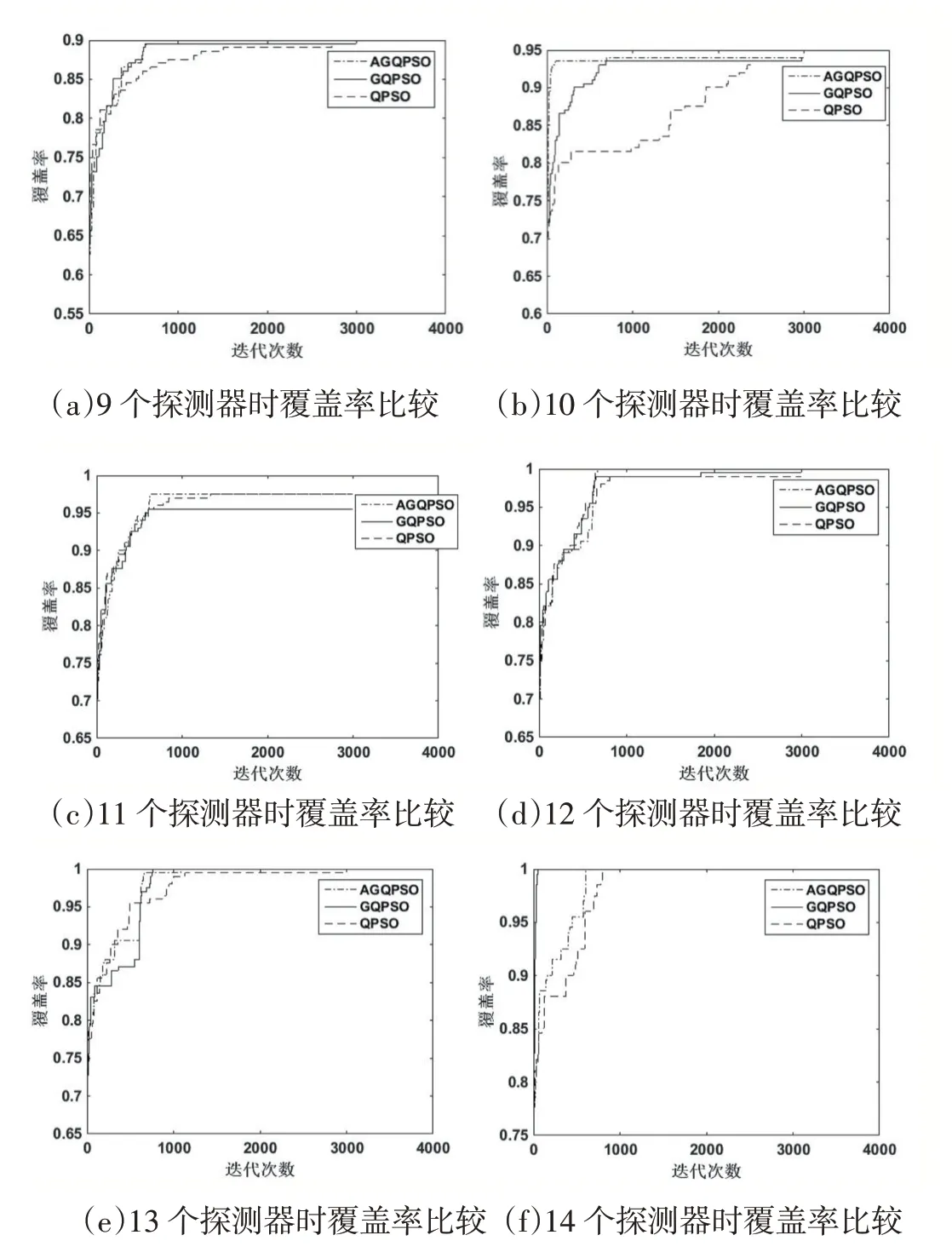
图9 9 至14 个探测器数量下AGQPSO、GQPSO、QPSO相应覆盖率的比较

由图9 可知：最终改进的AGQPSO 与GQPSO 相比在9、10、11、12 个探测器个数时都能取得更高的覆盖率，在13、14 个探测器个数时都能达到全覆盖。AGQPSO 与QPSO 相比在所有情况下，收敛速度和覆盖率都更好。

3.5 完整算法流程

步骤1）对群体中的每个粒子的位置初始化

步骤2）按预设的迭代次数进行循环

2.1）对群体中每个粒子：

根据收敛速度判断群体是否停滞不前，无法快速找到更好的结果

1）否，执行公式（5）的惯性权重更新规则

2）是，改变惯性权重更新规则

根据公式（22）结果分别采用（8）和公式（21）所示的惯性权重更新规则计算每个粒子的适应值，更新粒子的pbest，gbest计算群体的收敛速度和聚合度，并以此计算惯性因子

根据公式（2）计算粒子下一代位置

步骤3）找到取得gbest 的粒子，并将其所在位置作为结果返回

算法中的学习系数c1和c2与标准中的设置相同，c1=c2=1.0。

4 实验设计及数据分析

4.1 数据集与参数设置

在比较试验中，每种算法的粒子个数都为100 个，最大迭代次数为3000 代。实验分别采用QPSO（量子粒子群算法）、GPSO（全局粒子群算法）和AGQPSO（本文提出的算法），在6 种不同的地图上分别测试30 次所得的平均覆盖率作为最终结果来比较（如表2 所示）。参数取值如表1 所示。

表1 AGQPSO 中的参数值

4.2 实验结果

如表1 和图7 所示，比较QPSO 与GPSO 我们发现QPSO 的迭代速度通常慢于GPSO，但是覆盖率优于GPSO，特别的在实验1 下探测器个数为10 个时，GPSO的迭代次数相比QPSO 少了1000 代，结果仅仅差了2.4%，说明GPSO 虽然覆盖率不如QPSO 但是结果相差不大，且收敛速度很快。如图9 所示，结合了QPSO和GPSO 优点的GQPSO 在收敛速度上优于QPSO，在覆盖率上优于GPSO，GQPSO 在QPSO 和GPSO 的优势上有所折中，但是补充了各自的缺点。如表2 及图9所示，在GQPSO 上进一步改进的AGQPSO 在引入了聚合度和收敛速度这两个因子后，收敛速度及覆盖率相比于QPSO 和GPSO 都有不错的提升，不仅在覆盖率上超过了QPS O，在收敛速度上也不差于GPSO。