构建深度课堂 提升数学能力
2020-03-04吕琴
吕琴
【摘 要】本文以《直线与圆的位置关系(4)》为例,探索深度学习理念下深度课堂的构建。深度课堂体现在知识理解深刻、对话交流深入、情感体验贴切、学科能力生长等多个维度。构建深度数学课堂,促进学生深度学习,激发学生学习热情,锻炼学生思维能力,发展学生数学核心素养。
【关键词】深度课堂;数学能力;核心素养
一、教学目标
1.知识目标:了解切线长的定义,掌握切线长定理,并利用它进行有关的计算;在运用切线长定理的解题过程中,进一步渗透方程的思想,熟悉用代数的方法解几何题。
2.能力目标:经历画图、度量、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,培养学生有条理地、清晰地阐述自己的观点的能力。
3.素质目标:初步学会从数学的角度提出问题、理解问题,并能运用所学的知识和技能解决问题,发展应用意识。在解题中形成解决问题的基本策略,体验问题策略的多样性,发展实践能力与创新精神。
4.情感与态度目标:了解数学的价值,对数学有好奇心与求知欲,在数学学习活动中获得成功的体验,锻炼克服困难的意志,建立自信心。
二、教学重点及难点
教学重点:理解切线长定理
教学难点:应用切线长定理解决问题
三、教学方法
教学方法采用引导发现法,辅之以讨论法。本节课是概念、定理、解题的教学,因此,要利用概念模式元、定理教学模式元、解题教学模式元的有机组合,完成本节课的教学。
四、教学过程
1.操作
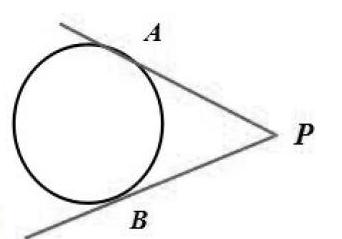
经过⊙O外一点P画⊙O的切线,并思考过圆外一点可以画圆的几条切线?
【设计意图】学生经历操作观察的过程,可以直观了解过圆外一点可以画圆的两条切线,也为引入“切线长”和“切线长定理”做好铺垫。教学时学生先尝试,然后老师再进行示范。
概念:在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长。
根据概念,解决下面两个问题:
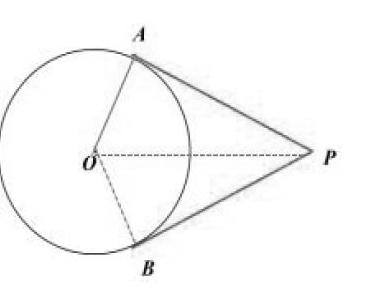
(1)如图,PA和PB分别与⊙O相切于点A、B,点P到⊙O的切线长可以用哪一条线段的长来表示?(线段PA或线段PB)
(2)切线与切线长的区别是什么?
(切线是一条与圆相切的直线;切线长是指切线上某一点与切点间的线段的长。)
【设计意图】此处通过学生思考得出结论,再次加深学生对概念的理解,也使学生了解切线长与切线的关系。教学时教师在板书定义之后,通过对话交往,引导学生把对概念的感性认识上升到理性认识,然后在图形中进行识别,从而认识概念的本质特征,理解概念的外延。在对话中,教师以民主的精神、平等的作风、宽容的态度、真挚的爱心和悦纳的情怀对待学生,在相互倾听、接受和共享中获得知识,使教学相长。同时由这个结论教师适时引出探索。
2.探索
(1)度量线段PA和PB的长度;
(2)猜想:线段PA和PB之间的关系;
(3)寻找证明猜想的途径;
(4)还能得出哪些结论?并把它们归类。
【设计意图】定理教学的方式是学生自主探索,相互交流相结合。首先出示探索步骤的前2个,等学生猜想出结论后,再明确仅凭观察、度量、猜想并不能说明结论的正确性,还需证明结论的正确性,同时激励学生寻找证明猜想的途径。之后,再让学生探索更多的结论。随着一环紧扣一环的探索问题的深入,学生通过自主地发现问题、信息搜集与处理、表达与交流等探索活动,深度学习深度思考,获得知识、技能,以及积极的、深层次的体验,从而促进学生探究能力的发展。
(5)运用图形运动的方法证实结论。
【设计意图】在圆的许多重要性质中,圆的对称性(轴对称、中心对称及旋转不变性)是最基本的性质,这里运用图形运动的方法对“切线长定理”进行证实,强化学生对圆的对称性的认识。
3.归纳
线段相等:PA=PB; OA=OB;
角相等:∠APO=∠BPO; ∠AOP=∠BOP;
垂直关系:OA⊥PA; OB⊥PB;
三角形全等:△OAP≌△OBP。
【设计意图】培养学生总结归纳概括能力及表达能力,把知识纳入系统,便于学生存储、提取和应用。
定理:过圆外一点所画的圆的两条切线长相等。
切线长定理为证明线段相等提供了新的方法。
你会写出定理的符号语言吗?
数学符号语言:∵PA、PB分别是⊙O的切线,点A、B分别为切点,∴PA=PB,
【设计意图】数学符号语言能使定理的本质含义变得更清晰更直观,课堂上注重数学符号语言的教学,有助于培养和提高学生的数学符号意义获得能力。
4.巩固
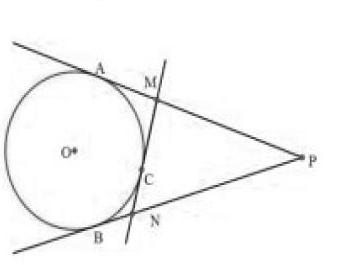
(1)如图,PA、PB是⊙O的切线,切点分别为A、B,过劣弧AB上一点C作⊙O的切线分别交PA、PB于点M、N,写出图中所有相等的线段 。
若PA=12cm,则△PMN的周长等于 cm。
(2)已知如图,PA、PB分别与⊙O相切于点A、B,PO与⊙O相交于点D,且PA=4cm,PD=2cm。求半径OA的长。
(3)如图,在以点O为圆心的两个同心圆中,大圆的弦AB、AC分别与小圆相切于點D、E。AB与AC相等吗?为什么?
【设计意图】及时巩固所学知识,利用定理进行有关的计算和证明。在第(2)题中进一步渗透方程思想,熟悉用代数的方法解决几何题。
5.小结
(1)通过本节课的实践、探索、交流,你有哪些收获?
【设计意图】课堂小结有利于学生掌握本节的重点内容,培养学生总结归纳的能力和语言表达能力。
(2)连结两个切点AB交OP于点C,又能得出什么结论?
【设计意图】在课堂探索结束之时,鼓励学生继续进行课后探索。以“课虽尽,思不止”之效,诱发学生深入探究的积极性,引起学生课后的回味和思索,并深化课堂教学内容。
【参考文献】
[1]鞠文灿.追求“深度学习”的课堂时间样本[J].江苏教育研究,263期
[2]刘瑞红.基于深度学习发展数学核心素养的教学探索[J].求学,2019(4),14-17
(苏州工业园区星澄学校,江苏 苏州 215000)
