基于变形特征值及特征状态参数的金属材料高温变形本构方程

(天津钢管集团股份有限公司技术中心，天津 300301)

0 引 言

金属热变形流变应力是金属材料塑性加工工艺优化及机械设计与研究的重要参数之一，其大小受到变形程度、变形温度、应变速率、合金化学成分与晶粒尺寸等因素的影响，也是变形体内部显微组织演变的综合反映。然而到目前为止，流变应力仍无理论解析式，只能通过诸如拉伸法、扭转法和压缩法等试验方法来求得，且一般以曲线的形式给出，不能直接应用于热轧、拉拔、挤压等实际生产过程中变形抗力的计算。为此，很多学者建立了不同材料的流变应力本构方程及不同类型的流变应力本构模型。目前，金属材料的高温流变应力本构方程大致可分为3类：一是基于试验结果，利用某种数学函数建立的经验方程，例如Voce方程[1]、Misaka方程[2]、Sah方程[3]、Johnson-Cook方程[4]等；二是基于物理理论(如位错理论)建立的唯象方程，例如Bergstrom方程l[5]、Estrin-Mecking方程[6]、Zerilli-Armstrong方程[7]、Follansbee-Kocks方程[8]、Preston-Tonks-Wallace方程[9]；三是分段描述动态回复和动态再结晶的两阶段方程，即以经验方程或唯象方程模型构建动态回复阶段的本构方程，再将描述由动态再结晶引起加工软化过程的Avrami方程合并到所构建的本构方程中，形成一个能够描述动态再结晶阶段的方程，例如Sellars-Tegart-Garofalo方程[10]、Laasraoui-Jonas方程[11]等[12-18]。

经验方程的优点是数学形式简单，能够描述金属材料热塑性变形时从动态回复阶段到动态再结晶阶段的应力-应变关系，采用回归法容易求解方程中的常数；其主要缺点是不能反映动态再结晶对流变应力的影响。唯象方程以位错应变理论为基础，构建的模型能够精确描述金属材料应变硬化和动态回复阶段的应力-应变关系，但亦不能反映动态再结晶对流变应力的影响。两阶段方程是目前金属材料热加工过程中构建的主要高温变形本构方程，能够描述高温变形过程中出现的动态再结晶现象，并且具有较好的流变应力预测精度，但是该类方程将应力-应变曲线分段描述，不方便实际热加工过程中流变应力的预测计算。并且，该类方程材料常数的确定十分复杂，导致计算所得应力-应变曲线与试验曲线存在较大的误差。作者在分析商业纯铝、无氧铜及超低碳钢的高温应力-应变曲线的基础上，采用变形特征值及特征状态参数，构建了一个新的可以连续描述金属材料高温变形应力-应变关系的唯象本构方程，包括高温变形过程方程和特征参数方程，并通过商业纯铝、无氧铜、超低碳钢的高温压缩试验，对该本构方程的计算准确度进行了验证。

1 本构方程模型

金属材料在高温塑性变形时，在低应变速率下会发生动态再结晶，其应力-应变曲线上会出现峰值应力等特征值点。据此，作者构建了两种本构方程：一是根据应力-应变曲线上的特征值构建高温变形的过程本构方程；二是构建特征值的状态方程，如LM参数状态方程、Z参数状态方程[10]、erf参数状态方程(文献[9]中方程的改进)、MTS参数状态方程[8]。

构建的高温变形过程本构方程为

(1)

式中：σ为应力；σss为动态再结晶稳态应力；ε为应变；εr为松弛应变；C为常数，取1；σp为动态再结晶峰值应力；εp为峰值应变。

当不发生动态再结晶时，饱和应力σss(e)=σss=σp。

(1) 材料高温变形过程中温度与应变速率的关系通过LM参数L可表示为

(2)

则各特征值σss，σp，εp，εr可表示为

σss/μ=σss,max-(σss,min-σss,max)×

(3)

σp/μ=σp,max-(σp,min-σp,max)×

(4)

εp=εp,max-(εp,min-εp,max)×

(5)

εr=εr,max-(εr,min-εr,max)×

(6)

式中：σp,max，σp,min，mp，σss,max，σss,min，mss，εp,max，εp,min，np，εr,max，εr,min，nr均为材料常数；μ为剪切弹性模量。

(2) 材料高温变形过程中温度与应变速率的关系通过Z参数可表示为

(7)

式中：Q为热变形表观激活能；R为气体常数。

则各特征值σss，σp，εp，εr可表示为

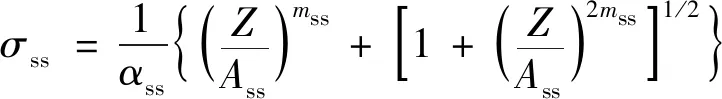
(8)

(9)

εp=BpZCp

(10)

εr=BrZCr

(11)

式中：αss，Ass，mss，αp，Ap，mp，Bp，Cp，Br，Cr均为材料常数。

(3) 材料高温变形过程中温度与应变速率的关系通过erf参数Ferf可表示为

(12)

式中：g为材料常数；Tm为熔点温度。

则各特征值σss，σp，εp，εr可表示为

σss/μ=Dss0+Dss1Ferf

(13)

σp/μ=Dp0+Dp1Ferf

(14)

εp=Ep0+Ep1Ferf

(15)

εr=Er0+Er1Ferf

(16)

式中：Dss0，Dss1，Dp0，Dp1，Ep0，Ep1，Er0，Er1均为材料常数。

(4) 材料高温变形过程中温度与应变速率的关系通过MTS参数Ss可表示为

(17)

式中：K为玻尔兹曼常数；b为柏氏矢量。

则各特征值σss，σp，εp，εr可表示为

σss=exp(Fss0+Fss1Ss)

(18)

σp=exp(Fp0+Fp1Ss)

(19)

εp=exp(Gp0+Gp1Ss)

(20)

εr=exp(Gr0+Gr1Ss)

(21)

式中：Fp0，Fp1，Fss0，Fss1，Gp0，Gp1，Gr0，Gr1均为材料常数。

2 高温变形流变应力计算及结果

2.1 材料参数计算步骤及结果

试验材料为商业纯铝、无氧铜、超低碳钢。在试验材料高温试验结果的基础上分别进行流变应力计算。其中，商业纯铝高温压缩试验数据来自文献[19]，无氧铜高温压缩试验数据来自文献[20-22]，超低碳钢高温平面压缩变形试验数据来自文献[23]。

由文献[24]可知，铝的剪切弹性模量为

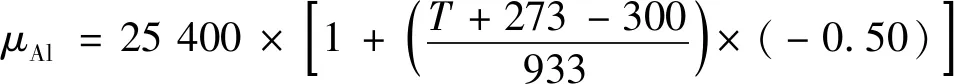
(22)

铜的剪切弹性模量为

(23)

钢的剪切弹性模量为

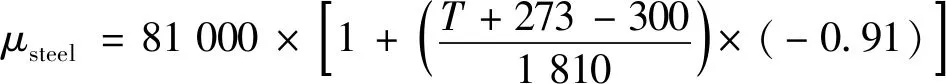
(24)

首先采用式(1)拟合应力-应变曲线，获得特征值(σss,σp,εp,εr)，然后采用式(2)～(6)、式(7)～(11)、式(12)～(16)、式(17)～(21)分别拟合LM参数方程、Z参数方程、erf参数方程、MTS参数方程，确定各参数方程中的各材料常数,结果见表1～表4。

表1 不同材料LM参数方程的材料常数Table 1 Material constants of LM parameter equation for different materials

表2 不同材料Z参数方程的材料常数Table 2 Material constants of Z parameter equation for different materials

表3 不同材料erf参数方程的材料常数Table 3 Material constants of erf parameter equation for different materials

表4 不同材料MTS参数方程的材料常数Table 4 Material constants of MTS parameter equation for different materials

2.2 高温变形流变应力计算与试验结果

将不同材料参数代入对应的参数方程，再代入式(1),即得到不同参数方程计算得到的不同材料的真应力-真应变曲线，如图1～图3所示。不同参数方程计算得到的峰值应力及实测峰值应力见图4。从图1～图4可以看出：由Z参数方程、LM参数方程、erf参数方程、MTS参数方程计算得到的商业纯铝和超低碳钢的真应力-真应变曲线与试验结果一致，计算所得峰值应力与试验值的相对误差全部处于±10%范围内；而计算得到的无氧铜在某些变形条件(例如温度500 ℃、应变速率3 s-1；温度600 ℃、应变速率3 s-1；温度800 ℃、应变速率30 s-1；温度900 ℃、应变速率100 s-1)下的计算结果与试验结果存在较大差距，计算所得峰值应力与试验值的相对误差约为15%。由于热压缩变形试验存在一定误差，并且热塑性变形的复杂性造成所建模型难以完全精确地描述所有变形条件下的流变应力行为，因此计算曲线与试验曲线存在不一致处。

图1 不同温度和应变速率下商业纯铝真应力-真应变曲线的试验结果及不同特征参数计算结果Fig.1 Test results and calculation with different characteristic parameters of true stress-true strain curves of commercial pure aluminum at different temperatures and strain rates

3 结 论

(1) 基于变形特征值(σss，σp，εp，εr)及特征状态参数(LM,Z,erf,MTS参数)，建立了一个描述金属材料高温变形的本构方程，该方程包括高温变形过程方程和特征参数方程；通过在材料的应力-应变曲线上获取特征点，采用参数方程简单拟合即可得出本构方程中材料常数与温度、应变速率的关系。

(2) 通过该本构方程计算得到的纯铝和超低碳钢的高温真应力-真应变曲线与试验结果吻合性较好，其峰值应力计算值与试验值的相对误差均小于10%，但无氧铜的达到了15%，模拟计算精度略低；该本构方程可用于预测纯铝和超低碳钢在热加工变形条件下的流变应力。

图2 不同温度和应变速率下无氧铜真应力-真应变曲线的试验结果及不同特征参数计算结果Fig.2 Test results and calculation with different characteristic parameters of true stress-true strain curves of oxygen free copper at different temperatures and strain rates

图4 不同试验材料峰值应力的实测值与不同特征参数计算值的对比Fig.4 Comparison of test values and calculated values with different characteristic parameters of peak stresses of different test materials: (a) commercial pure aluminum; (b) oxygen free copper and (c) ultra-low carbon steel