概率统计教学与高等数学知识的结合探讨

丁 李

（淮北职业技术学院 安徽淮北 235000）

一、一维连续型随机变量和概率密度

在诸多有关概率统计的教材当中[1]，首章内容普遍是古典概率，由于高中生懂得如何进行排列组合，所以便于理解，但是在学习第二章的一维随机变量时，一维离散型随机变量易于理解，不过从教师开始讲解一维连续型随机变量和概率密度内容时，学生便会碰到概率统计中的首个难题，在分析一堆随机变量的过程中，通常会设置随机变量X的概率密度函数，然后再对随机变量的另外一些性质进行分析，而这样一来便会碰到下面的题型：

例：连续型随机变量X的概率密度是f（x）=Ax’0＜x＜1，求：（1）未知常数A；（2）X的分布函数书F（x）

上面的题型在概率统计中经常会遇到，主要是使用以下的概率统计公式：

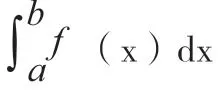
F（x）代表的是f（x）的一个原函数，不过在此种题型当中，积分的积分区间貌似均不属于确定区间[a’b]，怎样合理的在这种题型里使用牛顿-莱布尼茨公式来对学生进行讲解，学生就难以理解了，怎样使学生进行巧妙的使用呢？我们来具体的讲解一下：

（1）求常数A

（2）求X的分布函数F（x）

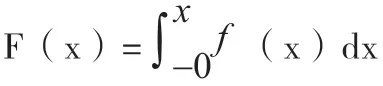
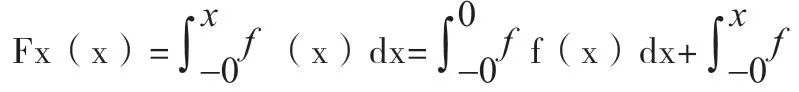
二、多维随机变量

在讲解多维随机变量的时候[2]，难免会涉及到二重积分，怎样明确积分区域，还是学生学习的一大难点，例如二维连续型随机变量（X，Y），若已知其联合概率密度f（x，y）=（x，y），（X，Y）∈D，其中（x，y）不等于0，如果想要求概率P{（X，Y）∈G}，要采用公式P{（X，Y）eG}=f（x，y）dxdy.

此时，学生很有可能误写为：P{（X，Y）∈G}=f（x’y）dxdy=（x’y）dxdy

此时运算（x’y）在区域G中的二重积分是错误的，合理的方式为：P{（X’Y）∈G}=f（x’y）dxdy=（x’y）dxdy

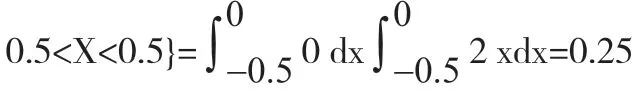
通过以上介绍，主要的目的在于通过高等数学给学生讲解概率统计中需要使用到的知识，在进行概率统计教学时，也不要觉得学生了解高等数学，就认为学生能够合理的进行运用，在概率统计教学期间应怎样进行讲解，才可以使学生合理的使用高等数学，才是最高的教学目标，也是以后在教学时所要重点研究的内容。