“三环六步”教学模式在数学文化课中的应用

李文明

（重庆市巫溪县塘坊镇中心小学校 重庆巫溪 405803）

一、理论依据

数学文化是数学知识、数学方法、数学活动、数学事件、数学意识、数学思维、数学思想、数学精神等的总和。

二、总体目标

开展趣味数学游戏，展现精典的思路，让学生发现数学的思想方法，感受到其中隐藏的数学文化。

三、初步框架

（一）总的原则：尝试原则

研究以数学文化之思想方法的“三环六步”教学模式。（在实践中，教师可不局限于六个步骤，教师可根据不同课型设计有效的课堂教学步骤。）

（二）“三环六步”的说明

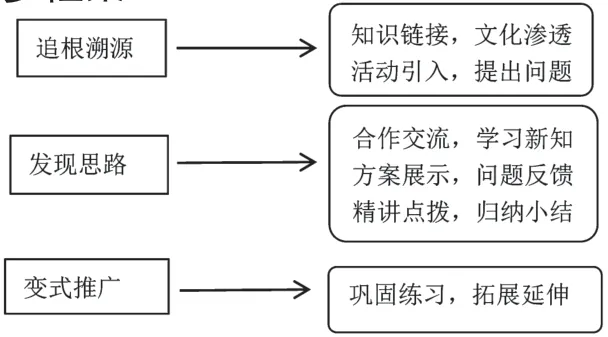
三环：追根溯源（寻找数学文化），发现思路（探索数学文化），变式推广（应用数学文化）。六步：知识链接，文化渗透；活动引入，提出问题；合作交流，学习新知；方案展示，问题反馈；精讲点拨，归纳小结；巩固练习，拓展延伸。

（三）课堂基本步骤

①追根溯源环节：◆知识链接，文化渗透；◆活动引入，提出问题。介绍数学历史，让学生从整体上认识数学的发展；讲述数学家的故事，让学生知道数学的发展是靠先辈刻苦钻研取得的。从而，引入课题提出问题。

②发现思路环节：◆合作交流，学习新知◆方案展示，问题反馈；◆精讲点拨，归纳小结。数学故事、游戏蕴含着丰富的思想方法，让学生通过各种方式，再现精妙思路，感受到隐藏于其中的数学文化。

③变式推广环节：◆巩固练习，拓展延伸。学生完成相应的变式题目，并将这一类题目的思路进行推广，让学生体会到迁移的作用。

四、教学实践

下面以《挖宝藏》为课例，来介绍“三环六步”教学模式的实施步骤和操作流程。

（一）教学目标

◆引导学生在游戏中尝试探究挖宝藏的办法，思考必胜策略。

◆感悟数字排列，渗透逆推的数学方法。

◆感受游戏中的数学思考，体验数学文化蕴含的思想方法。

教学重点：探究数字排列规律，学会逆推数学的方法。

教学难点：用数学的方法分析游戏，发现隐藏于其中的思路。

（二）教学过程

①追根溯源

◆知识链接，文化渗透

约翰·福布斯·纳什，1994年获得了诺贝尔经济学奖。他不仅爱玩游戏，更善于通过不断的学习、研究，去发现游戏背后的规律。纳什根据自己玩游戏的体会，发明了非合作博弈论，他的博弈论在经济学界作了非常重要的贡献。

设计意图：讲科学家的故事,分享他们成功的经验，了解他们成功背后付出的艰辛劳动，树立学习的榜样。

◆活动引入，提出问题

今天我给大家带来了一张藏宝图，就放在从左往右数的9号坑中，不过这份藏宝图只有玩游戏的高手才有资格获得。两人从1开始依次轮流报数。每人每次最少报1个数，最多可报2个数，谁先报到9谁就获胜。这个游戏里会有必胜的秘诀吗？

设计意图：创设游戏情境，激发学生兴趣。学生了解游戏规则后，积极思考取胜的办法。让学生明确学习任务，尝试思考解决问题。

②发现思路

◆合作交流，学习新知

四人一小组开始游戏，其中两人报数，第三人记录方案，第四人思考怎样报数才能赢？找出最后抢的那个数的特征是什么?每次报数的总个数等于什么？

设计意图：开展合作学习，明确成员的任务。学生积极参与数学游戏，充分发表自己的见解，善于倾听别人的建议，进行小组合作交流，取长补短，共同提高。

◆方案展示，问题反馈

请三个小组的学生上台展示。

A组（乙胜）

甲报的数 1 4 7乙报的数 2、3 5、6 8、9

B组（乙胜）

甲报的数 1、2 4、5 7、8乙报的数 3 6 9

C组（甲胜）

甲报的数 3 5、6 9乙报的数 1、2 4 7、8

板书：

抢的数有9、6、3。（逆推法）

设计意图：让学生汇报本组的方案，说出抢数的思路，体验探究的愉悦。教师进行板书，然后介绍逆推法。

◆精讲点拨，归纳小结。

最后抢的那个数除以3没有余数。

1加2等于3，所以就3个一组。报数时每几个一组是根据游戏规则来决定的，每次报数的总个数＝每次最少报的个数+最多报的个数。

都应该-选择后报，然后与对方保持3个数为一组的报数，对方报1个我就报两个，对方报2个，我就报1个，使得每次报数的总个数是3个。

设计意图：教师引导学生回顾解决问题的过程，找出最后抢的那个数的特征、每次报数的总个数、选择后报的规律，让学生掌握必胜的秘诀。

小结：许多游戏与数学密不可分，想要玩好游戏，动脑筋找规律，想办法占先机，就能控制全局。若不利不泄气，等待机会获胜。做游戏的主人，做生活的智者。

③变式推广

◆巩固练习，拓展延伸

两个人从1开始轮流报数，每次最少报1个数，最多可报3个数，谁先抢到12谁就胜利。（最后抢的那个数除以3没有余数，应该选择后报，每次报数的总个数是4个）

板书：

每次最少报1个数，最多可报4个数，怎样才能保证抢到15？（最后抢的那个数除以3没有余数，应该选择后报，每次报数的总个数是5个）

板书：

设计意图：练习时先巩固新知的认识，再做到逐层深入。让学生用数学的方法分析游戏，找到游戏的规律，发现隐藏于其中的思路，在变式练习中进行推广。

五、教学反思

成功之处：改变传统的“满问、满题、满灌”，学生没有思考时空的教学模式，实施以数学文化思想方法为基础的“三环六步”教学模式。学生通过自主学习探索、合作进行交流、动手操作实践，发现总数、每次报数的总个数、选择后报的规律，掌握必胜的秘诀。特别说明，此模式仅适合小学数学文化之思想方法的教学，其他模式有待进一步研究。另外，还需设计形式多样的练习题目。