一种可拆卸机心的无源驱动展开机构设计①
2020-03-04卢鹏俊郭彦彪屈二渊罗美荣
卢鹏俊,梁 渭,郭彦彪,马 进,屈二渊,罗美荣
(西安轻工业钟表研究所有限公司,西安 710061)
0 引言
可拆卸机心的无源驱动展开机构是某系列卫星伞状天线状肋展开机构展开的动力源及天线肋的锁定支撑机构,用于驱动伞状天线的展开及展开后的型面保持,同时具有展开过程冲击小、环境适应性强、可靠性高、可操作性强的特点。
目前,国内在轨使用的该类型机构均为一体化结构,地面维护性、互换性差,调试周期长。
天线在卫星发射阶段处于收拢状态;卫星入轨后,解除锁定装置,无源展开机构驱动天线缓慢展开。
无源展开机构主要由铰链架组件、机心组件、锁定装置等组成。无源展开机构以铰链架组件作为支撑,铰链架组件包含基体与展开部件两部分,基体实现与天线的连接,承载机心组件与锁体部件。机心安装在基体上,为天线的展开提供动力。在无源展开机构展开的整个过程中基体与天线底座固定不动,展开时展开部件转动,展开到位后锁定装置锁定,如图1为无源展开机构展开状态示意图,图2为无源展开机构收拢状态示意图。
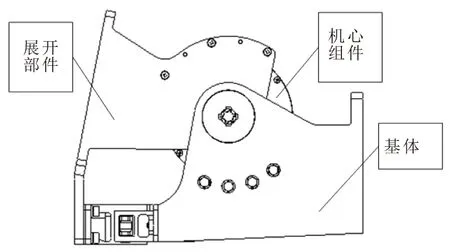
图1 无源展开机构展开状态示意Fig.1 Unfolding of passive unfolding mechanism
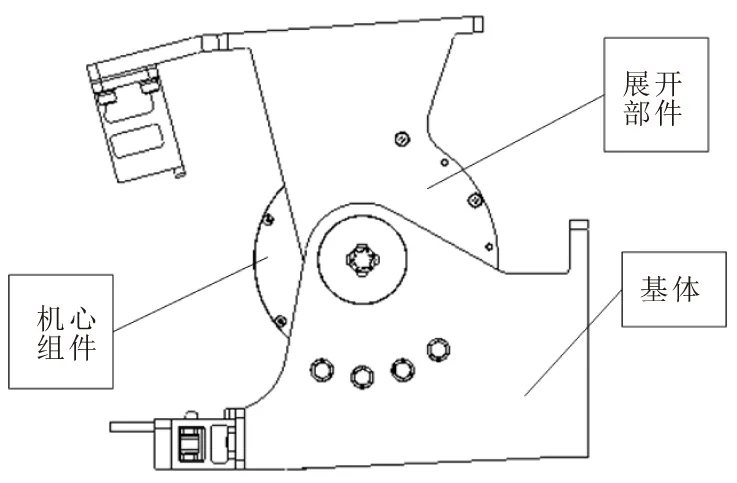
图2 无源展开机构收拢状态示意Fig.2 Closing of passive unfolding mechanism
无源展开机构具有支撑连接功能和展开驱动功能,是组成展开天线的重要部件之一,重量轻,且能够满足空间环境的使用要求。在空间环境条件下,无源展开机构应具有较大的驱动力矩、并能控速延时。本文结合展开机构功能要求,对相关设计技术进行了分析研究。
机心组件装在铰链架组件中,机心组件驱动铰链架组件展开,展开到位后锁定装置对铰链架组件进行锁定。发条是无源展开机构的动力源,无源展开机构收拢后通过上条工装给发条上条,使发条上紧、储备势能,当展开部件被释放后发条同时开始释放储备的能量,其中一部份能量通过增力驱动轮系传递至铰链架,驱动展开部件展开;另一部分能量通过控速延时轮系传递至擒纵机构,通过擒纵机构实现发条缓慢释放,如图3为无源展开机构工作原理框图[1]。
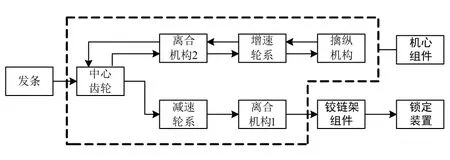
图3 无源展开机构工作原理框图Fig.3 Block diagram of the working principle of the passive deployment mechanism
1 可拆卸结构设计
机心组件设计为可拆卸式机构,同时拆卸后不影响铰链架组件及卫星天线肋的连接状态。机心地面研制试验阶段可拆卸维护,延长了产品的使用寿命,可提高展开机构的可靠性。在收拢状态下,卸除基体两侧的定位螺钉,即可拆除机心组件,不会造成展开部件位置精度变化,如图4为可拆卸示意。
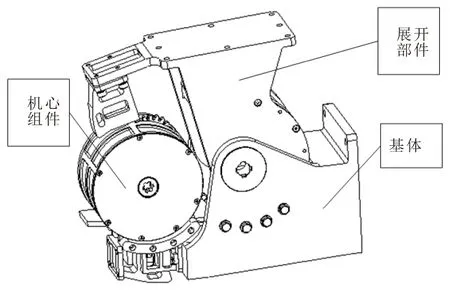
图4 可拆卸示意图Fig.4 Detachable indication
2 锁体入锁力矩分析
锁体在工作历程中,需要满足在相应的力学环境下,状态不发生改变的条件。在振动条件下,锁体组件应保持初始状态(见图5),所以在设计锁体组件时,需要使锁体组件的入锁阻力矩最小,又能满足抗振动环境的需要。结合随机振动的总均方根为14gRMS,其峰值加速度按经验估算为42g,进行插销弹簧和滑块弹簧的计算[2],并对入锁阻力矩进行计算。
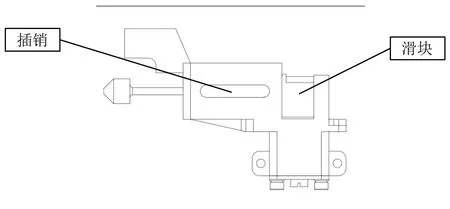
图5 锁体结构示意Fig.5 Lock body structure
2.1 锁体自动落锁力分析
滑块的质量为3.98×10-3kg
滑块导杆的质量为4.41×10-3kg
滑块与滑块导杆在峰值加速度下产生的冲击力为:
Ff=(3.95+4.41)×10-3×42×9.8=3.45N
2.2 插销弹簧分析
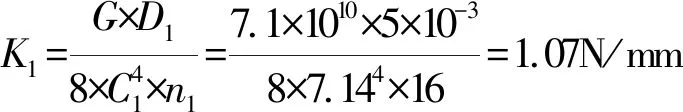
插销对滑块的正压力:
F1=K1×Δx1=1.07×(46-20.5)=27.29N
入锁过程需克服滑块与轨道的滑动摩擦力:
f=μ×F1=0.15×27.29=4.09N
2.3 滑块弹簧分析
弹簧刚度
入锁过程滑块弹簧对滑块的弹力:
F2=K2×Δx2=0.22×(46-22)=5.06N
由此得出滑块入锁最大阻力:
Fz=f+F2=4.09+5.06=9.15N
结合3.1章节计算的自动落锁力(Ff)小于滑块的入锁最大阻力(Fz),即在振动环境下不会产生自动落锁的现象。
2.4 入锁阻力矩的分析
无源展开机构入锁力作用半径:L=0.058m
无源展开机构入锁阻力矩:Mf2=Fz×L=0.53Nm
计算入所阻力矩相较驱动力矩在可接受的范围,设计值满足展开机构要求。
3 擒纵机构动力学仿真分析
无源展开机构机心采用擒纵机构来控制输出转速,擒纵机构由平衡摆和擒纵轮组成,发条的力矩通过轮系传递到擒纵轮,迫使擒纵轮与平衡摆之间产生周期性碰撞,以此来减缓系统能量的消耗,从而控制输出转速。通过Adams软件对擒纵机构进行动力学仿真分析,为机心设计提供数据支撑。
3.1 动力学模型建立
将建立好的平衡摆部件、擒纵轮部件和夹板导入Adams中,赋予各零部件相应的材料参数。根据运动原理建立约束关系:夹板相对大地的固定副,平衡摆与平衡摆轴固定副,擒纵轮与擒纵轮轴的固定副;平衡摆轴与夹板的转动副;擒纵轮轴与夹板的转动副[3,4]。建立好的约束关系如表1所示。
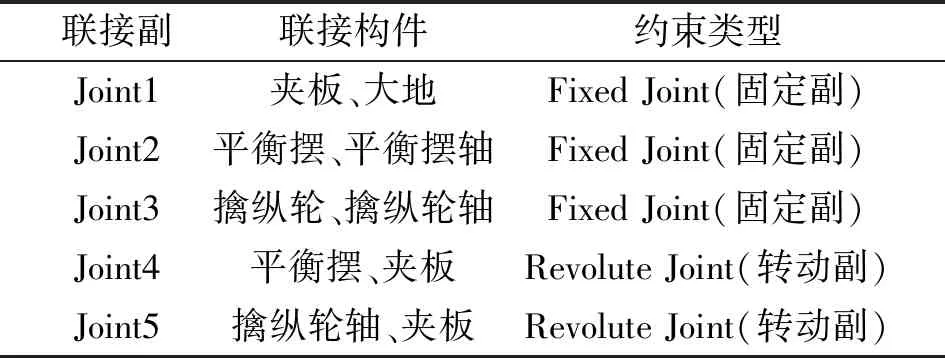
表1 索网单元张拉力分布值Tab.1 Constraint condition of Equivalent callision
擒纵轮与平衡摆之间的接触碰撞采用IMPACT函数,两个零件之间的碰撞力可以等效为非线性弹性力与非线性阻尼力的合成效果,其表达式为
(1)
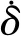
根据Hertz接触理论,平衡摆与骑马轮之间的接触刚度k可以表示为
(2)
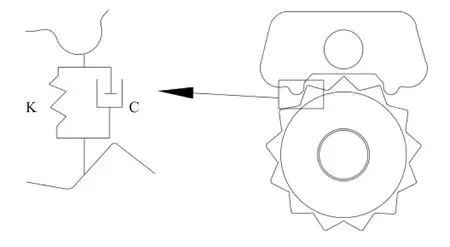
图6 擒纵机构等效碰撞示意图Fig.6 Schematic diagram of Equivalent collision
3.2 动力学仿真根据发条释放时的输出力矩分析,传递到擒纵轮的驱动力矩为1.0 N·mm~1.4N·mm。运用ADAMS仿真软件在擒纵轮上分别施加1.0N·mm、1.1 N·mm、1.2 N·mm、1.3N·mm、1.4N·mm、1.6 N·mm 、1.8 N·mm、2.0 N·mm 、2.2 N·mm 、2.4 N·mm 、2.6 N·mm和2.8N·mm驱动力矩[6],平衡摆转角与时间的关系曲线如图所示:
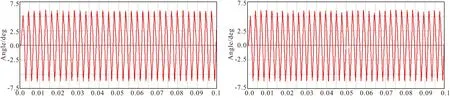
1.0N·mm驱动力矩 1.1 N·mm驱动力矩
3.3 动力学仿真结果分析
通过以上分析可以得出不同驱动力矩下平衡摆的振动周期与驱动力矩的关系,驱动力矩越大,平衡摆的振动周期越短。而发条在释放过程中力矩会发生变化,这将会对平衡摆振动周期带来影响,所以在设计过程中要给予特别关注。
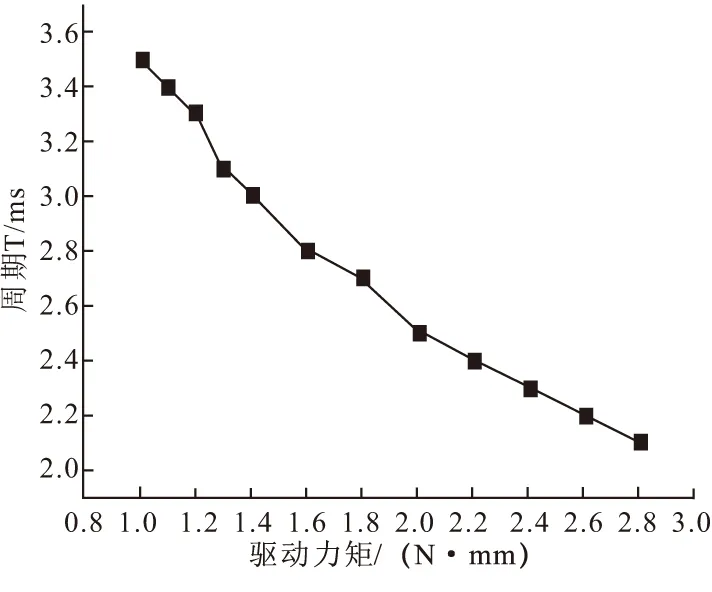
图8 驱动力矩与振动周期关系曲线Fig.8 Influence of driving torque on vibration period
4 结论
无源展开机构采用模块化的设计理念,并对机心拆卸结构、锁定装置阻力矩、擒纵机构振动周期等设计主要关注点进行了分析计算,可有效支撑展开机构的设计;采用可拆卸结构后,通过维护手段可大幅提高产品的可靠性。可拆卸机心无源展开机构机心组件可拆卸结构设计合理可行,提高了产品的维修性与互换性,缩短了卫星天线的安装调试周期,可满足未来天线高可靠性与短周期的需求。
