大型空间结构热致动态响应研究综述①

冯雨晴，马小飞，李 洋

(中国空间技术研究院西安分院，西安 710000)

0 引言

航天器上的空间桅杆、太阳翼以及天线等柔性附件由于具有尺寸大、质量轻、刚度小以及热容较小的特点，被统称为大型柔性空间结构(Large Flexible Space Structure，简称LFSS)。太空中的载荷环境极其恶劣，LFSS在轨运行时，不仅要长期承受失重、低温以及真空的影响，还会受到周围环境如太阳、行星以及自身设备的周期性加热冷却，尤其是在进出地球阴影区时会受到突变的太阳热流，导致其结构的受照面与非受照面温差可达200K以上。温差大以及温度的不均匀分布都会对LFSS产生影响，不均匀的温度分布会使得LFSS产生不均匀的热应变，从而产生不均匀的热应力，最终引发LFSS的热致结构响应(Thermally-Induced Structure Responses)，影响航天器在轨运行时的正常工作。

热致结构响应按照结构响应的不同情况，可以分为以下五种：热碾轧、热弹性冲击、热致变形、热致振动以及热颤振[1]。其中，热致振动与热颤振统称为热致结构动态响应(Thermally-Induced Structure Dynamic Responses)，这两者均是由于外界温度突变导致的振荡运动，该振荡运动是准静态变形与周期性振荡运动的叠加。而热致振动与热颤振的区别在于，前者是稳定的结构振动响应，后者是在特定条件下，结构振动与热载荷相互耦合引发的不稳定结构振动响应。

热致动态响应对航天器危害很大，一方面会影响结构自身的精度，另一方面该结构的振动频率可能会与其他附件产生共振，除此之外由于航天器角动量守恒，附件的热致动态响应也会影响航天器本体的姿态，严重时可能导致航天器的失效，例如1960年，OGO-IV卫星在昼夜交替时，附件梁产生了热致振动，导致任务失败；1990年发射的哈勃太空望远镜(HST)在进出地球阴影时，太阳翼发生了弯扭耦合的热致振动，导致成像畸变、图像质量下降[2]；同年10月6日发射的Ulysses宇宙飞船在太阳热流的加热下，7.5 m长的天线吊杆横截面内产生温度梯度，导致天线产生弯曲振动，由于角动量守恒，引起飞船本体的振动[3]。除此之外，Apollo 15、GGSE III-VI、Voyager等航天器在轨运行时，也均产生了热致动态响应。由此可见，对突变热流作用下的LFSS进行热致动态响应分析是十分必要的。

本文以LFSS为研究对象，结合空间轨道热环境的背景，简述了判断结构是否发生热致振动的关键参数：Boley系数，对空间柔性结构热致动态响应以及热颤振准则的研究进展进行了调研汇总与综述，并在此基础上，对未来研究发展的趋势进行了展望。

1 空间轨道热载荷分析

航天器在轨运行时，处于真空、低温与电磁辐射的环境中。在真空环境中，由于不存在气体，故不考虑对流换热，航天器与空间环境的热交换只考虑辐射换热与热传导。其次，宇宙空间的背景温度约为4 K，属于超低温，也被称为“低温热沉”。太阳以5777 K等效黑体以电磁辐射形式向外发射能量，达到地球附近的平均太阳辐射强度称为太阳常数，约为1367 W/m2。地球等效黑体温度约为250 K[4]。

空间结构在轨运行时受到的热载荷按照来源可以分为两种：从外界环境中吸收的热流以及航天器自身的产热。对于地球轨道航天器，从外界环境中吸收的热流是电磁辐射的热能，主要包括三个部分：太阳电磁辐射、地球反射的太阳辐射以及地球红外辐射。故热平衡方程为：

Q1+Q2+Q3+Q4-QR=Q5

(1)

上式中：Q1为太阳辐射热能；Q2为地球反射热能；Q3为地球红外热能；Q4为内热源热能；QR为航天器向外辐射热能；Q5为航天器内能的变化。

航天器在轨运行时，会周期性地经过光照区、半阴影区、阴影区以及半阴影区，如图1所示。在光照区，航天器可以直接受到太阳辐射的热流而不受地球的影响，然而对于空间结构而言，当其处于光照区，只有向阳的一面受太阳辐射，背阳的一面仍不受照射；在半阴影区，只能受到一部分太阳辐射的热流；而在阴影区，由于地球的遮挡，航天器无法受到太阳辐射热流。

图1 地球阴影区示意图Fig.1 Earth’s Shadow Region

图1中可以看出：经历半影区的时间长短主要是由轨道高度决定，对于低轨运行的航天器，经历的半影区时间较短，在进出地影时，热流加载与卸载速度较快；而对于高轨运行的航天器，经历的半影区时间较长，在进出地影时，热流加载与卸载的速度较慢。因此，不同轨道的航天器在进出地影时，热致动态响应是不同的。

2 Boley系数判定方法

1956年，Boley[5]从理论上研究单面受突加热流的简支矩形截面梁时，首次引入了惯性项，提出了空间结构热致振动的概念，并提出了无量纲Boley系数B。随后，1972年，Boley[6]又定义结构发生热致振动的无量纲参数B为热特征时间与结构特征时间的比值：

(2)

上式中：tT为结构的热特征时间(对于矩形截面梁，tT=h2/κ，h为梁的高度，κ为截面高度方向的导温系数)；tw为结构特征时间(正比于结构第一阶固有频率的倒数)。

Boley还提出了放大因子，用以近似计算温度突变引起的结构最大动态位移与最大准静态位移的比值：

(3)

上式中：wdyn为考虑了惯性项的结构最大动态位移；wst为最大准静态位移。

由式(3)可以看出：wdyn/wst<2，也就是说振动的振幅恒小于其准静态值；当B≫1时，wdyn≈wst，在分析突变热流作用下结构的热致响应时，可以不考虑惯性项，采用热致变形的分析方法即可；当B≪1时，wdyn≈2wst，此时不能忽略惯性项的影响，结构的热致动态响应应该为准静态变形与周期性振动的叠加。事实上，上述公式只对非耦合的热致振动近似成立，而在耦合分析中可能出现热颤振，wdyn/wst可能远大于2。

由于大多数航天器上柔性附件振动的模态与悬臂梁较为接近，故Boley系数也能够很好地反应航天器上柔性附件的热致振动情况。然而，最新试验表明，较大的Boley系数仍可能引起结构的热致振动[7]。

3 空间结构热致动态响应与热颤振准则研究进展

3.1 热致动态响应研究进展

3.1.1 国外研究进展

上世纪50年代之前，人们对热-结构关系的认识还只是简单的热致变形，从1956年Boley提出热致振动概念后，才引起人们的关注。

Boley[5，6]在研究梁与薄板的热致振动时，首次引入惯性项，将瞬态热弯矩代入其动力学方程中，从理论上提出了可用来判断结构是否会发生热致振动的无量纲Boley系数。

在Boley基础上，不断有学者对梁、板、壳的热致动态响应情况进行研究。Seibert和Rice[8]、Manolis和Beskos[9]等也都对梁的热致振动进行了理论分析，但导热方程中均不含有高度非线性的辐射换热项。Jones[10]考虑了剪切变形、转动惯量以及梁轴力，研究了Rayleigh梁和Timoshenko梁在简支条件下轴向与弯曲的热诱发振动。Kraus[11]对简支非浅球壳的热致振动情况进行了研究，并指出球壳得出了与梁、板完全不同的解，最大位移与准静态位移的稳定值没有同时达到。Ray与Lovell[12]研究了薄壁圆柱壳在轴对称突加热载荷作用下的结构响应。Tauchert[13]研究了具有两个平行简支边的正交各向异性板表面在快速加热载荷作用下的热致动态响应情况。Thornton与Foster[14]研究了热-结构非耦合时悬臂梁的热致动态响应，并指出热流密度越大，结构越不稳定。

以上学者都只是从理论上证明结构可能会发生热致振动，直到1968年，NASA观测到OGO-IV卫星在昼夜交替时，附件梁产生了热致振动，才证实了Boley理论。

同年，Beam[15]首次在实验室发现了开口悬臂梁不稳定的弯扭耦合热致振动现象，证实热颤振是存在的。该试验具有十分重要的意义，因为在此之前，学者们都只考虑稳定的热致振动情况。两个月后，Augusti[16，17]考虑了热-结构耦合，即认为结构变形后，热流的入射角会发生相应改变，如图2所示，首次从理论上证明了开口薄壁杆发生弯扭耦合热颤振是可能的。

(a)变形前(a)Orginal structure

自从1990年HST在进出地球阴影时，太阳翼发生弯扭耦合的热致振动，此后吸引了更多学者对此进行研究。Thornton与Kim[18]研究了HST太阳翼的左/右对称梁在热-结构非耦合与热-结构耦合状态下的热致振动情况。他们将截面内的温度拆分为平均温度 与摄动温度 两项：

(4)

并给出了相应的热颤振准则。他们指出：当不考虑热-结构耦合时，梁的热致振动是稳定的；考虑热-结构耦合时，梁可能发生热颤振。然而不足的是，他们只是从理论上研究了梁的弯曲振动，实际中太阳翼为弯扭耦合振动。Chung与Thornton[19]对HST的太阳翼进行了模态分析，研究表明其最低阶扭转频率0.027 Hz远小于最低阶弯曲频率0.097 Hz，根据式(2)可知，该太阳翼很容易被激发扭转形态的热致振动。Murozono与Thornton[20]对HST太阳毯中线偏离左/右梁中线55.5 mm的非对称左/右梁(图3)进行了屈曲以及准静态热-结构响应的分析。研究表明，太阳毯的一阶模态受扭转变形影响，二阶模态主要为弯曲，也包含较小的扭转变形分量，较高的模态则受到弯扭耦合的影响。该屈曲结果形式上符合其真实破坏情况，但是不足之处为研究中使用闭口薄壁杆近似代替实际的开口薄壁杆。

图3 HST太阳翼几何非对称模型Fig.3 Geometric Asymmetry Model of HST solar array

以上文献都是结构热致动态响应理论解，可以发现，以上理论解大多都是建立在简单梁的模型基础上，但是真实的空间结构是十分复杂的，单纯用理论解已经很难完成，除非做很多的简化，这时数值解就应运而生了。

Mason[21]首次将有限元法引入到结构的热致振动分析中。他以简支梁与简支板为模型，首先采用二维平面单元计算出随时间变化的温度梯度，然后将温度场分析得到的等效温度载荷作为节点力施加在结构上，从而求得结构的热致动态响应，并且把有限元方法计算出的结果与理论解进行比对，证明该方法具有可行性。Frisch[22]提出在对复杂结构计算热致动态响应时，可以采用商业软件进行分析，如NASTRAN、SBAR、SINDA、TRASYS、DISCOS等，但是使用时存在一定的条件，需要确保与时间无关的辐射系数保持恒定。Namburu与Tamma[23]使用有限元方法对受线性/非线性热效应和任意热载荷作用下的热致结构动态结构响应进行了分析，但他们使用了普通的三维单元计算，运算量较大，不适用于复杂结构。Givoli与Rand[24]发展了一种新的温度单元，他们将温度Fourier展开为平均温度与摄动温度，以此来进行结构温度场的计算，最重要的是这种方法可以使用同一套网格进行温度场与变形场的计算，大大减小了计算量，但是计算过程中平均温度与摄动温度没有解耦，计算效率不够高。Chen等[25]采用三维单元先求出结构温度场，随后将其等效为节点力作用在梁结构上，进而求得结构热致动态响应。但是他们在进行热分析与结构分析时采用的模型不相同，导致计算量较大，并且只适用于热-结构非耦合的情况。可以看出，该方法与Mason[21]方法较为相似，区别在于前者为三维单元，后者为二维单元。

基于上述基础，Azadi等[26]研究了太阳翼表面压电作动器不同位置以及输入电压对其热致振动的影响。Javani等[27]建立了一维瞬态Fourier导热方程，随后采用直接积分法得到了环形扇形板在突加热流作用下任一时刻的位移矢量。

3.1.2 国内研究进展

从2000年左右起，国内一些高校与科研机构才开始对空间结构的热致动态响应进行研究。虽然起步较晚，却取得了一定的成绩。

安翔[28]提出了边界耦合的概念，首次给出了空间悬臂梁完整的稳定性条件，并分析了影响悬臂梁稳定性的关键因素。

目前，清华大学薛明德课题组在该领域颇有建树，他们提出的Fourier温度有限元法可以使结构的温度单元与结构单元共用一套网格并且平均温度与摄动温度解耦，将热致动态响应由理论阶段加速进入了工程阶段。薛明徳与丁勇等[29]提出了一种可用来计算薄壁圆杆温度场的Fourier温度有限元法。沿杆轴向采用有限元离散，沿周向Fourier展开为三角函数：

T(s，ζ，t)≈T0(ζ，t)+

(5)

这样一来，圆管温度单元的每个节点有三个自由度：平均温度、余弦分布温度幅与正弦分布温度幅。且在每个时间步内，这三个自由度互相解耦，从而得到结构温度场。该方法相比商业软件，可以减少计算时间。不足的是只适用于闭口薄壁杆件，不适用于开口薄壁杆。姚海民等[30]在Fourier温度有限元基础上，求解了结构的动力学响应。程乐锦与薛明德[31]发展了一种热-动力学耦合的有限元方法，并研究了热颤振机理。李伟等[32，33]将Fourier温度管单元推广至任意截面形状的闭口薄壁管，并且对卫星刚体-结构附件耦合系统的热-动力学运动稳定性进行了分析。段进[34]将Fourier温度单元推广至单支开口薄壁管，并且考虑了梁单元大转动与截面翘曲的影响，发展了几何非线性热-结构耦合有限元方法。图4所示为HST左右梁开口方向相差20°且热流入射角为80°时，左右梁端部挠度响应图。可以看出，线性分析与非线性分析得出完全不同的结果，几何非线性会对其稳定性造成明显的影响。范立佳[35]基于前人热致振动的分析方法，发展了一种稳健性优化设计方法来解决LFSS热致响应的被动控制问题。上述研究成果均建立在“截面内温差引起热致动态响应”的理论之上，然而Shen等[36]指出对于复杂的环形桁架结构，热致振动很可能是由轴向温度梯度引起而非横截面内温差引起，却并未进一步分析论证。

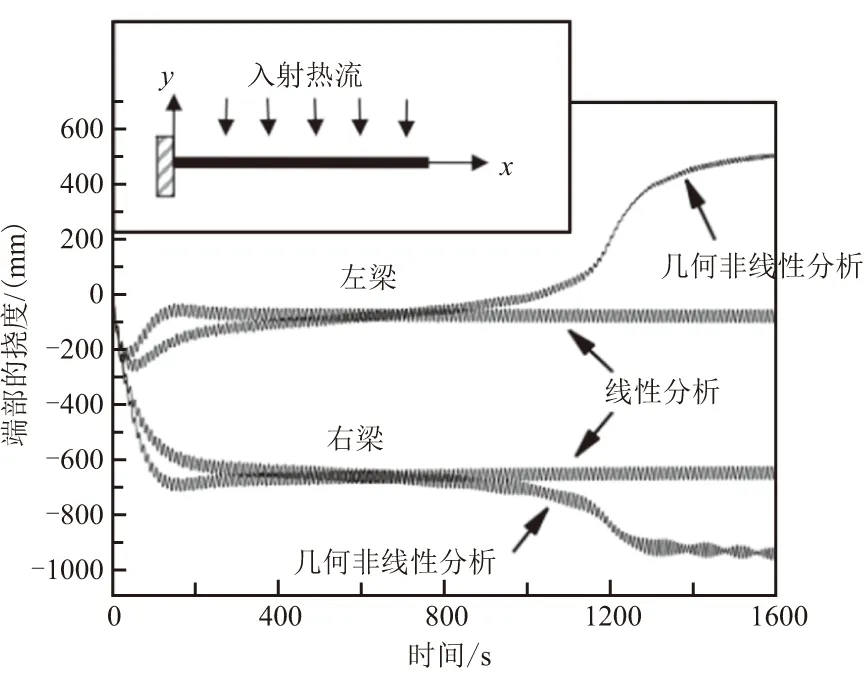
图4 线性与非线性端部挠度对比图Fig.4 Comparison of linear and nonlinear end deflection of beam

蒋卓良[37]对太阳能帆板的主梁进行了模态分析，研究表明当主梁的密度与弹性模量随温度升高而降低时，固有频率也相应地降低。张海涛[38]综合了天线吸收-发射比、约束方式以及阻尼三因素，采用正交试验法对多因素影响下的天线热振动进行了研究。Shen等[39]针对空间可展结构在展开过程中，热载荷对大位移、大旋转结构的影响，提出了一种基于绝对节点坐标系的耦合热效应梁模型。薛碧洁[40]对索梁结构的热振动进行了研究，她指出Boley系数不仅适用于线性系统热振动分析，也适用于索梁结构这种非线性系统的热振动分析。耿盛韦[41]对考虑几何刚度的柔性太阳翼热致动态响应进行了研究。他指出，柔性太阳翼属于大挠性空间结构，柔性阵面无刚框，需作用张紧力来维持阵面刚度，从而引起几何刚度。王祥[42]基于Fourier有限元方法，分析了口径为12.5m的环形桁架受突加太阳辐射时的热-结构响应。左亚帅与刘锦阳[43]以低轨运行的卫星-太阳能帆板为研究对象，提出了一种可以分析其在宇宙空间各种热流作用下刚-柔-热耦合动力学特性的建模方法。郑士昆等[44]将结构的应变看作弹性应变与热应变的线性叠加，得到环形桁架天线索网-框架组合结构的热-弹耦合动力学方程。Liu等[45]基于Hamilton原理，建立了航天器刚-柔耦合动力学模型，并对比了单、双太阳能帆板热致动态响应情况。当结构发生不受期待的热致振动时，便需要对此进行控制。Zhang等[46]通过在空间结构表面施加控制热流，改变结构内的温度梯度，使结构本身产生受控的热弯矩与热轴力，从而对其热致动态响应进行主动控制。何鹏[47]使用作动器并采用新型快速模型预测控制算法(NFMPC)对星载天线的热振动现象进行了主动控制。

可以看出，目前学者的研究大多集中在理论研究以及计算分析上，进行的相关试验非常少。Su等[7]首次在国内开展了热致动态响应的试验，这也是公开文献中第一个关于复杂结构的热致动态响应试验。他们基于薛明德课题组提出的Fourier有限元程序[29-35]，合理设计了空间桁架结构，如图5所示，并对其进行了11种不同工况下的热致动态响应试验。试验中观测到 与背景温度、热流密度以及真空度之间的关系与理论预测一致，并且测得的结构振动频率与理论计算结果一致，验证了理论模型与Fourier有限元方法的正确性。Fan等[48]通过对一端固支的细长薄壁管加载与卸载热流，来模拟空间结构进入与离开地影区时的热致振动现象。综上所述，热致动态响应的研究大体经过了三个阶段：理论解-数值解-试验。

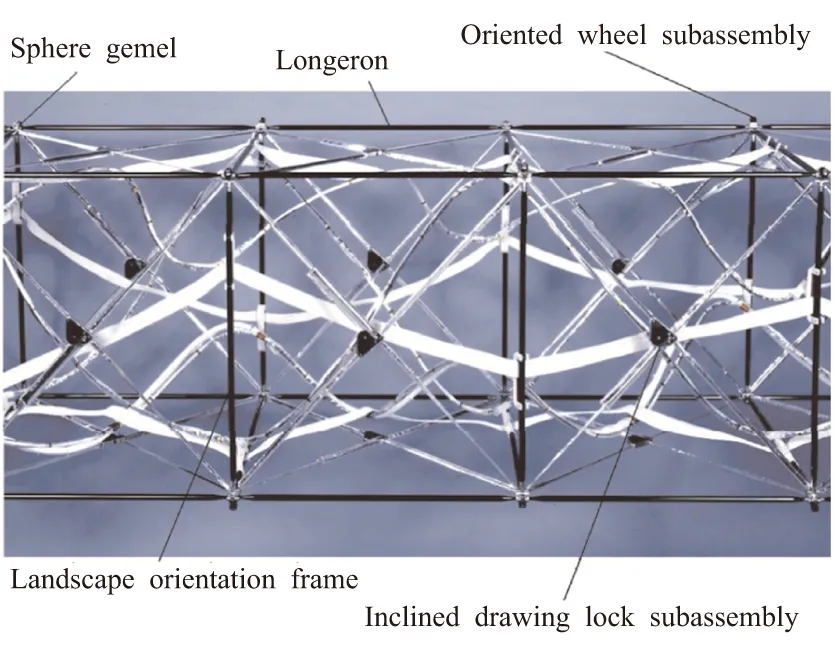
图5 空间桁架外观Fig.5 Appearance of space truss

3.2 热颤振准则研究进展

从物理上来说，热致振动的稳定性源于热-结构耦合的影响，其原理为：结构的变形改变了热流入射角，从而改变结构温度，进而影响等效热载荷(包括热轴力、热弯矩和热双力矩等)，使结构产生了载荷增量。若该载荷增量与速度方向一致，则会加剧结构振动，振动是不稳定的即产生热颤振，反之，振动是稳定的[34]。

Yu[49]以不考虑扭转、只考虑弯曲振动并带有末端质量的悬臂梁为模型，得到了热颤振准则。然而，Graham[50]指出Yu[49]对边界条件的近似产生了错误的准则，并得到了与Yu[49]完全相反的悬臂梁热颤振准则：当悬臂梁从固定端指向自由端的轴线指向太阳时，结构产生稳定的热致振动；而当轴线背离太阳时，结构产生热颤振。Thornton与Kim[18]给出了HST太阳翼发生热颤振的准则，他们肯定了Graham[50]的理论，同时又提出从固定端指向自由端的轴线与太阳垂直时，结构产生稳定的热致振动。然而，Rimrott与Abdel-Sayed[51]在实验室中发现了一个与上述准则矛盾的现象：当热流垂直入射时，悬臂梁发生热颤振。李伟等[32]针对大型空间结构耦合非线性振动问题，提出了稳定准则的确定方法，并对比了热流入射角以及阻尼比对系统稳定性的影响。张军徽[52]指出Graham与Thornton提出的热颤振准则是错误的，因为他们在分析非线性系统的稳定性时，没有在系统稳定状态附近分析，却错误地在初始状态附近分析，错误地应用了Lyapunov稳定性第一方法。随后，他得到了空间热流作用下悬臂梁新的热颤振准则：悬臂梁结构不发生热颤振的条件为，空间热流的入射角大于在该入射角下稳定状态时梁自由端的准静态转角。Yuan与Xiang[53]研究了开口悬臂梁的稳定性准则。值得注意的是，他们指出在不考虑阻尼时，即使开口悬臂梁初始只发生纯弯曲振动，后期也可能出现扭转失稳，如图6所示。

(a)开口薄壁圆形悬臂梁受突加热流(a)open beam exposed to solar heat flux

以上热颤振准则都是针对单独附件而言，但真实航天器上的柔性附件与舱体之间是具有耦合效应的，樊孝清[54]从理论上推导出带有柔性附件的航天器热颤振准则，并讨论了热流入射角、舱体质量特性、设备特性以及阻尼比对热颤振的影响，但不足之处为没有考虑沿梁轴向的导热。

4 未来研究发展趋势

因此，针对大型空间结构热致动态响应，未来研究趋势可能有：

(1)学者对于悬臂梁热致动态响应的研究是很多的，但是对于板、壳结构的研究较少，主要是因为板、壳结构相对于梁结构较复杂，但航天器上的板、壳结构也面临热致动态响应情况，故在此方面需进一步深入；

(2)以往学者在进行热致动态响应的基础理论研究时，均以单根悬臂梁作为研究对象，故认为结构横截面内存在温差时才会引起热振动，但对空间组合细长杆-梁结构而言，忽略截面内温差的情况是否也会引起热致动态响应尚无学者进行研究，可以对此进行进一步分析；

(3)对于复杂结构而言，实际中还存在着部件之间的遮挡效应，影响结构温度的分布，但目前对此方面研究的几乎没有，还需进一步研究；

(4)前人对航天器上单独附件的热致动态响应研究较多，而对于航天器舱体-附件耦合热致振动的研究较少。然而由于角动量守恒，附件的振动势必会引起航天器舱体姿态的变化，这是未来需要着重考虑的；

(5)几何刚度对柔性体(如太阳翼上柔性阵面)的固有模态影响较大，未来在对柔性体进行热致动态响应分析时，需要考虑几何刚度的影响；

(6)目前针对复杂结构的研究中，大多没有考虑结构与结构之间的连接情况，例如结构与结构、结构与舱体之间多为铰链连接，铰链之间的空隙可能会对热阻产生较大影响，需要进一步研究；

(7)目前，针对柔性结构的热致动态响应研究还停留在理论研究方面，国内外相关的试验较少。但是理论计算与数值模拟终究需要试验来验证，在地面模拟真实的太空环境(失重、低温、真空等)需要在真空罐中进行试验，除此之外，真实结构由于尺寸过大，无法放入有限体积真空罐中，故使用局部等效整体(模拟全尺寸结构的频率、刚度以及转动惯量等)进行试验是未来的发展趋势。

5 总结

过去的几十年间，在进行航天器发射时，大型的空间结构已经多被折叠成为体积较小的结构，例如可展开太阳能帆板以及可展开天线等，并且未来这些结构将向着尺寸更大、质量更轻的方向发展。这将不可避免地导致大型空间结构刚度越来越小，当这些结构进出地球阴影时，可能在突变热流作用下产生稳定的热致振动或不稳定的热颤振。文中综述了目前国内外学者对热致动态响应研究的最新进展，同时也指出了该领域尚未解决的问题以及未来的发展趋势，包括组件间相互作用对结构热致振动的影响、遮挡效应研究、舱体-附件耦合研究、几何刚度研究、铰链连接研究以及相关试验等。相信对该领域的研究未来一定具有重要的意义。