基于支持向量机的蠕墨铸铁表面粗糙度预测

鲁娟，张振坤，吴智强，马俊燕，廖小平，胡珊珊

（1.北部湾大学 机械与船舶海洋工程学院，广西 钦州 535011；2.广西大学 机械工程学院，南宁 530004；3.广西制造系统与先进制造技术重点实验室，南宁 530004）

蠕墨铸铁（CGI）是一种具有较好力学性能和导热性能的新型工程结构材料，是汽车发动机提高性能的理想材料，但它属于难加工材料，加工性能较差。蠕墨铸铁为铁素体结构，相比灰铸铁，其热导率较低，且在铸造过程中加入了蠕化剂和钛，这些都会加快加工过程中刀具的磨损[1]。为了改善蠕墨铸铁的加工性能，当前国内外，主要在切削温度、刀具磨损、合金和蠕化剂的添加等方面进行了研究[2-6]，对加工表面质量的关注相对偏少。随着工业4.0时代的到来，对汽车发动机的性能（如疲劳强度、耐腐蚀性、寿命和可靠性）提出了更高的要求。产品性能很大程度上由加工过程获得的产品质量决定[7]，而对产品质量而言，在加工过程中又受众多加工因素的影响，加之蠕墨铸铁的难加工性，使得在批量化加工过程中保证加工质量的稳定性成为蠕墨铸铁规模化应用的一个难题。

随着智能切削技术的发展，借助机器学习技术建立加工过程中对加工质量的预测模型，准确预测质量趋势，挖掘加工参数与加工质量之间的相关关系，从而有效指导加工参数的选择和调整，来保证加工质量的稳定，是促进加工材料规模化应用有效且低成本的方式[7-8]。在上述方式实现中，寻求满意的加工质量预测模型是保证后期调控的有效前提。表征产品质量的特征有很多，其中最主要的衡量特征是表面粗糙度，对加工质量的研究也主要集中在表面粗糙度。由于切削加工过程是一个复杂的过程，加工过程中各变量的变化很难用具体的数学模型来表达[7]。因此，基于数据的经验建模方法被广泛应用在表面粗糙度的建模中，如响应曲面法[9]、神经网络[10-11]、支持向量机（SVM）等[12-13]。SVM 是一种监督式的机器学习方法，依据结构风险最小化准则构建，故相比基于经验最小化准则构建的神经网络而言，它能减少模型过拟合的概率，而且结构中的不敏感区能吸收随机型响应中出现的小规模随机波动，故在切削加工过程预测中的应用较多[13-15]。余剑武等[13]针对电火花（EDM）加工过程，采用遗传算法优化支持向量机的内部参数（惩罚系数C、损失系数ε和核函数标准差σ），通过SVM 模型建立了脉冲开启、脉冲准备时间及电流与表面粗糙度的预测模型，并验证了构建预测模型的有效性。王兴盛等[14]研究了镜片车削加工过程表面粗糙度的变化，对比了回归分析和最小二乘支持向量机（LS-SVM）形成的表面粗糙度预测模型的精度，并用网格搜索和交叉验证获得 LS-SVM 模型的内部参数。基于实验数据建模，LS-SVM 模型的相关系数R2高达0.998 85，证明了LS-SVM模型优于回归分析模型。Aich等[15]采用SVM建立了电火花工艺的表面粗糙度参数预测模型，采用粒子群优化算法（PSO）优化SVM参数（C、ε、σ）。

合适的支持向量机内部参数能有效提高预测模型的精度，采用优化算法优化支持向量机内部参数可以确定最佳参数及有效减少参数调整时间，是确定支持向量机内部参数常用的方法。差分进化算法（Differential Evolution Algorithm，DE）是一种启发式全局搜索算法，具有寻优原理简单、寻优过程所需控制参数少、优化性能良好等优点，在很多方面已经取得了成功的应用[16-18]。到目前为止，关于差分进化算法在表面粗糙度预测模型的内部参数优化方面鲜有研究。因此，为提高加工过程表面粗糙度的预测精度，本文提出采用差分进化算法优化支持向量机预测模型的内部参数，构建表面粗糙度预测模型，并挖掘加工参数与表面粗糙度之间的关系，以有效指导参数调整，保证蠕墨铸铁批量化加工过程质量的优良，促进其高质量的规模化应用。

1 支持向量机回归

针对切削加工过程的复杂性和随机波动性以及实验数据的高成本，采用在小样本、非线性问题的拟合上有一定优势的支持向量机方法来构建蠕墨铸铁切削过程的表面粗糙度预测模型。

在切削加工中，把每一组实验的输入变量xi和输出变量（表面粗糙度）Rai，构成样本空间{(xi,Rai),i=1,2,3,…,n}。Rai可表示为如式（1）所示的非线性函数模型：

式中：φ(x)为输入空间x的非线性映射；ω为φ(x)的线性组合；b为偏置。此外，还应尽量减少训练误差的经验风险[17]。因此，ω和b可通过如式（2）所示的模型进行评估：

式中：C和L分别定义为惩罚因子和损失函数，C值表示对超出L的数据的惩罚程度。

随后引入ε-不敏感损失函数对结构风险最小化进行估计，ξi、ξi*定义为松弛变量，优化目标可变化为如下形式：

引入Lagrange方程：

SVM模型中的惩罚参数C权衡模型的复杂度和逼近误差的程度，其值的大小影响着模型学习能力。损失函数的参数ε控制回归函数对数据样本不敏感区域的宽度，设置过小，回归精度较高，但容易导致低的泛化能力；设置过大，获得的模型会过于简单，影响算法的学习精度。RBF核函数参数σ（核的宽度），关系着函数的径向作用范围。由此可见，SVM 的内部参数（C、ε、σ）值的选取决定着模型的预测性能。DE算法是一种高效的全局优化算法，可有效地为SVM 模型选择最佳的内部参数组合，提高模型的预测精度和泛化能力。

2 支持向量机预测建模

为了直观阐述基于差分进化算法优化参数的支持向量机表面粗糙度模型，结合具体的实验验证来描述。

2.1 实验

本实验中铣削加工的机床为 VDL-600A（大连机床）数控加工中心，最大主轴转速为8000 r/min，三轴行程为 620/420/520 mm，加工工件为蠕墨铸铁RuT400，工件尺寸为50 mm×50 mm×80 mm。基于学者对蠕墨铸铁加工刀具的研究，发现在蠕墨铸铁发动机缸体工作面精加工铣削工况下，就刀具寿命而言，铣削蠕墨铸铁时，选取涂层硬质合金刀具比选取陶瓷刀具更好[2]。因此本实验选用的面铣刀是 SANDVIK的直径为80 mm的刀片，刀杆型号为BGP-800-FMB27，刀片型号为APMT 1604 PDER DP5320(R0.8)，涂层为Teguco的超硬亚微米矩阵CVD涂层。

在加工过程中，加工的表面粗糙度受很多因素的影响。这些影响因素主要可以分为四类：加工参数、加工刀具属性、工件属性及切削环境[19]。当明确了加工对象和加工要求时，其加工工件就确定了，在加工过程中不会改变，切削刀具也只能在车间可用的刀具中选择，而操作人员也不能控制切削环境（如切削力、振动等）[20]，因而加工刀具、工件及环境因素不容易调整改变或控制。加工参数在加工过程中往往是容易控制和调节的，为了获取好的加工质量，在加工初期，加工参数可以择优选择。在加工过程中，也可以调整加工参数，以保持加工质量的稳定。在铣削加工过程中，切削速度（v）、进给速度（vf）和切削深度（ap）为影响表面粗糙度最主要的加工参数。因此本文选择它们作为影响因素，以蠕墨铸铁RuT400加工后的表面粗糙度为目标，对三个加工参数选取不同水平值，设计了60组实验，采用Mitutoyo Surftest SJ-310表面粗糙度仪测量粗糙度值。实验参数及因素水平见表1。在60组加工参数不同组合及对应的表面粗糙度数据中，选取前50组作为预测模型的训练集，后10组为预测模型的测试集。

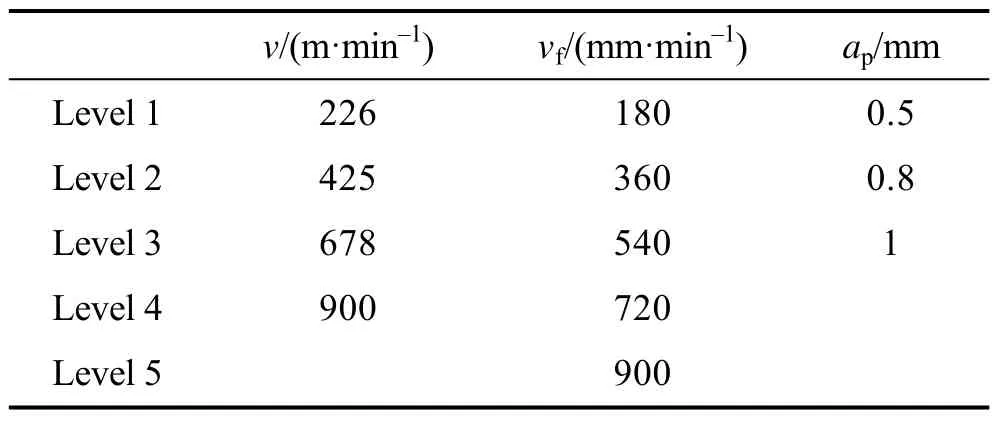
表1 输入参数及水平Tab.1 Input parameters and levels

2.2 内部参数优化的支持向量机回归模型

为获得满意的支持向量机内部参数，采用DE算法对参数C、ε、σ进行优化。DE的寻优过程主要包括变异、交叉和选择三个操作。内部参数优化的支持向量机预测模型具体建模包含优化参数的范围确定、适应度函数的选择以及算法流程三个部分。

2.2.1 优化参数的范围确定

在寻优的过程中，较大的参数范围会产生较好的搜索空间，往往会得到较好的参数组合，但会花费较多的搜索时间。为了减少搜索时间，本文对三个优化参数的搜索范围进行计算，确定其有效的搜索空间。对于参数C，首先通过Cherkassky等[21]和Levis等[22]提出的基于目标值的表达式得到C的估计值。然后，再以计算的C值和目标变量平均值的 50%作为标准偏差均值的正态分布，在估计C值的两侧选择两个点来确定C的范围[10]，见式（10）。

式中：ybar、tσ是目标变量的标准偏差和均值。通过式(10)计算得到的C值为6.1155，其范围见表2。ε和σ的范围通过文献[20,23]确定，其具体表达式如式(11)和(12)所示，计算结果见表2。

式中：Z表示实验过程中影响最大的参数个数，对于文中蠕墨铸铁的铣削实验，Z=3，即切削速度、进给速度和切削深度。

表2 支持向量机的参数范围Tab.2 Parameter range of support vector machine

2.2.2 适应度函数的选择

考虑SVM能降低模型泛化误差的可能性，本文选取均方误差（MSE）作为适应度函数，即估计模型输出的最小化MSE为优化C、ε和σ的目标，如式（13）所示。

2.2.3 DE-SVM预测表面粗糙度流程

采用DE-SVM模型对50组训练集进行训练，迭代获得满足适应度函数（MSE最小）要求的C、ε、σ值组合。当超过预定义的最大迭代次数M，寻优结束。其搜索获得最佳内部参数过程如下：

首先定义一个大小为NP的种群，其中Xi是第i个个体，j表示第j维，D=3，xi,1、xi,2和xi,3分别对应 Ci、εi和σi，按式（14）对种群中的个体进行随机的初始化。

然后随机选择两个个体（个体互不相同），将选中的个体向量差进行缩放后，再与待变异个体合成向量，完成变异过程，如式（15）所示。

式中：r1、r2为[1,NP]区间内互不相等且不等于i的随机数；F表征缩放因子，且为常数；g表示种群变化过程中的第g代。

再在变异得到的个体子代与对应的父代之间按式（16）进行个体的随机选择，实现个体的交叉。

式中：CR称为交叉概率。

最后，基于贪婪算法，对比个体的MSE值，选择具有较小MSE的个体作为新的个体，如式（17）所示。

遍历种群中NP个个体，循环执行上述的变异、交叉和选择的操作，完成第一次迭代。然后继续迭代至M次，得到产生最小MSE值对应的C、ε和σ值，把对应的C、ε和σ值代入到SVM预测模型中，对10组测试集进行预测。DE-SVM构建的表面粗糙度预测模型的流程如图1所示。

3 结果分析

文中的优化算法（DE、GA和PSO）均为各算法的标准版本，其公共参数种群数量NP及最大迭代次数M分别设置为 100和 20，参数的优化范围均为表2所示的范围。每个优化算法的其他特定参数如下：

1）PSO设置。认知因子（c1）和社会因子（c2）分别代表个体和种群经验的权重，在本文中均设置为1.8。惯性权重控制粒子的先前速度会影响下一次迭代中的速度，其值为0.6。

2）GA设置。在本实验中，使用二进制编码的标准GA，交叉形式为单点交叉，交叉率设定为0.8，突变率为0.01，代沟值为0.8。

3）DE设置。缩放因子F影响两个解之间的差异波动，设置其值为 0.8，交叉率 CR决定了种群多样性的波动，其值设定为0.9。

为了能够定量地评价模型的预测性能，设置了3个评价指标，分别为平均绝对百分比误差（MAPE）、相关系数（R2）和运行时间（t），见式（18）和式（19）。

MAPE能有效评价数据间的波动性，R2表示所解释的变化与总变化的比例，是衡量已建立模型有效性的指标之一，运行时间能较好地体现模型复杂度。其中MAPE和t的值越小，R2值越大，说明模型的预测性能越好。

3.1 预测性能分析

从实验中随机选取10组数据作为模型的测试数据，用DE-SVM、GA-SVM和PSO-SVM分别对所建立的蠕墨铸铁的表面粗糙度预测模型进行测试。各模型得到的最优参数C、ε和σ组合见表3。三个模型获得的预测曲线如图2所示，其对应的评价指标见表4，10组测试数据的预测值和对应的相对误差见表5。

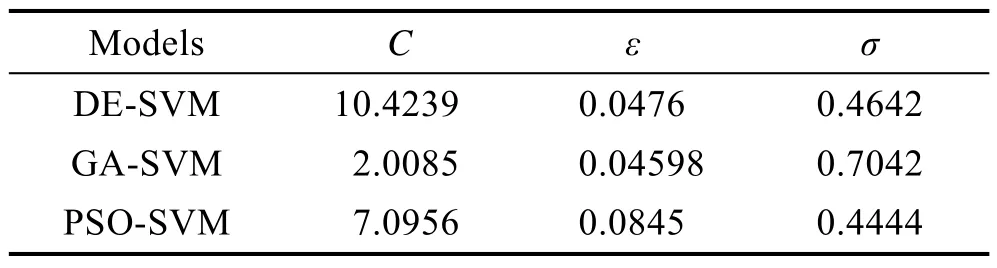
表3 预测模型的C、ε和σ值Tab.3 C, ε and σ values of the prediction model

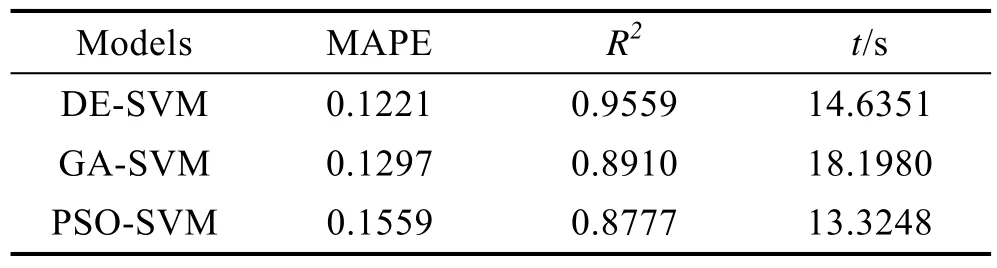
表4 各模型的评价指标值Tab.4 Evaluation index values of each model

从图2可以看出，DE-SVM、GA-SVM和PSO-SVM都能较好地捕捉到符合实际测量的趋势。其中，DESVM 模型获得的预测曲线与实际曲线更接近，而GA-SVM和PSO-SVM两者效果相近。由图2曲线可知，DE-SVM模型对10组测试数据中的1—6和9—10组的拟合效果要明显优于GA-SVM和PSO-SVM，而对7—8组的拟合效果不如GA-SVM和PSO-SVM。其主要原因是DE优化的支持向量机仅在概率上增大获得全局最优的可能性，从而使整体的预测精度提高，但并不使测试集中每个样本的精度都最高，因而有的样本没有取得最优值时，就会产生较大的误差，导致较低的预测精度。

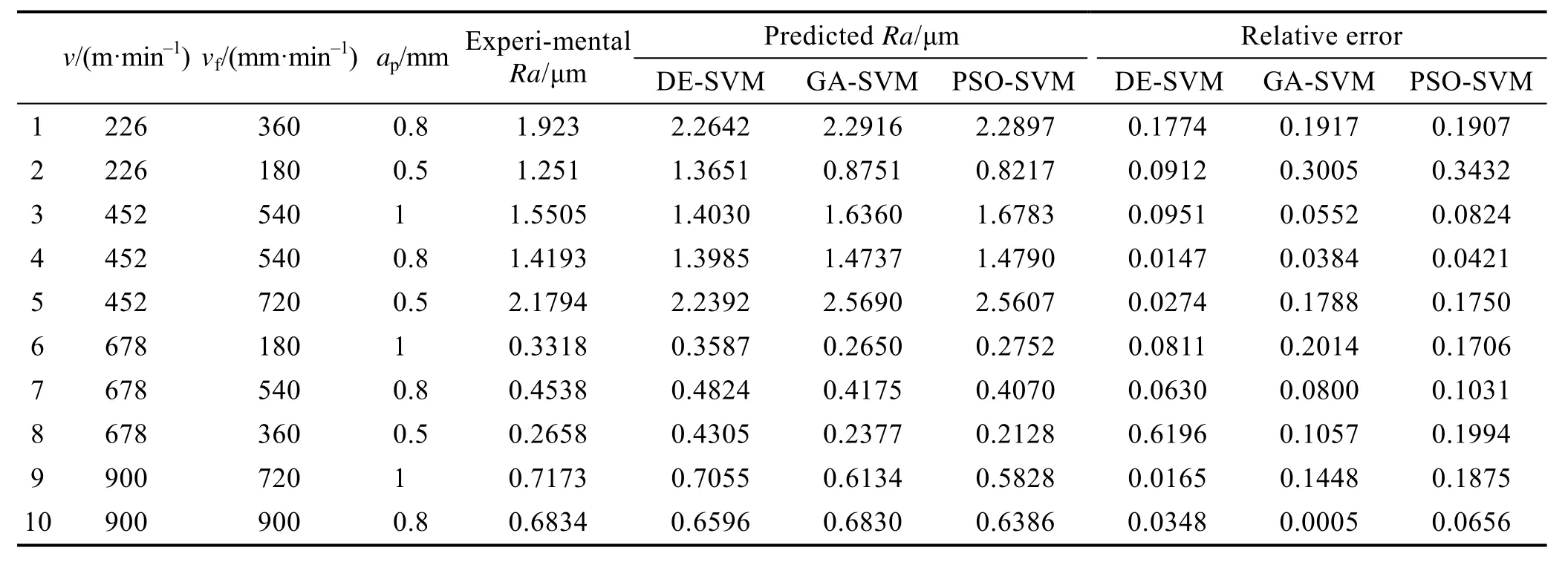
表5 各预测模型的预测结果与对应的相对误差Tab.5 Prediction result of each prediction model and corresponding relative error

基于表4的数据对比可知，DE-SVM 得到的MAPE和R2值最小，表示在三个模型中，DE-SVM具有最高的预测精度。另外从表5也可以看出，10个预测值对应的相对误差中，DE-SVM模型有7组实验的相对误差同时小于 GA-SVM 和 PSO-SVM。而DE-SVM的运行时间仅次于PSO-SVM，且两者相差不大。

因此，综合来看，相比粒子群算法和遗传算法，在蠕墨铸铁的表面粗糙度预测上，用差分进化算法优化支持向量能得到更好的预测效果。

从图2预测曲线可以直观看出，预测的10组数据中，1—5组加工参数获得的粗糙度值偏高，而 6—10组数据的粗糙度值较小。因此在实际加工过程中，可优先选择粗糙度值低的6、7、8组加工参数进行加工。这些加工参数组合与对应粗糙度值为选择切削加工参数和加工质量稳定的参数调控提供了依据。

3.2 加工参数与表面粗糙度的相关关系分析

DE-SVM 模型对蠕墨铸铁铣削加工的表面粗糙度的精确预测，可以预先判断加工零件的表面粗糙度值是否符合实际生产的要求，同时也可以得到正确的加工参数与表面粗糙度之间的关系。在实际加工过程中，可通过预测的表面粗糙度值及与加工参数的相关关系，逆向追溯加工参数，进行加工参数的优化，改进零件的表面粗糙度，保持加工过程质量的稳定。

基于蠕墨铸铁铣削加工的 DE-SVM模型，建立了选取的加工参数与表面粗糙度的关系图。当切削深度固定时，进给速度和切削速度对表面粗糙度的影响如图3所示。从图3可以看出，切削速度与进给速度对表面粗糙度有较大的影响，切削速度越大，表面粗糙度越小，表面粗糙度随着进给速度的增大而增大。切削速度固定时，切削深度与进给速度与表面粗糙度的关系如图4所示。进给速度固定时，切削深度与切削速度对表面粗糙度的影响如图5所示。从图4和图5可知，切削深度在选取的范围内改变时，表面粗糙度的变化很小，说明在给定的参数范围内，切削深度对表面粗糙度的影响不显著。基于关系图的这些结论，结合表5的实验数据进一步具体阐述，实验的6、7、8组加工参数组合中选择的切削速度（678 m/min）较高，且进给速度（180、540、360 mm/min）选取得不大，故加工得到的表面粗糙度值Ra（0.3318、0.4538、0.2568 μm）也相对较小。9、10两组的切削速度最高（900 m/min），但得到的Ra（0.7173、0.6834 μm）却高于6、7、8 组。这主要是由于进给速度（720、900 mm/min）设置较大，且进给速度与表面粗糙度正相关导致的。3、4组的切削速度（452 m/min）和进给速度（540 mm/min）都相同，但切削深度不同（0.8、0.5 mm）。由于切削深度对表面粗糙度影响较小，故获得的表面粗糙度值（1.5505、1.4195 μm）较相近。

从加工参数与表面粗糙度的相关关系分析可知，选取较高的切削速度与较低的进给速度以及合适范围内的切削深度，可以在蠕墨铸铁的铣削加工中获得良好的表面粗糙度，如预测数据中的6、7、8的参数组合。在实际选择中，可以选择多目标与加工参数的相关关系综合分析，基于给定的目标任务来实现智能化的参数选择，其加工参数选择的过程与单一目标下的相似，即通过相应的预测模型，获得各目标与加工参数的相关关系，再基于相关关系的综合分析，选择满足给定要求的加工参数。

4 结论

1）基于蠕墨铸铁的难加工性、铣削加工的随机波动性及加工过程的复杂性，选取支持向量机回归构建了铣削加工的蠕墨铸铁表面粗糙度预测模型，对蠕墨铸铁的加工过程研究具有一定的参考价值。

2）选取差分进化算法（DE）优化支持向量机模型的内部参数，并形成DE-SVM模型。采用DE-SVM模型构建了蠕墨铸铁铣削加工过程的表面粗糙度预测模型，并与常用的支持向量优化算法构建的预测模型（GA-SVM和PSO-SVM）进行了对比。展示了DESVM模型的高效性，同时也验证了相对GA和PSO优化算法，DE算法具有控制参数少、操作简单及寻优能力强的优点。

3）在DE-SVM模型构建的有效的表面粗糙度预测模型基础上，进一步挖掘了加工参数对表面粗糙度的影响，构建了影响参数与目标变量的相关关系图，可实现表面粗糙度的逆向追溯，对选择加工参数，改进加工过程，提高蠕墨铸铁铣削加工的表面质量，提供指导意义。