基于神经网络遗传算法的磁粒研磨TC4材料工艺参数优化

赵传营，赵玉刚，刘宁，宋盼盼，高跃武，张勇，刘广新

（山东理工大学 机械工程学院，山东 淄博 255000）

钛合金相对于传统的金属材料，具有比强度高、耐热耐腐蚀性好等特点，国内外已广泛应用于军事、航空航天、海洋船舶等领域。同时，钛合金质量轻、生物相容性好，在民生领域也得到较为广泛的应用，例如高尔夫球杆、人体体内植入物等[1-2]。但是，由于钛合金导热系数较低、弹性模量较低等特点，导致其可加工性能较差[3]。磁粒研磨光整加工是由永磁铁或电磁铁产生的磁场吸附磁性磨料除去被加工工件表面多余的金属，使工件获得高的表面质量的加工方式[4]，该加工方式具有温升小、自适应性好等特点。磁粒光整加工技术已经在各类金属及非金属材料的平面光整加工中得到应用，并取得了良好的效果[5]。

影响磁粒研磨光整加工的工艺参数很多，例如磨料粒径、主轴转速、加工间隙、加工介质、进给速率、磨料填充质量等。表面粗糙度通常作为检验磁粒研磨光整加工质量的重要指标，为了获得更优的工艺参数来降低工件表面粗糙度，想要通过数学公式表达各个工艺参数与表面粗糙度之间的复杂非线性关系是非常困难的。现通常采用正交试验对工艺参数进行优化，但是这种方法得到的优化结果只能来自于设定好的水平中，具有一定的局限性。BP神经网络是人工神经网络的类型之一，其模仿生物神经元的生理机能，能够进行大规模并行处理，具有容错性好、自适应和自组织能力强等特点，能够对复杂的非线性关系进行拟合[6]。遗传算法是根据自然界优胜劣汰的进化理论演化过来的随机性的全局优化方法，其能够直接操作结构对象，具有良好的全局寻优能力[7]。将 BP神经网络和遗传算法结合起来，可以避免二者单独使用的缺点，使建立的模型与实际工程更加吻合。

根据正交试验得到的数据组对BP神经网络进行训练，建立主轴转速n、加工间隙δ、进给速率v和磨料粒径D四个工艺参数与表面粗糙度Ra之间的对应关系，利用遗传算法良好的全局寻优能力对工艺参数进行优化。

1 试验

1.1 材料及设备

TC4钛合金作为α+β两相钛合金的一种，由于其耐高温性好、强度高、生物相容性好和易于成形的特点，在军事和民生领域得到了广泛应用，其产量占据钛合金总产量的一半[8]，因此TC4材料的表面光整加工问题亟待被解决。

本次试验选择一块长宽高为32 mm×20 mm×5 mm的TC4钛合金块作为被加工工件。基于XK7136C型，主轴被改造为磁极装夹装置的数控铣床作为磁粒研磨光整加工平台[9]。磁极采用底面开有六条槽宽和深度为2 mm的矩形槽，材料为Nd-Fe-B的N35型永磁铁，加工间隙为1.5～2.5 mm时，磁极产生的磁感应强度为0.35～0.5 T。使用双级雾化快凝法制备的磨粒相为金刚石的磁性磨料[10]，该方法使磨粒相与铁基相紧密结合，且磨粒相具有锋利的切削刃，制得的磨料球形度好，具有良好的微刃等高性能[11]，其SEM图如图1所示。使用型号为时代TR200的手持式表面粗糙度仪，测量加工后工件的表面粗糙度。

1.2 试验参数

正交试验可以在尽量减少试验次数的情况下进行一定程度的试验参数与试验结果之间关系的探究。磁粒研磨光整加工过程中有众多工艺参数，如主轴转速、加工间隙、进给速率、磨料粒径、磨料填充质量、工作介质等，其中磨料填充质量和工作介质对磁粒研磨结果的影响较小，将这两个因素作为常量处理，每组试验使用精密天平称取2 g金刚石磁性磨料和0.2 g SAE15W-40润滑油分别作为磨料填充质量和加工介质[12]。使用70目、80目、90目、100目、150目和160目筛网，筛分出平均粒径分别为196、155、101 μm的金刚石磁性磨料。采用L9(34)正交试验，因素水平表如表1所示。

表1 TC4因素水平表Tab.1 TC4 factor level

1.3 试验结果

每组试验前用砂纸对 TC4工件进行预处理，在工件上随机选取3个点测量表面粗糙度，取其平均值作为加工前工件表面粗糙度，将工件的表面粗糙度打磨至0.320 μm。采用磁粒研磨光整加工技术，沿工件宽度方向对工件进行2次加工，使用超声清洗器清洗浸没在酒精中的加工后工件2 min，去除工件表面残留油污，随机选取3个点测量表面粗糙度，并取其平均值作为加工后工件表面粗糙度。试验结果如表2所示。

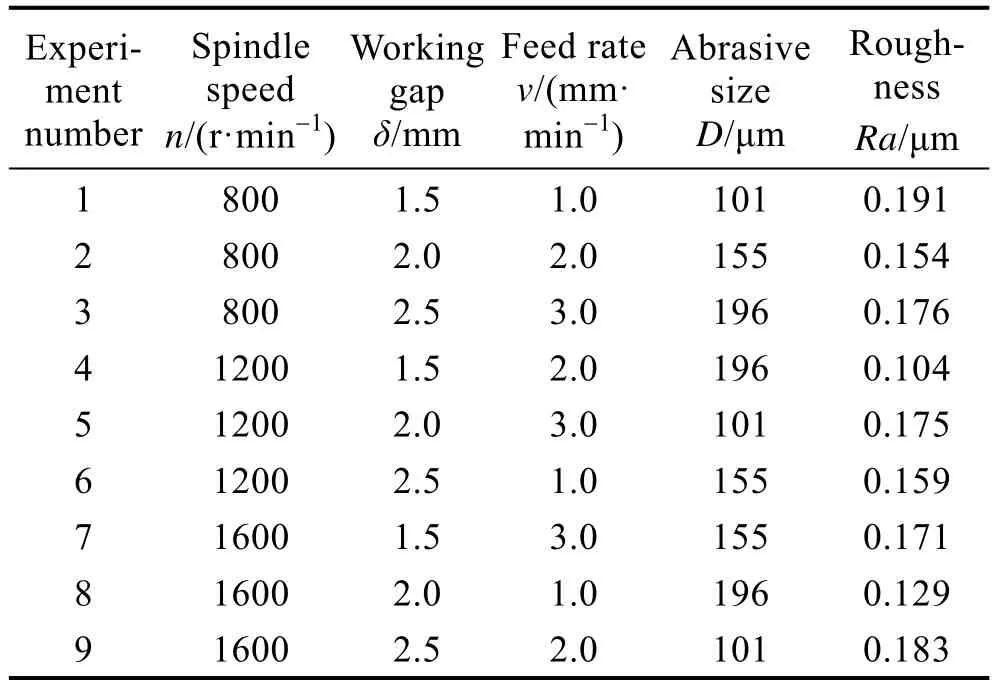
表2 正交试验结果Tab.2 Results of orthogonal test

2 BP神经网络

2.1 BP神经网络的建立

借助Matlab软件建立BP神经网络模型。BP神经网络是人工神经网络杰出的代表，也是当前应用最广的神经网络学习算法之一[13-14]。BP是 Back Propagation的缩写，即BP神经网络是数据正向传播和误差逆向传播。所有输入数据与对应权值乘积的和构成加权和，加权和经过传递函数传递给下一层神经元，得到的预测值与测量值之差，即误差ε。误差ε逆向传播到每一层神经元，调整权值和阈值，循环这一过程直至误差ε满足初始设定的误差标准0.001。神经网络模型是由输入层、隐含层和输出层三部分组成，对于任何一个在闭区间内连续的函数都可以被含有一个单隐含层的BP神经网络模型拟合逼近，所以一个三层的BP神经网络就可以满足输入变量与输出变量之间的映射关系[15]。输入层由主轴转速n、加工间隙δ、进给速率v和磨料粒径D四个神经元构成，隐含层的神经元个数根据经验公式(1)确定，输出层由表面粗糙度Ra一个神经元构成。

式中：h为隐含层神经元个数；n为输出层神经元个数；m为输入层神经元个数；a为调节系数，a∈[0,10]。

训练函数设置为 trainlm。传递函数为 S型正切函数tansig，因为函数tansig在区间[-1,1]之外的区域变化平缓，所以将输入数据归一化到区间[-1,1]内，以避免输出数据区分度小。同时归一化还可以避免数据之间的范围过大，而导致网络模型收敛速度慢和小数据被大数据湮没的问题。使用公式(2)对数据进行归一化：

式中：y为输出数据；x为输入数据；xmin为输入数据最小值；xmax为输入数据最大值。

根据式(1)得出隐含层的神经元个数范围为[3,13]，经试验，神经元个数与模型训练误差的结果如表3所示。当隐含层的神经元个数为12个时，模型训练误差较小，因此选择隐含层的神经元个数为12。构建的BP神经网络模型如图2所示。

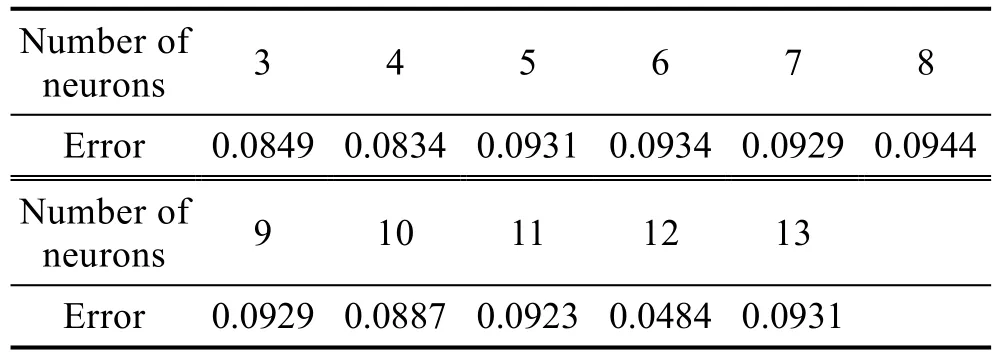
表3 模型训练误差Tab.3 Model training error

2.2 BP神经网络模型的检验

用正交试验得到的 9组数据对建立好的模型进行训练和检验。随机对9组试验数据进行编号，通常选用数据总体的80%作为训练样本，因此随机抽取其中7组数据作为训练样本，剩下的2组数据作为测试样本。建立好的BP神经网络模型通过学习训练样本中的数据，建立输入数据和输出数据之间的关系，用测试样本中的数据来检验模型拟合的好坏。BP神经网络自身并不能判断数据拟合的好坏和预测的准确程度，于是引入决定系数R2来判断建立的网络模型是否达到所需要求[16]。

R2一般用于评估预测值和真实值的吻合程度，是预测值的样本方差和真实值的样本方差的比值，在数学上可以表示为被解释平方和与总离差平方和的比值，如公式(3)—(5)所示。

式中：Y为测量值；为预测值；为平均值；ESS为被解释平方和；TSS为总离差平方和。

总离差平方和等于被解释平方和与残差平方和之和，如公式(6)所示，进而R2可以表示为公式(7)的形式。

式中：RSS为残差平方和。

观察公式(7)可以发现，R2越接近于1，说明预测值与真实值越接近，预测值与真实值的拟合度越高，模型预测越精准。预测结果R2=0.9976，预测值与真实值的拟合度高，如图3所示。预测值与真实值的误差如表4所示，可知预测值与真实值的两组误差分别为1.15%和1.39%，在可接受范围之内，保存训练好的BP神经网络模型，便于遗传算法调用。

表4 测试样本预测值与真实值对比Tab.4 Comparison of predicted data with real data of test sample

3 基于遗传算法寻优

3.1 参数设置及寻优结果

遗传算法是以达尔文进化论中自然选择和遗传机理为基础建立的数学计算模型，舍弃固有的搜索方式，模仿自然界生物的遗传进化过程[17-18]。把目标条件表面粗糙度Ra作为适应度，将待优化参数主轴转速n、加工间隙δ、进给速率v和磨料粒径D中的个体转化为一个个独立的染色体，对这些独立的染色体编码，进行染色体之间的选择、遗传和变异过程。调用训练好的BP神经网络模型，设定迭代次数为200次，种群大小为20个，交叉概率为0.4，变异概率为0.2。以适应度作为评价标准，根据优胜劣汰的法则，不断得到更加优化的群体，在最优群体的范围内搜索最优个体，实现遗传算法寻优功能。输入变量的寻优范围如表5所示。

经过200次迭代后，搜索到最优的表面粗糙度是0.0951 μm，适应度曲线如图4所示，此时的工艺参数值为：主轴转速1021.26 r/min，加工间隙1.52 mm，进给速率1.04 mm/min，磨料粒径197.91 μm。

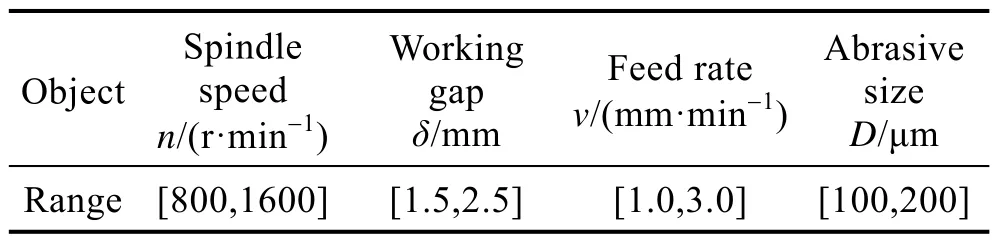
表5 输入变量寻优范围Tab.5 Optimization scope of input variables

3.2 寻优结果检验

使用寻优得到的数据进行试验，其他试验条件保持不变，考虑到试验材料及设备的客观条件，在满足试验设备所能达到条件的前提下，尽可能小地改变计算得到的数据。对试验参数进行调整，调整后的试验参数及试验结果对比如表6所示。

经过3组结果检验试验，试验得到的数据与预测得到的数据误差均小于2.21%，在可接受范围内。经分析，误差产生的原因有：（1）试验结果测量时，测量和读数存在误差；（2）BP神经网络模型建立时，训练样本数量少导致的误差；（3）根据实际加工条件调整得到的最优工艺参数与计算得到的最优工艺参数之间的差值所产生的误差。

TC4材料加工前后的表面粗糙度、表面纹理和加工效果对比如图5—7所示。结果表明，经磁粒研磨光整加工后，TC4材料表面粗糙度下降明显，工件表面的划痕和毛刺被大量去除，加工表面从模糊不清到镜面效果，工件的表面质量提高，有利于提高TC4工件的使用寿命。

表6 寻优结果试验Tab.6 Test of optimization result

4 结论

1）根据正交试验结果，建立了输入量为主轴转速n、加工间隙δ、进给速率v和磨料粒径D，输出量为表面粗糙度Ra的BP神经网络模型，使用决定系数R2对模型预测结果进行评判。所建模型的预测误差小于 1.5%，实现了所建模型在训练样本较少的情况下的准确预测。

2）基于遗传算法对磁粒研磨TC4材料工艺参数优化，计算得到当主轴转速为1021.26 r/min、加工间隙为1.52 mm、进给速率为1.04 mm/min、磨料粒径为197.91 μm时，表面粗糙度最小，为0.0951 μm。

3）采用调整后的优化工艺参数进行 3组验证试验，得到的表面粗糙度分别为 0.093、0.093、0.094 μm，与计算得到的最优表面粗糙度误差均小于2.21%，有效降低了TC4材料的表面粗糙度，提高了TC4材料的表面质量。