基于扩展卡尔曼滤波器的锂电池SOC估算仿真研究*
2020-03-04李立伟
王 越 李立伟
(青岛大学自动化与电气工程学院 青岛 266071)
1 引言
为延长锂电池寿命、改善锂电池的使用性能,动力电池组在使用中需要配备一套电池管理系统(BMS,Battery Management System),BMS需要具备均衡功能以及电池组状态监测的功能[1]。SOC估算是电池组状态监测中的重要功能,一般通过百分比的形式直观地反映出当前电池组的剩余电量,合格的SOC估算能为使用人员或智能设备提供一个准确的剩余电量参考,防止过充、过放对电池组带来的损害[2]。
现有的BMS大多采用安时积分法配合开路电压法的方式对SOC进行估算,不仅在使用上受到限制,估算的精确度也难以得到保障[3],为改善以上缺点,本文介绍了扩展的卡尔曼滤波器(EKF,Extended Kalman Filter)在SOC中的应用,在Simulink仿真环境下建立了电池模型、搭建锂电池充放电模拟电路、编写EKF程序对SOC进行估算,在仿真基础上验证了EKF估算SOC的准确性和可行性。
2 BMS中的SOC估算方法
目前比较常用的SOC估算方法有放电实验法、开路电压法、安时积分法、神经网络法、卡尔曼滤波法等,使用放电实验法时需要使电池组停止工作,不适合应用在动力电池组中;而神经网络法需要大量的参考数据进行训练,时间成本使得其在BMS中的应用并不广泛[4~6]。故本文暂针对BMS中常用的开路电压法、安时积分法以及卡尔曼滤波法进行讨论。
2.1 锂电池等效模型的建立
锂离子电池内阻包括符合欧姆定律的欧姆内阻和呈容性的极化内阻,一阶戴维宁等效模型能较准确地模拟电池的充放电动态特性,在Simulink环境下建立锂电池一阶戴维宁等效模型,如图1所示。E为锂电池电动势,在数值上近似于开路电压;R1为欧姆内阻,引起电池充放电瞬间端电压的突变;R2、C1分别为极化电阻和极化电容,引起电池充放电时端电压的渐变[7~8]。
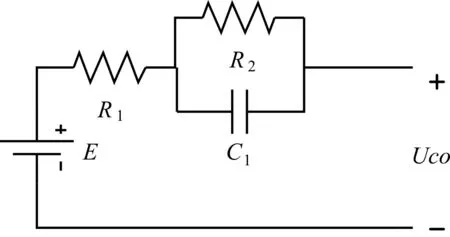
图1 一阶戴维宁等效模型
2.2 开路电压法
由于锂电池的开路电压(Open Circuit Voltage,OCV)在数值上与电动势近似,而SOC值与电动势之间存在对应关系,故可通过读取电池的开路电压来估算SOC。在仿真环境下对容量为10Ah、标称电压为3.7V的锂电池进行电流为1C的放电,每放电5%后静置1800s以使开路电压完全稳定,直至SOC值为0%。测得SOC与OCV的对应关系如图2所示,可以看出在SOC值两端SOC与OCV对应关系较为明显,而在中间部分OCV的变化幅值并不明显。在中间部分容易引起SOC估算误差,以及需要长时间静置使得开路电压稳定的特点使得开路电压法并不是一种理想的SOC估算方法。

图2 SOC-OCV曲线图
2.3 安时积分法
由于电池内部参数是不断变化且难以测量的,安时积分法直接将整个电池看做一个节点,通过不断测量电池输入、输出电流并积分对SOC进行估算,其估算公式为
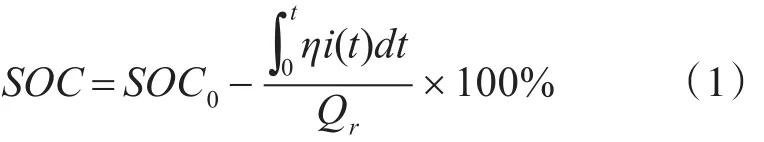
其中,SOC0表示初始SOC值,Qr为额定容量,η为充放电倍率为时间t内流过的电量。可见安时积分法的精确度完全依赖于初始SOC值的精确度,且随着时间的增加,电流的测量误差将会积累,因此安时积分法常结合其他方法使用[9]。
2.4 卡尔曼滤波法
卡尔曼滤波器用来估计一个由线性随机差分方程所描述的时间离散系统的状态量,从观测值中得到系统状态量在最小均误差意义下的最佳逼近值。它利用前一时刻估计值和现时刻的观测值来更新对状态变量的估计,其对初始值的不敏感性非常适合应用在SOC估算中[10~11]。其离散模型为
状态方程:
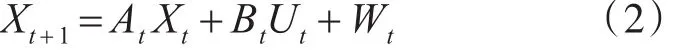
观测方程:

其中A、B、C、D分别为状态转移矩阵、状态量控制矩阵、观测矩阵与观测量控制矩阵,均由系统特性所决定;X、Y、U分别为状态量、观测量、控制量;Wt、Vt分别为过程噪声和观测噪声,一般为方差为0的高斯白噪声。在BMS中通常可以测量电池的电流及端电压,在不考虑充放电倍率的情况下,结合安时积分法与一阶戴维宁等效电路,得出SOC估算中离散的状态方程与观测方程为

其中I为流过电池的电流,UC为极化电容两端的电压。除了SOC之外,将UC作为另一个状态量,根据一阶电路全响应方程计算UC

将UC作为状态量加入状态方程,得到SOC估算中的卡尔曼滤波器计算公式:

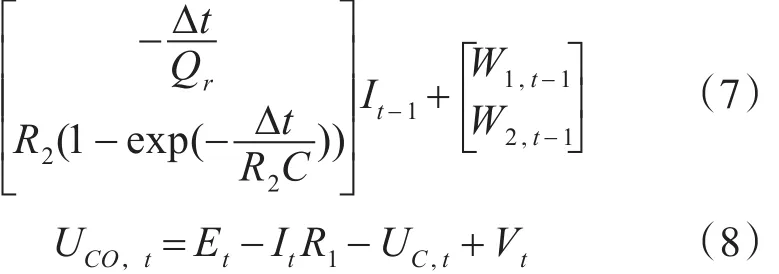
其中Et为电池的电动势,与状态变量SOC之间存在对应关系

通过图2显然这个对应关系是非线性的,而普通卡尔曼滤波器只适用于线性系统,故因此提出了扩展的卡尔曼滤波器。
3 扩展卡尔曼滤波器估算SOC
扩展的卡尔曼滤波即通过线性变换将非线性系统转换成线性系统,使之适应卡尔曼滤波[12]。对于非线性系统,其离散的状态空间模型如下:


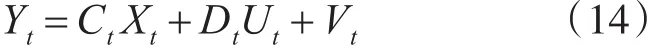
至此任一时刻的状态转移函数和观测函数全为线性系统,那么结合以上公式,SOC中扩展卡尔曼滤波器的离散模型为
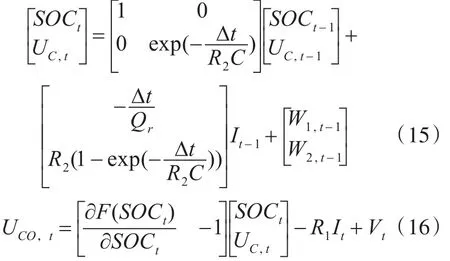
扩展的卡尔曼计算公式及流程如下:

3.1 参数辨识
得出扩展卡尔曼计算公式之后,还需要对公式中的各参数进行辨识,即锂电池等效模型中的R1、R2、C1。对锂电池进行以1C电流放电5%、静置180s的循环放电,读取锂电池的开路电压,截取4000s~5000s绘制放电电流、电压图。如图3所示,在电流由10A降为0A的瞬间,因欧姆内阻的存在使得电池电压瞬间升高,通过Workspace中的数据得出ΔU1为0.037V,故欧姆内阻R1为3.7mΩ。
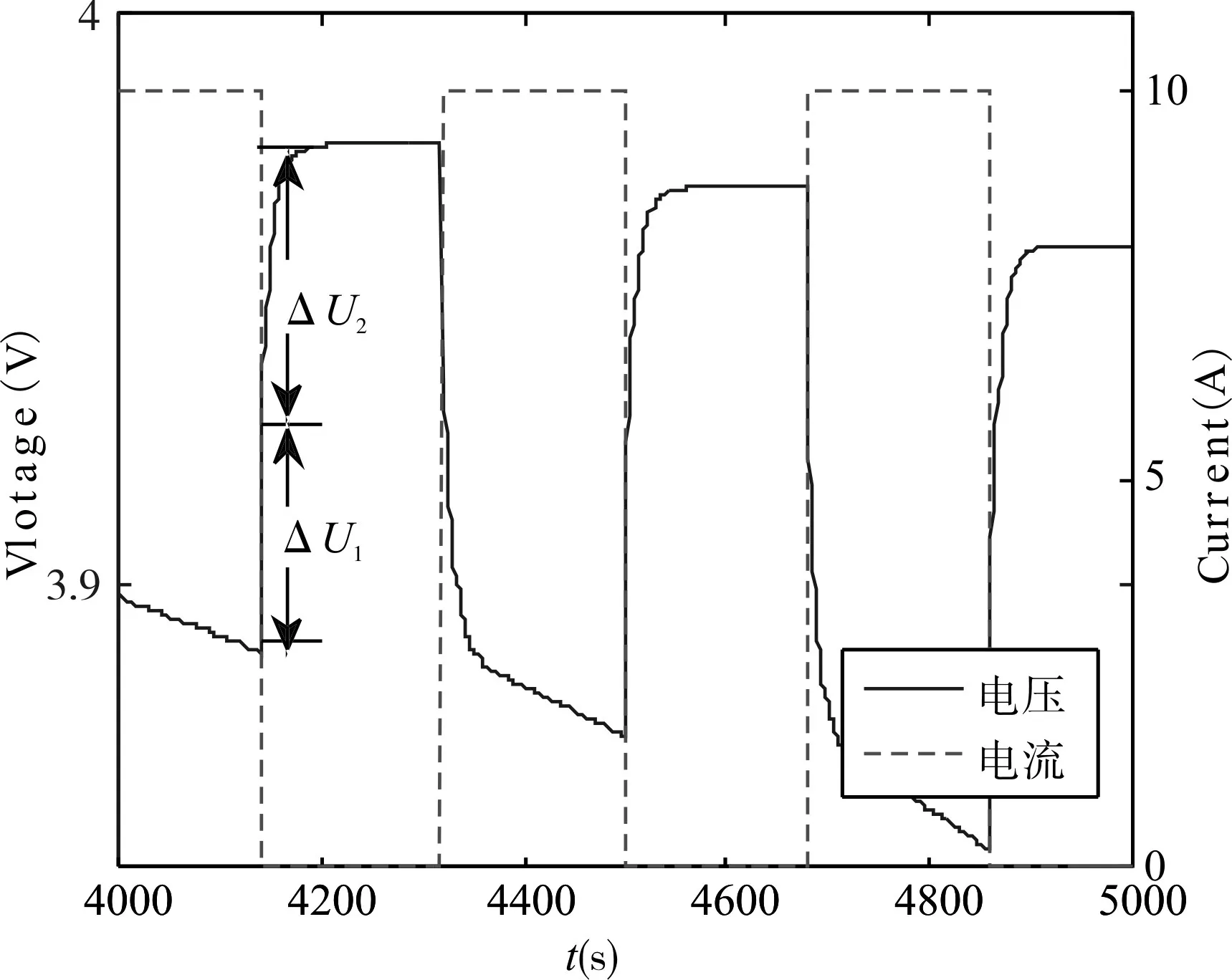
图3 锂电池放电曲线图
由于在锂电池中极化内阻会随SOC的变化而改变,故 R2、C1是SOC的函数,以t为4140时刻为例说明极化电阻与极化电容的辨识过程。当t=4140s时端电压由3.8879V瞬间升至3.9249V,静置至电压稳定后测得电压为3.9771V,故ΔU2等于52.2mV,得出R2=5.22mΩ。根据一阶电路的零输入响应公式:
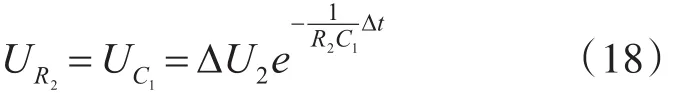
在电压缓慢上升的过程中任取时间t=4170s,由数据得此时端电压为3.9745V,那么此时电容上的电压 UC1为 0.0026V(即 3.9771~3.9249),又有Δt=30s,将各数据代入式(18)计算得出此时C1为1915F。为得出R2、C1随SOC的变化关系,分别对SOC为10%至90%共17个点进行参数辨识,并通过cftool工具进行拟合,拟合曲线如图4所示,图中横坐标SOC的1即为100%,拟合公式为
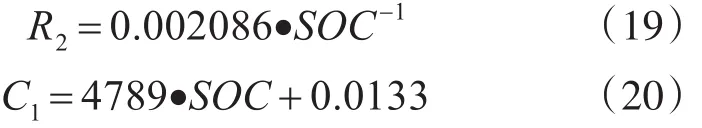
3.2 SOC-OCV曲线拟合
同样地对锂电池进行以1C电流放电5%、静置180s的循环放电,待电压稳定后读取开路电压。因电池的过充、过放对电池损耗较大,故暂不研究极端情况,取SOC为20%至90%区间进行拟合,拟合曲线如图5所示,公式为


图5 SOC-OCV拟合曲线
4 扩展卡尔曼滤波器估算SOC仿真实验
为验证扩展卡尔曼滤波器估算SOC的可行性,在Simulink环境下搭建锂电池充放电电路。如图6所示,CCS为压控电流源,通过信号发生器产生一定幅值、一定周期的电平驱动CCS以实现对锂电池的均衡充放电;由于扩展卡尔曼算法较为复杂,不适合使用Simulink自带模块搭建,故将算法写入S-Function模块,电池端电压作为观测量、电池电流作为控制量输入S-Function,经S-Function计算处理后输出SOC估算值;同时为了调试观察,利用Scope模块观测各量状态,并通过Simout模块将观测数据输出到Workspace中用于分析。

图6 Simulink仿真电路
对锂电池进行电流为1C的循环放电,每放电180s后静置120s,并且通过S-Function对输入电压、电流分别加入方差为零、幅值分别为0.005、0.01的高斯白噪声。将锂电池模型的初始电量设置为80%,即认为电池初始的真实电量为80%,为验证扩展的卡尔曼滤波法对SOC初始值的不敏感性以及对SOC误差的矫正能力,分别设置输入滤波器的初始SOC为100%和30%,通过仿真实验与安时积分法进行对比,仿真结果如图7、8所示,分别作两种情况下的EKF估算值与理论值的残差图如图9、10所示。
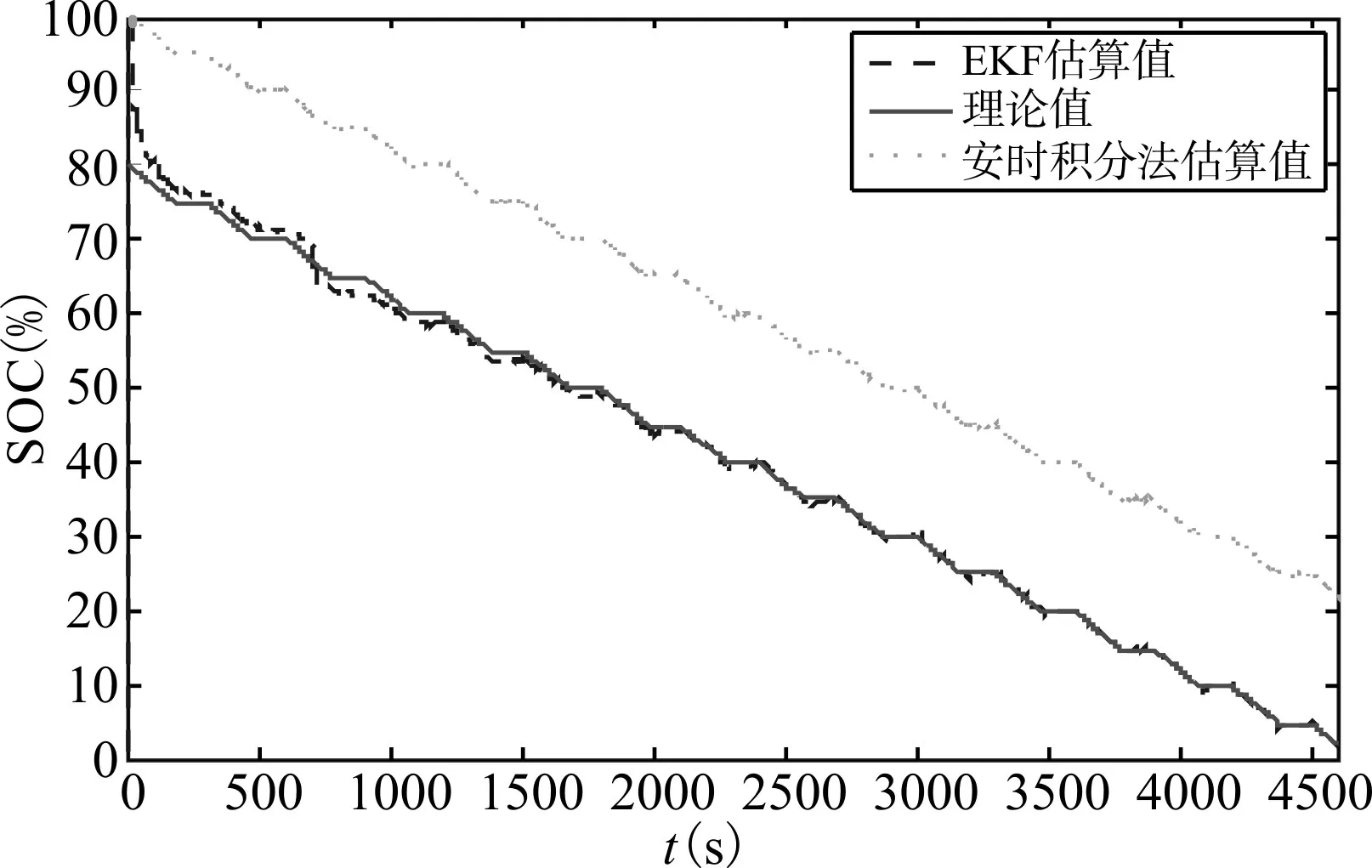
图7 初始SOC为100%时的EKF估算SOC曲线图

图8 初始SOC为30%时的EKF估算SOC曲线图
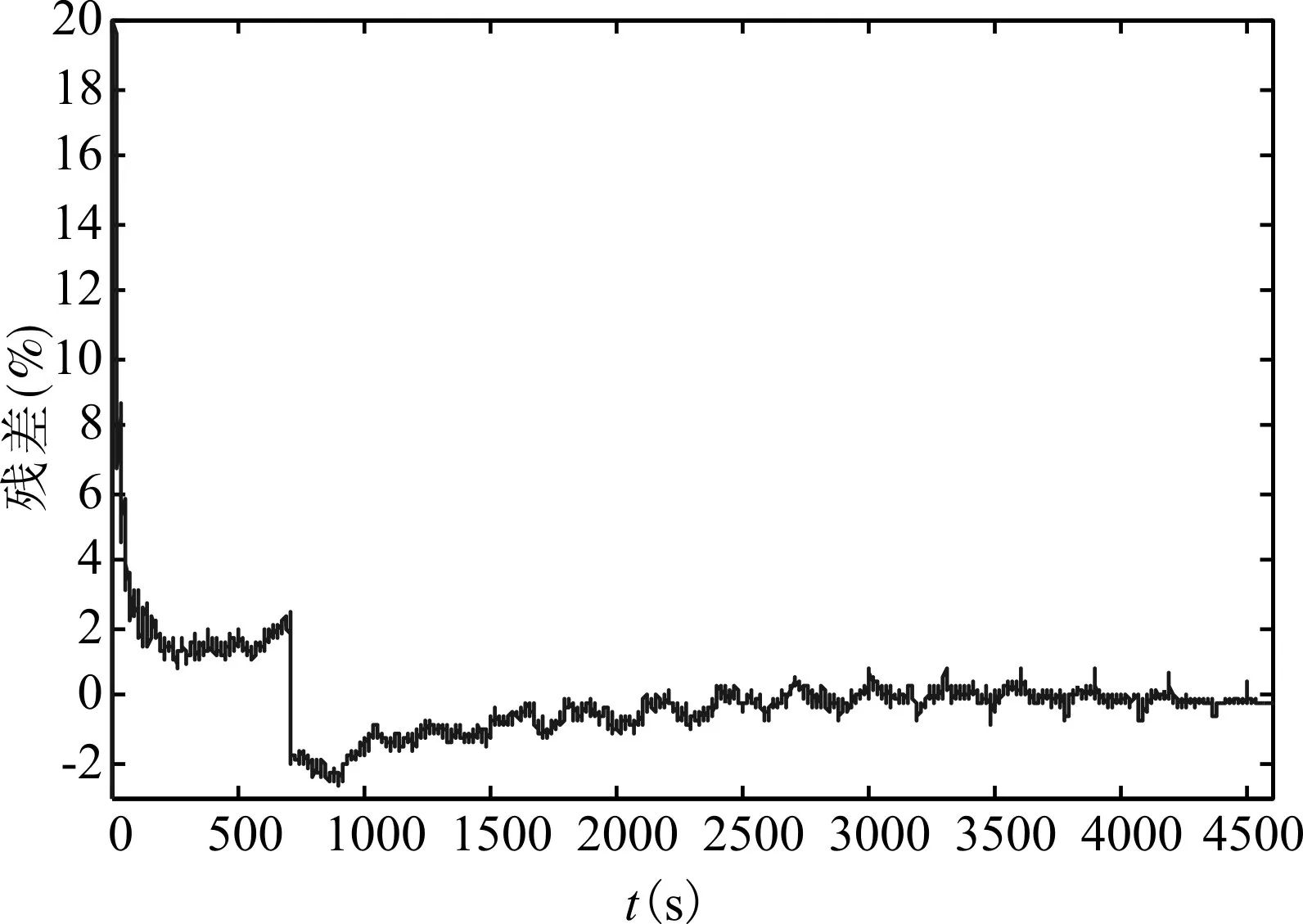
图9 初始SOC为100%时的EKF估算SOC残差图

图10 初始SOC为30%时的EKF估算SOC残差图
通过仿真结果得出以下结论:单纯使用安时积分法时,若初始值有误,则初始误差将会一直存在,大大降低了SOC估算的准确性;使用EKF估算SOC对初始值不敏感,EKF能在短时间能矫正SOC值,通过对数据分析可以得出,在初始SOC与真实SOC相差50%时,EKF能在60s内将误差矫正至5%以内;在EKF完成大误差矫正后,其估算误差因加入高斯白噪声的缘故在-2%至2%之间浮动,最大不超过3%;且随着时间的推进、迭代次数的增加,EKF误差将越来越小,估算SOC值越来越逼近真实值。
以上结论证明了EKF在SOC估算中的可行性、准确性与对初值的不敏感性。
5 结语
通过实验证明了扩展卡尔曼滤波器在SOC估算中的良好应用,其具有较高的可靠性与稳定性。工程应用中可将算法移植到各种嵌入式设备中,如电动汽车BMS主控、航天锂电池供电设备、精密供电仪器等用锂电池供电的场合,具有一定的实用价值[15]。本文实验建立在仿真基础上,实际应用中仍需考虑许多其他影响因素,如温度、放电倍率、电池老化程度等对SOC估算的影响,但对于扩展的卡尔曼滤波器而言,只要模型建立可靠、参数辨识准确,就可以将SOC估算值向真实值上靠拢。下一步将结合实验室条件对锂电池进行实际参数辨识,并将其他影响因素加入到算法中,以期更准确地对SOC进行测量。
