基于经验小波变换的结构损伤特征提取*
2020-03-04王彩霞刘义艳
王彩霞 刘义艳
(长安大学电子与控制工程学院 西安 710054)
1 引言
结构的损伤会引起结构的刚度、阻尼和固有频率的变化,结构的动力响应也会随之改变,由于振动响应信号中包含有丰富的损伤信息,所以恰当的信号分析方法有利于提取结构损伤特征,为结构损伤诊断和健康趋势预测提供基础[1]。1998年Norden E Huang等提出了经验模式分解(EMD)[2],该方法是将多分量的非平稳信号自适应分解为多个本征模态函数(IMF)分量,再对各个分量进行Hilbert变换得到瞬时频率及瞬时幅值,但是它仍存在一些主要问题,如模态混叠、端点效应和缺乏完备的理论基础等问题[3~5]。一些学者提出消除端点效应的方法来改善 EMD性能[6~8],应用聚类经验模态分解(EEMD)方法克服模态混叠现象[9],但是在噪声环境下EEMD提取有用信号分量时,计算量和计算时间增加,效果也不是很好。因此,法国Gilles结合自适应经验模态分解的优势和小波分析理论提出经验小波变换[10],对非平稳信号的处理得到很好地应用,主要是将获取的原始信号进行频谱的自适应划分,构造适当的小波滤波器组,提取支持Fourier谱的调幅-调频(AM-FM)成份。国内外已有研究学者将EWT作为一种新的信号处理分析工具应用于一些非平稳信号研究,并取得良好的成果[11~18]。本文将EWT方法应用于结构的损伤特征提取中,并与EMD方法进行比较,仿真结果验证了EWT的有效性,最后将该方法结合Hilbert变换应用到实际工程结构损伤的提取中,实验结果进一步验证了经验小波变换的有效性。
2 经验小波变换(EWT)
2.1 经验小波变换
经验小波变换,首先将原始信号分解成N+1个模态函数之和:

为提取不同频段的AM-FM成分,将傅里叶支持的区间[0,π]划分为N个连续部分,就是N+1个边界,除了0和π,剩余的N-1个边界通过检测频谱中的局部最大值进行从大到小排序,设极大值个数为M,若M≥N,则保留前N-1个极大值,若M<N,保留所有的极大值并设置N为合适的值。
Gilles根据 Littlewood-Paley和 Meyer[19]小波的建立思维创造出经验尺度函数与经验小波函数。然后由小波变换方式来表达经验小波变换(EWT)。假设Fourier变换和其逆变换及复共轭分别由 f^(·)、FF(·)和 fˉ(·)表示。细节相关系数和近似相关系数的表达式如式(2)和(3)所示。

式中,φn、φn分别是经验小波函数和经验尺度函数。
2.2 Hilbert谱分析
通过EWT的分解,得到待分解信号的各个AM-FM分量后,再对各个调幅-调频函数 fk(t)进行希尔伯特变换[20],提取具有表征特性的瞬时幅值和瞬时频率,同时构造出Hilbert谱。函数f的希尔伯特变换的定义如下:

构造解析信号得:

从以上公式可以得到振动信号幅值的时频分布:

3 仿真实验与分析
采用两个仿真信号x1(t)和 x2(t)进行分析,x1(t)由三段单调信号、调频信号和不同时间段的信号 x11(t)、x12(t)和 x13(t)组成,其中 t∈[0,1],采样频率为 fs=2000,采样点数为2000,信号表达式如式(7)所示。

仿真信号x2(t)由余弦信号、调频信号、调幅信号和均值为0的白噪声 x21(t)、x22(t)、x23(t)和n(t)信号叠加而成,此信号可模拟频率、能量各异的信号的分量,可以很好地验证EWT的分解能力和抗噪性能,信号表达式如式(8)所示。
两个仿真信号的时域波形图如图1所示。

为了验证该算法的有效性,图2是两种分解方法的对比图。由图2可知EWT能够精确地提取两个信号的特征分量。而EMD对x1(t)分解分量很少或有部分缺失,模态分量存在混叠现象,对x2(t)分解出8个模态函数分量和一个余项,过多的分解层数,使迭代次数增加,效率大大下降,其中模态分量c6是原始信号中的4Hz余弦分量,而调频信号分量与调幅信号分量被完全混杂在噪声信号中。

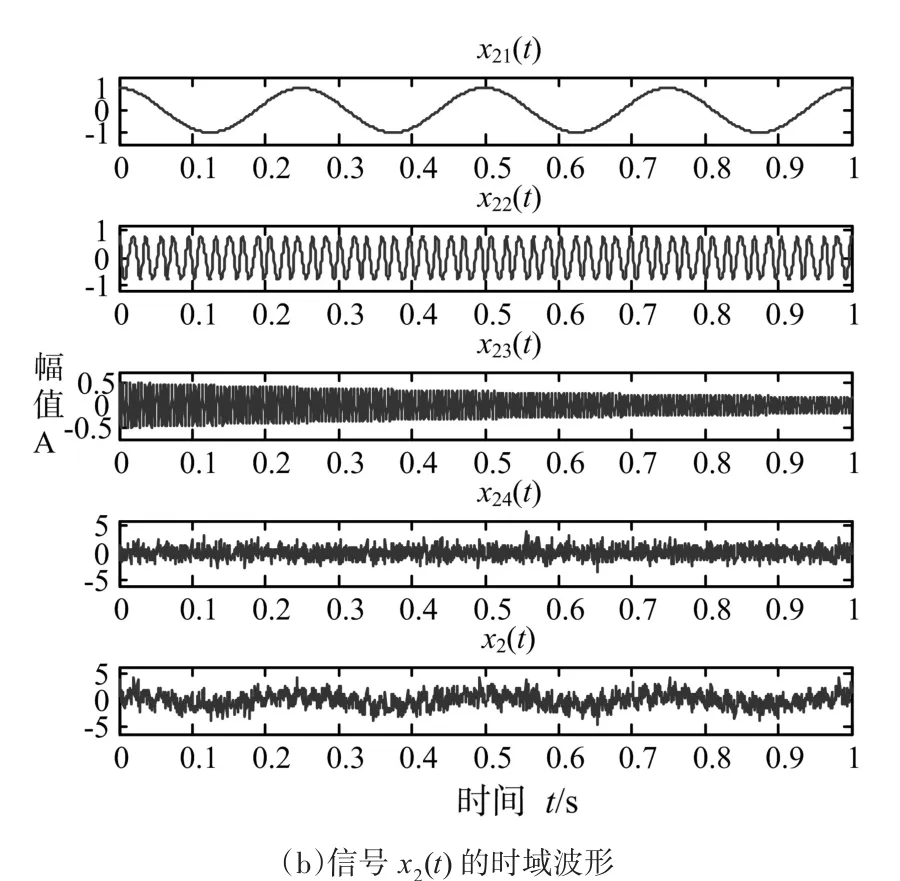
图1 信号的时域波形图

图2 信号的EWT和EMD分解
4 实际工程振动信号的实验与分析
4.1 实际工程振动信号的EWT分解
本节实验数据来自ASCE实际工程振动加速度信号的采集(第二期)[21],是UBC地震工程实验室实际测量得到的。损伤体现为取掉结构板层间的斜支柱或松动螺栓的形式。工程振动数据选取电动机振动激励下产生的加速度信号,采样频率是200Hz,择取6000个数据进行分析研究,选取以下四种工况进行研究,如图3所示。
1)无损伤状况;
2)东南侧1层与4层一个跨的斜支柱取掉;
3)东侧全部层的斜支柱与2层朝北的斜支柱取掉;
4)全部层的斜支柱取掉,加之全部层东北侧4层横梁端头的螺栓松动状况。

图3 损伤模式
图4 ~5为四种不同工况下采集的加速度振动信号及四种工况利用EWT方法分解得到的信号。

图4 四种工况采集的加速度信号图

图5 四种工况下加速度信号的EWT分解图
4.2 振动信号频谱边界探测和Hilbert变换
为了更好地区分有无损伤信号,图6是对应图4~5中四种工况下的信号频谱图。其中图(a)、(b)、(c)、(d)是四种工况的N分别为2,7,11,6所对应的信号频谱边界探测,其中图(a)没有探测到频谱的边界,图(b)、(c)、(d)探测到损伤信号大概分布在20Hz、30Hz左右的低频区。结构发生损伤时,其本征频率随之发生变化,而且在不同的损伤工况下,结构的信号频谱也有很大的不同。四种工况的EWT分解得出了多个分量,经实验后发现,结构损伤特征向量包含在第一个AM-FM分量中,分别对四种工况包含有损伤信息的分量进行Hilbert变换,结果如图7所示。
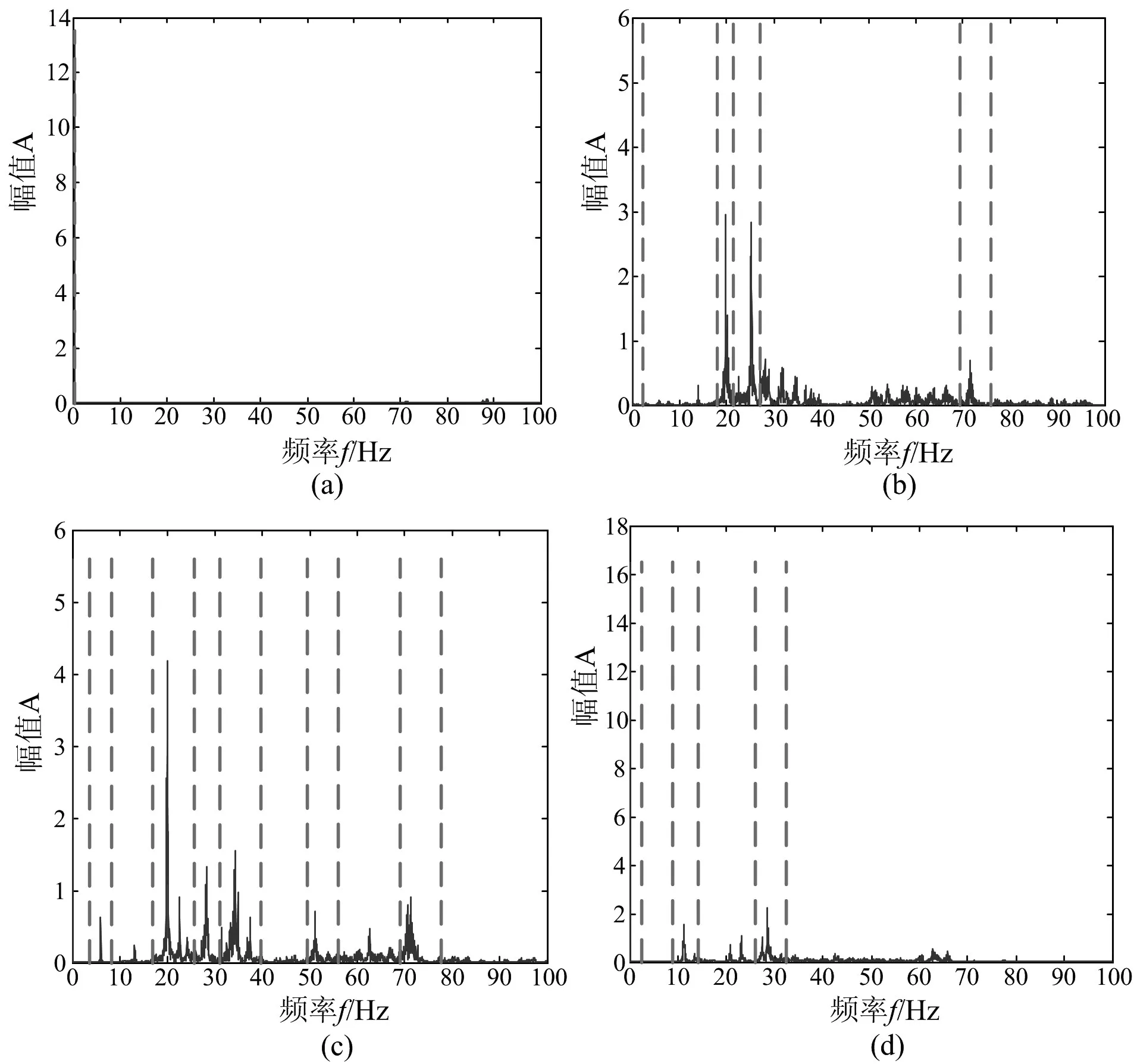
图6 四种工况的信号频谱图

图7 四种工况的Hilbert变换
由图7可知,在四种工况下,损伤工况不同对应的瞬时频率也不同,无损伤的瞬时频率波动幅度小于有损伤的。结果表明,结构受到损伤越严重,瞬时频率下降的越低。实验结果计算得到四种工况的瞬时频率均值约为40.6584Hz、28.3353Hz、27.7718Hz和23.7131Hz。理论值[22]下四种工况的固有频率值分别是40.983Hz、28.446Hz、27.539Hz和23.427Hz,该结果与本文识别的结果是大致相同。
5 结语
本文提出了一种基于经验小波变换和Hilbert变换相结合的结构损伤特征提取方法,并应用于仿真信号与实际工程振动信号。结果表明:与EMD方法相比,EWT分解的模态少,能很好地消除模态混叠及分量缺失的现象。EWT相比EMD的理论依据更加健全,运行时间优于EMD方法,且EWT方法结合Hilbert变换应用到实际的工程振动数据中,能够有效地提取结构损伤的特征频率,为进一步的结构损伤预测奠定了基础。
