基于新型切换Lorenz混沌系统的图像加密算法研究*
2020-03-04付正李嵘
付正 李嵘
(河南工业技师学院 郑州 450007)
1 引言
互联网技术快速发展使得多媒体文件在越来越多的地方得到了应用,多媒体文件的传输安全也愈加重要。安全传输图片等信息已经成为当下研究的热门问题。1989年,美国学者R.Matthews首次采用 Logistic映射生成大量的伪随机数据[1~2]。随着对伪随机数据的不断研究,学者们发现混沌系统非常适合图像的加密。因此,Logistic混沌系统、切换Lorenz混沌系统逐渐被应用到图像加密中[3~5]。2004年,G.R.Chen,Y.Mao,C.K.Chui等对混沌图像加密技术进行了研究,并针对图像加密效果进行了评价,提出了 NPCR 和 UACI评价指标[6~7]。2012年,Y.ZHANG等提出了基于明文关联的混沌图像加密方法[8]。这些混沌加密方法在图像加密中得到广泛应用,取得了较好的加密效果。
切换Lorenz混沌系统是一种典型的混沌系统之一,专家学者们对该混沌系统研究较多,提出了多种不同的新型Lorenz系统,如典型的Chen系统、Lü系统等[9~11],这些系统已被应用到图像加密中。研究发现,单一的混沌系统加密算法存在密钥空间小,加密安全性不足。为了解决该问题,论文提出新型切换Lorenz混沌系统,采用多种混沌系统图像加密的思路,将Arnold映射和二维Logistic混沌映射结合到一起,构成新型图像加密系统。该加密系统具有结构复杂,密匙空间大等优点,加密安全性高[11]。
2 新型切换Lorenz混沌系统
论文采用的新型切换Lorenz混沌系统的数学模型为[12~14]:

式(1)、(2)中,a,b,c为系统常量。其中a=20,b=14,c=10.6;h为Lorenz混沌系统控制参数。
论文参考文献中对式(1)的动力特性进行了分析,系统控制参数h与Lyapunov指数的关系如表1所示[6,8]。

表1 系统控制参数h与Lyapunov指数的关系
根据参考文献中系统控制参数h与Lyapunov指数的关系的讨论分析,论文选用h=2.8,此时,混沌系统的Lyapunov指数较高。
3 图像加密系统
混沌图像加密系统对图像加密的流程基本是首先对图像进行离散和多次置乱,然后进行扩散处理从而得到密文图像。论文采用的图像加密系统具体流程见图1。根据新型切换Lorenz混沌系统数学模型式子(1)和四阶龙格-库塔方程对待加密的明文图像进行离散,同时采用Arnold映射对明文图像进行第一次置乱,置乱后进行“异或”的扩散处理。在第一次置乱的基础上,为加强文件的安全性,采用二维Logistic映射对图像进行二次置乱,并进行“循环移位”的扩散处理[14~15]。经过两次置乱后,最终得到加密后的密文图像。加密与解密过程相反,不再赘述。

图1 图像加密流程
3.1 第1次置乱
混沌图像加密系统需要对明文图像各个像素点的位置进行置乱操作,已达到加密的效果。在置乱过程中,虽改变了像素点的位置,但是不改变像素的值。
本文引入四阶龙格-库塔方程[14](式(3)所示),对式(1)进行离散,离散后得到伪随机浮点数序列s。

利用得到的伪随机浮点数序列s对明文图像P进行置乱。首先将s进行坐标变换得到一维序列X,将明文图像P的任一点坐标(i,j)进行Arnold变换[14],同时与一维序列X进行模运算,得到新坐标(p,q)。变换过程如下:
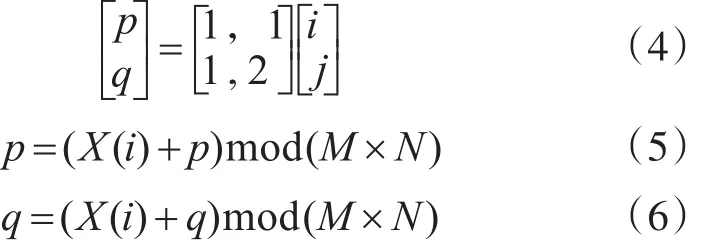
将明文图像原始像素点坐标用新坐标替换,从而完成图像第一次置乱。
3.2 第1次扩散
经过像素点位置置乱后,需要对像素点的值进行更改——扩散。如此才能保证图像加密更加安全。第1次扩散从正向和逆向两种方式展开。将上节中已经得到的置乱图像B转换为一维矩阵K,按照正向和逆向两种运算方式(式(7)~(10)),将明文图像像素点隐藏到密文像素点中,最终得到加密图像 C[14]。
正向(按i从1到M×N)运算:

逆向(按i从M×N到1)运算:
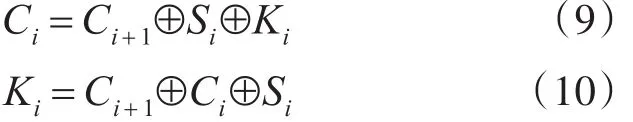
3.3 第2次置乱
在第1次置乱和扩散的基础上,为了进一步增加图像加密安全性,本文采用二次加密。第2次置乱采用二维Logistic映射对第1次置乱扩散后的图像C进行再次置乱,将置乱后的矩阵记为D。论文采用的二维Logistic映射[14]为

3.4 第2次扩散
经过第2次置乱后,论文对第2次置乱后得到的矩阵D进行循环左移位的运算,计算方法如式(12)和式(13)所示。
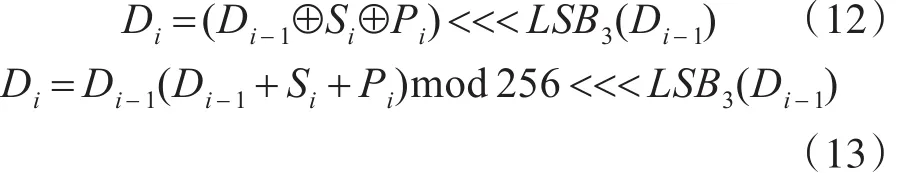
式(12)和式(13)中,LSB3指最少3位。
经过循环左移位运算后,最终形成了二次加密的图像D。
4 图像加密系统性能测试
按照上节图像加密的方法,论文选用了研究常用的典型灰度图像Lena图像作为论文加密测试对象。作者选用了一台HP电脑(配置为:CPU:Intel Core I5,内存8G,安装有Matlab 2014a软件)作为测试工具。测试选用密匙 Key={x0,y0,z0,n} ,其中x0,y0,z0为式(1)的初始值,n为迭代次数。论文采用Matlab实现了上节新型切换Lorenz混沌系统图像加密算法,将Lena图像代入以后,实现的加密效果如图2所示。

图2 Lena图像加密效果
4.1 密钥空间分析
图像加密系统需要具有较大的密匙空间,如此才能防止各类网络攻击,保证文件的安全。一般来讲,当密钥空间大于2100时,文件加密安全性较高。论文的Lorenz混沌图像加密系统,经过两次加密,密匙空间较大。文中加密系统的密钥Key={x0,y0,z0,n} ,其中 x0,y0,z0都是 double型浮点数,n为整数,密钥分量 x0,y0,z0的浮点数精度都可达到10-14,密钥空间可达到1014×1014×1014×1014=1056,远远大于2100=1.27×1030。由此看见,论文实现的新型Lorenz混沌图像加密系统具有较大的密匙空间,安全性较高。
4.2 直方图分析
图像直方图能够反映出图像质量特性分布情况,为了更好地分辨出图像情况,论文编写了Matlab程序显示了原始Lena图像和加密后Lena图像的直方图,如图3所示。图中可见,明文Lena图像的直方图波动范围较大,波峰波谷差异明显,能够反映出图像不同像素值的频率分布。而加密后的Lena图像直方图基本均匀显示在矩形范围内,像素点频率分布相仿。这表明经过加密的Lena图像像素点均匀分布,能够起到扰乱效果,加密效果较好。

图3 Lena明文和密文图像的直方图
4.3 信息熵
图像的确定性可以采用信息熵进行评定。一般来讲,图像信息的混乱程度与信息熵成正比,信息熵值高也意味着图像较为混乱。那么对于类似于Lena图像的灰度图,如果灰度值分布较为均匀,则信息熵值较大;反之,亦然。信息熵值计算方法如式(14)所示。

式中:L为图像的灰度等级数;p(i)为灰度值i出现的概率。对于L=256的灰度图像来说,信息熵的理论值H≤8。信息熵越接近于理论值,图像被攻击的可能性越小。
作者对本文加密测试的Lena图像的信息熵值进行了计算,并与参阅的文献中相同图像的其他测试加密结果相对比,结果如表2所示。表中可见,论文的加密方法处理的Lena图像较文献资料具有更高的信息熵值,更接近理论值8。这说明论文加密效果较好,图像混乱程度更高。

表2 信息熵测试结果
5 结语
本文提出了新型的切换Lorenz混沌加密系统,在传统的单次图像加密的基础上,通过采用“置乱-扩散-置乱-扩散”的两次图像加密过程,实现了图像的更高水平加密。论文以Lena图像的加密过程为例,采用Matlab软件编写了相关程序,实现了新型的切换Lorenz混沌加密系统;在此基础上,通过直方图分析、信息熵值分析等验证,表明了论文实现的图像加密算法具有较高密匙空间和信息熵值,混乱效果较好,安全性更高,在未来具有更好的应用前景。
