磁导航AGV纠偏控制模型的研究与设计*

何 翠 杨光永 史雄峰 徐天奇

（1.云南民族大学电气信息工程学院 昆明 650504）（2.通用电气医疗系统（中国）有限公司 无锡 214000）

1 引言

磁导航AGV［1］是工业自动化生产中十分常见的搬运设备，随着工厂自动化程度的不断改型提升，磁导航AGV的应用环境也变得更加复杂多变，为了提升系统运行的稳定性，特别是循迹导航的准确性，许多高校及工业生产领域在AGV纠偏控制方面展开了大量研究。文献［2］基于经典PID控制算法，对PID参数整定研究设计了轨迹跟踪器；文献［3］将PID算法结合智能控制神经网络算法设计了具有自学习功能的自适应PID控制器。文献［4］通过大量的训练和专家理论经验确立模糊规则，提出模糊PID控制算法，但AGV的非完整约束性和非线性导致获取准确参数比较困难，实时性不高，而且当AGV速度过快时可能会引起脱轨，在实际工程应用中不完全可靠。上述文献中的纠偏控制算法均为在PID基础上进行改进的控制算法，其对AGV系统循迹纠偏控制有一定的优化作用，但在实际控制过程中，控制参数需要通过大量实验和理论经验整定得出，且其参数对AGV控制产生的影响比较灵敏，不能达到最优控制。为此文献［5］采用磁导航信号采集点的加权平均进行浮点运算实现AGV纠偏控制，但其运算效率较低，占用过多片上资源，降低了AGV控制的实时响应性。上述算法虽然在各自特定的领域有其优势，但在稳态精度、控制效率、复杂度等方面很难取得最佳性能，往往只能侧重其中某个方面。针对这些不足，本文设计了基于线性二次型［6］（LQR）的纠偏控制模型，推导出LQR控制器最优解，借助AGV运动学模型，进一步推导其控制模型，以提高AGV在不确定环境下的实时性和鲁棒性。

2 AGV运动学模型

本文采用四轮式结构的AGV模型，其中前轮为万向轮，后轮为驱动轮，据其机械结构建立AGV偏移模型如图1所示，OXY是AGV运动的基坐标系，其参数定义如表1所示。

图1 AGV循迹偏差模型

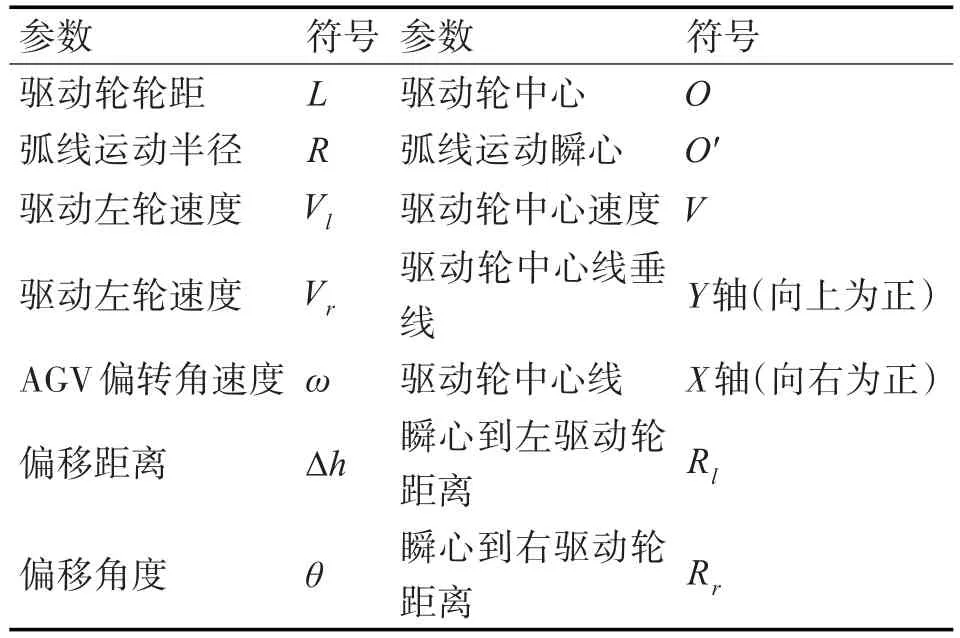
表1 参数定义

上述运动学模型［7～8］基于以下预设条件：

1）AGV在光滑水平面上做刚性运动，无摩擦力；

2）AGV左右驱动轮受力相同，万向轮完全跟随驱动轮运动行驶；

3）磁条铺设平整连续；AGV车体质量、负载等干扰因素对车速的影响忽略不计。

AGV驱动轮通过两个独立的直流电机驱动，控制其转速偏差实现转向、纠偏等循迹任务。假设初始状态，AGV在规定磁条做匀速直线运动，某一时刻受干扰因素影响，脱离磁带发生偏移，做弧线转向运动，其运动学模型推导如下。

AGV瞬时偏转线速度：

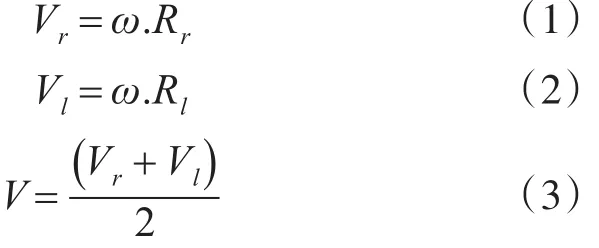
由式（1）～（3）可得AGV瞬时旋转角速度ω和旋转半径R：

V分解为

积分得：

发生偏移dt时间内AGV角度偏差和位置偏差的运动状态方程为

拉氏变换得：

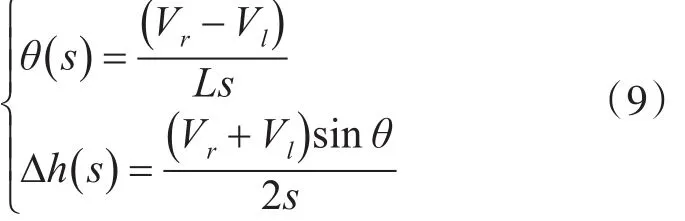
根据直流电机动态过程的微分方程：可推τm.τe.n¨+τm.n˙+n=Kc.Ua+Kf.Tc出左右轮驱动电机与电压之间的关系表示如下：

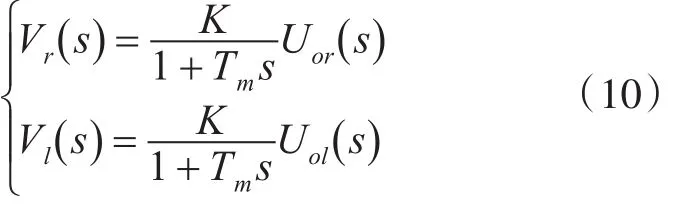
Uor、Uol为驱动轮电枢电压；Tm为响应时间常数。

根据上述推导可建立电动机驱动模型，得出相应的动态结构框图如图2所示。

图2 AGV动态特性结构图

当时间段dt取极小值时对电机驱动模型线性化，将AGV近似看成做直线或圆周运动，此时θ≈sinθ，Uor-Uol=ΔU，得到控制系统的近似线性控制关系如图3所示。

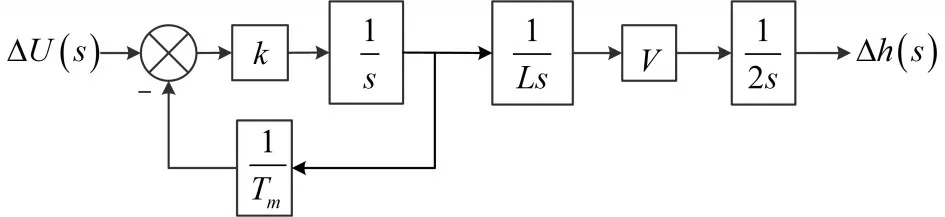
图3 小偏差线性化控制变量图

综上所述AGV控制变量传递函数：

3 控制系统能控能观性分析

由上述推导可知AGV运动状态为

设为AGV运动状态变量，ΔU()s是控制系统反馈输入量，可以得到控制系统状态方程为

：x1=ΔV(s);x2=θ(s);x3=Δh(s)

位置偏差Δh为系统的输出量，则系统输出方程为y˙=Cx+DΔU；其被控系统状态空间数学模型可记为

其中已知参数：Tm=10;L=0.3;V=0.75;则根据系统能控、能观性判断依据［9］：得到该系统即可控又可观，系统数模型建立合理。

4 最优控制器的设计

本文设计的磁导航AGV纠偏控制模型是依据磁导航传感器采集的电信号来确定AGV在行驶过程中的位置和角度偏差，通过上述控制模型计算给出适当的控制量，消除偏差以达到控制目标。其最优控制器［10～13］设计的控制系统结构图如图4所示。

由图4状态反馈结构图可知引入状态反馈后系统控制规律为

其中k=[ ]k1k2k3为状态反馈增益矩阵。

通过二次型性能指标对最优控制器进行设计，其性能指标函数表达式为

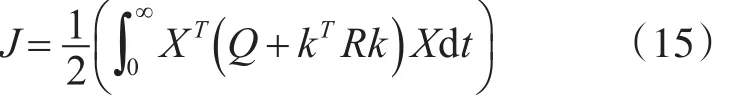
由于控制系统闭环稳定，所以当t趋近于无穷时，X(t)趋向于0；对其微分可得：

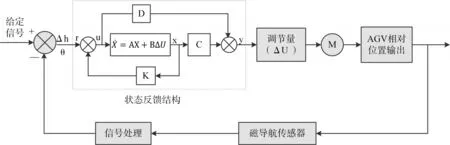
图4 控制系统结构图

令k=R-1BTP代 入 式 （17） 可 得 ：=0为（Riccati）黎卡堤方程，P为方程的解。

由上述证明可知最优反馈增益矩阵k完全由P确定，在实际计算中一般取Q、R为对角矩阵，利用Matlab中lqr函数：可求出LQR设计的控制器数学模型为

5 系统仿真分析

通过Matlab［14］对上述设计的LQR控制器进行仿真设计，假设AGV初始运行状态时存在偏差为，可得到如图5所示的初始偏差响应曲线，曲线显示通过LQR控制器会调节系统收敛至平衡状态。为观察AGV的三个运行状态量对AGV纠偏能力的影响，分别设初始状态为，通过仿真可得相应曲线如图6所示。

图5 初始偏差综合仿真结果

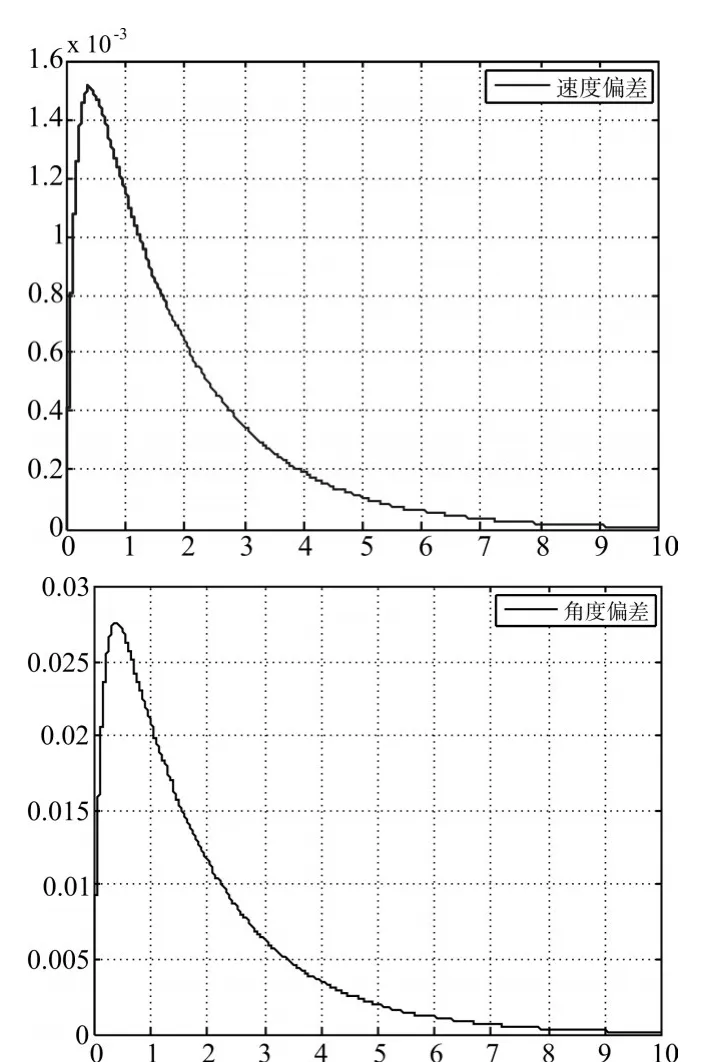
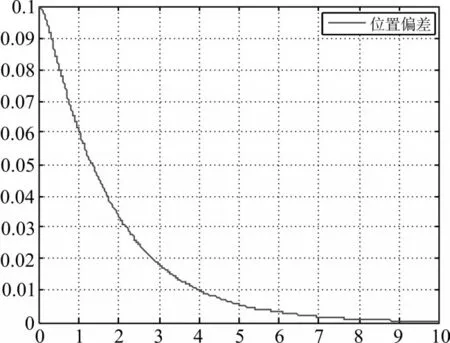
图6 初始偏差单一仿真

由仿真曲线对比分析可知三个偏差均导致AGV偏离磁条，但位置偏差对LQR控制器的影响最灵敏，需要快速纠偏，这一点符合设计思路，AGV发生偏移时磁导航传感器采集信号，使能控制芯片进行纠偏计算。因此在设计控制器时需要调节配置LQR的控制矩阵系数对灵敏度较强的状态量快速调整，从而使AGV快速处于平稳运行状态。

图7 不同Q影响偏差响应曲线

LQR最优控制即使得性能指标J取得极小值，J的大小取决于状态矩阵Q和控制矩阵R。因此在假定初始状态不变的条件下，通过改变矩阵Q和R的值观察参数对系统输出响应曲线的影响，其中Q矩阵的q1，q2，q3分别关联系统状态变量矩阵的三个参数ΔV，θ，Δh，是控制器对系统状态误差的控制，其仿真分析结果如图7所示。

由图7可知q1，q2，q3的变化影响系统响应曲线收敛时间及静差变化，其中q1，q2，q3均越小，静差越小，响应时间也同时变小；q1越大，静差越大，响应时间越大；而q2越大，静差越小，但是系统的响应速度随q2增大而变慢；q3越大则静差和响应时间均越小。因此，选取状态加权矩阵参数时，q1，q2应当都选择小于1的值，而q3尽可能的大。所以参数值的选择应由静差的大小与响应速度的快慢而调整。通过大量仿真对比Q取值如图8中值可达到最佳控制效果。

6 PID与LQR控制仿真对比

通过上述研究找到相对优越的QR矩阵，运用simulink［15］对系统控制结构块进行设计，得到如图9所示的仿真模型。

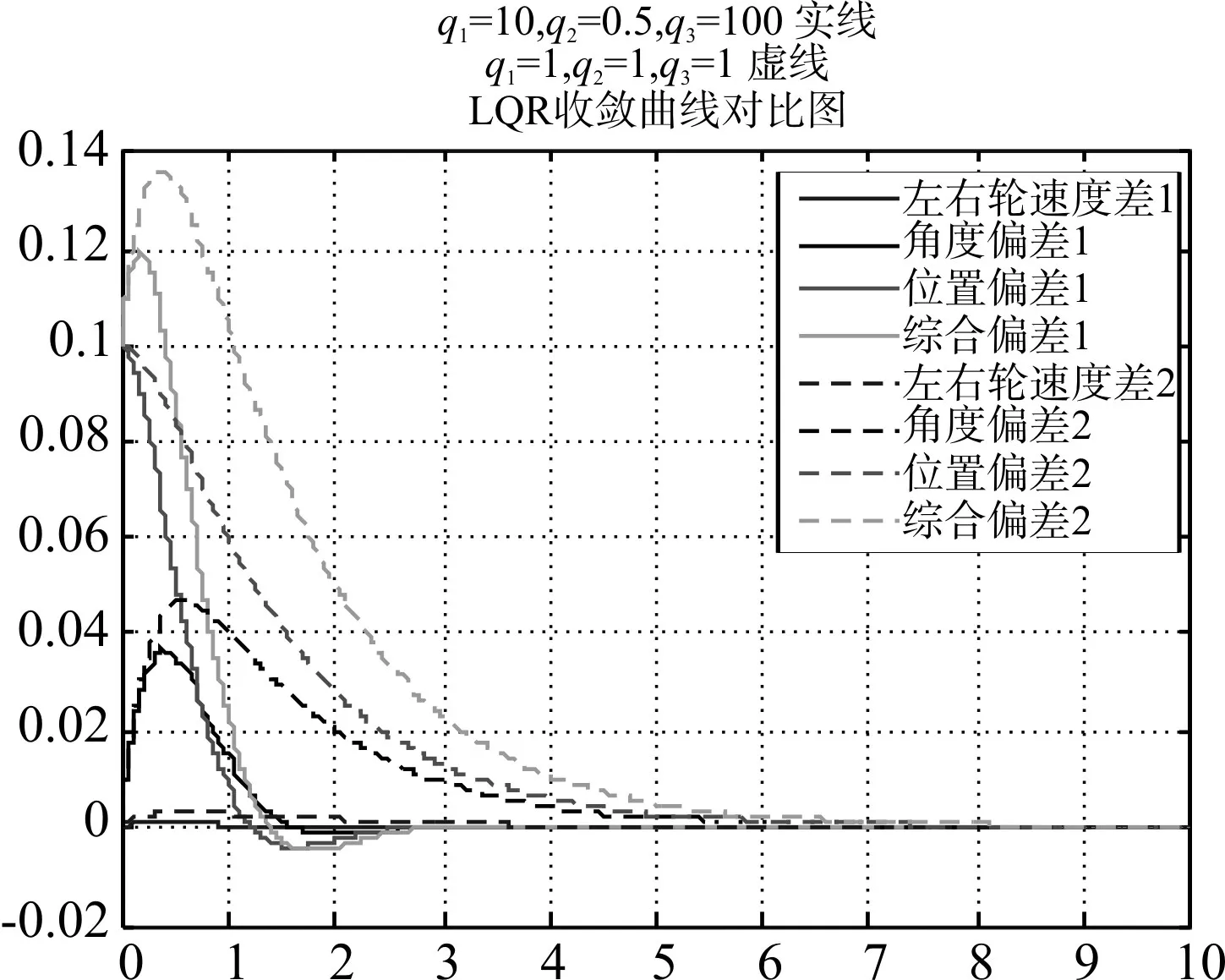
图8 最佳Q偏差响应曲线

仿真运行得到如图10所示的曲线收敛对比图，从图中可以看出AGV在PID和LQR的调整下均可达到稳定状态，但LQR的状态收敛相对较快，同时在静差稳定性方面与PID基本相同，因此说明最优控制器LQR对AGV在纠偏控制过程中具有良好的控制性能。

图9 控制系统仿真模型

图10 PID与LQR收敛曲线对比图

7 结语

本文首先对AGV进行数学建模，建立AGV循迹偏差模型方程，借助实际参数对控制电机线性化处理，建立AGV状态空间模型，并在此基础上设计基于LQR算法的AGV纠偏控制模型，通过Matlab仿真验证模型的可控可观性，通过仿真曲线对比分析其对AGV纠偏控制系统动态性能的影响，找到最佳Q，R矩阵。最后通过Simulink建立LQR和PID控制模型验证表明，LQR纠偏控制模型具有较好的精确性、快速性和平稳性，在工程设计时具有很大的实践意义。