基于拓扑优化和形状优化的桨叶结构设计
2020-03-04周丞林杰刘勇
周丞,林杰,刘勇
(南京航空航天大学 直升机旋翼动力学国家级重点实验室,南京 210016)
0 引 言
直升机与固定翼飞机不同,它由旋翼提供升力和前飞所需拉力,在前飞时旋翼处在复杂周期变化的气动环境中[1]。旋翼是直升机关键的部件之一,对直升机的整体性能有巨大影响。传统的旋翼桨叶结构设计在很大程度上是依赖于设计人员的经验,性能差异明显,通常得不到最优的设计构型。目前,旋翼桨叶结构设计大多是基于固定的桨叶剖面构型,以桨叶的剖面结构参数为设计变量展开优化设计[2-3],导致桨叶减重设计面临巨大挑战。
拓扑优化和形状优化技术广泛应用于固定翼飞机结构设计中。王伟等[4]对某型大展弦比复合材料飞翼结构进行形状与尺寸综合优化设计,实现减重并改善应力水平;董瑞星[5]基于MSC.Patran和Matlab平台进行二次开发,对机翼翼肋进行拓扑优化,在满足稳定性的前提下,节约材料23.2%;张碧辉等[6]基于双向渐进结构优化方法,提出一种太阳能飞机二维翼肋结构的拓扑优化设计方法;Niels Aage等[7]对波音机翼进行全尺寸拓扑优化,与现有的机翼相比,减重2%~5%。但在直升机旋翼结构设计方面,梁剖面拓扑优化最早是Yoon Young Kim等[8]提出的,大多以刚度或者柔度为优化目标,以面积或材料用量为约束条件建立比较优化模型[9],不涉及强度约束,而且没有考虑后续的形状优化。赵志敏[10]对桨毂柔性梁扭转功能段的截面优化,其设计目标为最小化扭转刚度;沈赛男[11]采用有限元法和类似于变密度法的拓扑优化设计方法,以剖面刚度为约束及目标,集成有限元软件、梁剖面特性分析软件以及优化软件实现无铰旋翼柔性梁剖面构型优化设计;任毅如等[12]提出基于变密度法的直升机旋翼桨叶剖面拓扑优化设计方法,以梁柔度或者剖面刚度为设计目标,质量为约束。
拓扑优化和形状优化用于结构优化设计的不同阶段。拓扑优化技术应用于概念设计阶段,用来确定一个最佳载荷传递路径的桨叶结构设计方案,当采用拓扑优化技术确定结构的拓扑构型后,再进行形状优化,对现有构型的CAD设计进行调整优化。桨叶结构设计大多单独采用形状优化技术或者尺寸优化技术,并没有从源头开始设计。因此,本文把拓扑优化和形状优化两级优化方法引入到旋翼桨叶剖面结构设计中,以减重为设计目标,把应力与节点位移作为约束,建立优化模型。第一级优化采用拓扑优化技术得到基本的桨叶构型,在此构型上进行第二级优化,采用形状优化技术,进行局部调整。
1 优化模型
1.1 优化流程
结构优化设计包括三方面:设计变量、目标函数以及约束条件。优化数学模型为
minf(X)=f(x1,x2,…,xn)
(1)
s.t.H(X)≤0 (h=1,2,…,n)
G(X)≤0 (g=1,2,…,n)
式中:X=(x1,x2,…,xn),为设计变量,比如单元的密度;f(X)为设计目标,比如体积或者质量最小化;H(X)和G(X)为响应约束,比如应力水平和位移。
采用数学规划方法,通过求解灵敏度构造近似显示模型,采用小步长迭代找到最优解[13]。当连续两次迭代的目标值的差值小于给定收敛容差时,该优化求解完成收敛。收敛容差默认值为0.005。具体的优化流程如图1所示。

图1 优化流程
本文采用两种优化技术,包括拓扑优化技术和形状优化技术。第一级优化中,拓扑优化的材料插值方法为变密度法(SIMP)[14],即把模型离散的每个单元的“单元密度”作为设计变量,在0和1之间连续取值。优化后,保留单元密度靠近1的区域,删除单元密度靠近0的区域,实现材料在传力路径当中的最佳分配。第二级优化是形状优化技术,基于手工实现网格变形的形状优化技术和基于边界节点自由变形的自由形状优化技术[13],在原有的模型网格基础上通过移动网格节点来高效优化几何形状,提高整体的力学性能。形状优化技术可以提供细节优化处理,无需重新划分网格,节约操作时间。
1.2 设计灵敏度
设计灵敏度是响应优化变量的偏导数。直接法求解适用于形状优化。
有限元方程:
KU=P
(2)
两边对设计变量X求偏导数:
(3)
则对位移向量U的偏导数为
(4)
设计响应一般是位移向量U的函数:
g=QTU
(5)
故设计响应对设计变量的偏导数为
(6)
对于拓扑优化,在计算灵敏度的时候,采用伴随变量法。引入伴随变量E,使其满足
KE=Q
(7)
(8)
式中:K为刚度矩阵;U为单元位移向量;P为单元载荷向量;g为约束函数;Q为伴随载荷向量。
2 拓扑优化技术
直升机旋翼桨叶结构展弦比大,一般采用非线性一维梁整体运动模型加线性的二维剖面模型来处理。本文的优化对象是各向同性的金属桨叶剖面。桨叶剖面形状为多空腔不规则形状。
给桨叶内部(除中心孔外)全部填充材料,作为初始方案。建立桨叶几何模型,如图2所示。选用壳单元来模拟桨叶二维结构,并通过截面属性来定义壳单元的厚度。与实体模型相比,其网格数量会大幅减少,缩短优化的时间。将桨叶模型分为设计区域和非设计区域。桨叶的气动外形和中心孔的形状保持不变,故上下蒙皮和中心孔为非设计区域,其余内腔区域均作为设计区域。

图2 桨叶几何模型
离散的网格以四边形单元为主,允许少量的区域是三角形单元。考虑网格的经济适用性,桨叶模型单元数量为9 161个,节点数量为9 454个。最小成员尺寸要大于三倍的单元平均尺寸。施加最小成员尺寸约束可以消除优化结果中细小的传力路径,得到比较均匀的材料分布。分别设置最小成员尺寸为1.5和1.0 mm时的拓扑优化构型如图3~图4所示。

图3 设置最小成员尺寸为1.5 mm时的拓扑优化构型

图4 设置最小成员尺寸为1.0 mm时的拓扑优化构型
从图3~图4可以看出:在网格数量确定后,最小成员尺寸越小,传力路径分叉越多,应力分布越不稳定。
同时,最大成员尺寸要大于两倍的最小成员尺寸,以防止优化过程中材料的堆积。根据划分的网格单元大小,确定选用最大成员尺寸为4 mm,最小成员尺寸为2 mm。
壳单元所用的材料是铸造铝合金AlSi10Mg,其具有良好的工艺性,密度低,抗腐蚀性好,在航空领域广泛应用。材料特性如表1所示。

表1 AlSi10Mg材料特性
通过Rigid刚性单元对中心孔施加位移约束,Reb3柔性单元定义桨叶剖面载荷的施加位置。
直升机的飞行状态包括超扭、超转、水平飞行、螺旋转弯、自转等。特定展向和周向位置桨叶剖面的载荷在不同的飞行状态下是不一样的。通过动力学综合分析软件CAMRAD Ⅱ对某小型跷跷板构型的直升机在水平前飞80 km/h状态下的旋翼载荷计算分析,得到某个桨叶剖面的载荷,包括挥-摆-扭力矩、径向力、弦向力及垂向力,具体数据如表2所示。
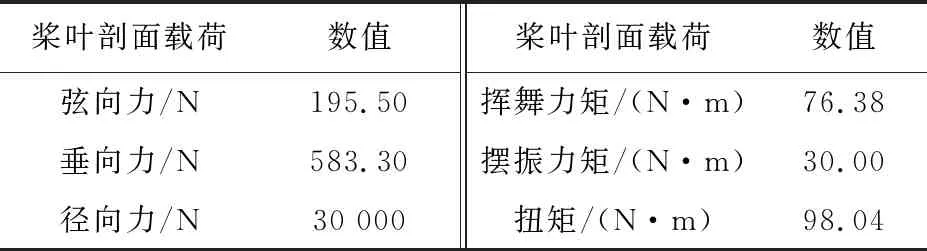
表2 桨叶剖面的载荷
将有限元模型的单元相对密度作为设计变量,约束条件为最大Von mises应力不超过230 MPa且最大节点位移小于1.5 mm,优化目标为桨叶的体积最小化。目标函数迭代曲线如图5所示。

图5 目标函数迭代曲线
从图5可以看出:经过72次优化迭代求解,目标量收敛。
拓扑优化后的模型、动画及应力应变云图等都可以在HyperView[15]可视化环境查看。拓扑优化后的模型如图6所示。

图6 拓扑优化后的模型
Fig.6 Topology optimized model
从图6可以看出:桨叶前端传力路径清晰,呈现几乎正交斜置的网格路径,是主要承受载荷的区域;桨叶中段出现“Z”形样式的结构,对提高桨叶的抗扭刚度产生重要影响;桨叶尾端呈现折线形的结构,可以用来调节摆振刚度。传力路径之外的区域,单元密度接近于0,在重构时删除。设定value=0.505,删除中间密度单元,保留主要的承力结构。
通过OSSmooth模块,导出STEP格式的文件。拓扑优化后的模型边缘有锯齿状、有不连续的结构,需要重构。基于三维建模软件,用样条曲线和直线重构桨叶的中心孔、蒙皮、支撑杆及垫块,如图7所示。

图7 桨叶剖面重构图
对重构后的模型和拓扑优化后的模型分别进行受力分析,最大Von mises应力误差为-2.140%。从工程设计的角度来看,重构对结构性能的影响可以忽略。拓扑优化后,采用形状优化对桨叶模型进行参数化建模及细化处理。
3 形状优化技术
3.1 自由形状优化技术
重构结构的应力分布如图8所示。

图8 重构结构的应力分布
从图8可以看出:桨叶在中心孔附近和腹腔中段出现局部应力集中,且最大Von mises应力为233.9 MPa,超过了材料的屈服强度。
基于重构桨叶的有限元模型,对应力集中的区域细化网格,进行自由形状优化。选择应力集中区域对应的边界节点位置的集合为设计变量,其扰动变形范围由软件自动控制,设置最大Von mises应力小于230 MPa为优化约束,体积最小化为优化目标,通过OptiStruct优化求解。
优化后的形状变量变形云图如图9所示,节点最大移动量为1.015 mm,体积为63 955.671 mm3。
优化后结构的应力分布情况如图10所示。最大Von mises应力降至211.5 MPa,应力分布趋于平缓,支撑杆和垫块部件的应力值比较小,表明还有优化余地。保留本次优化后的网格信息。

图9 形状变量的变形

图10 自由形状优化后结构的应力分布
3.2 基于人工驱动网格变形的形状优化技术
根据合理的设计空间域以及设计者的工程经验,基于人工驱动网格变形的形状优化技术允许网格节点在有限空间内移动,满足设计要求后,确定最佳的变形位置。直接在自由形状优化后的网格信息基础上,采用映射到线几何的方式来定义设计变量,如图11所示,支撑杆i的厚度为bi(i为正整数,1≤i≤15),紧贴上翼面垫块的厚度为h1,紧贴下翼面的垫块的厚度为h2。定义支撑杆和垫块的厚度为设计变量,约束为最大Von mises应力不超过230 MPa和模型最大节点位移小于1.5 mm,优化目标为模型的体积最小化。

图11 设计变量
经过形状优化迭代求解,得到网格分布的最佳位置。形状优化后的形状变量变形如图12所示。
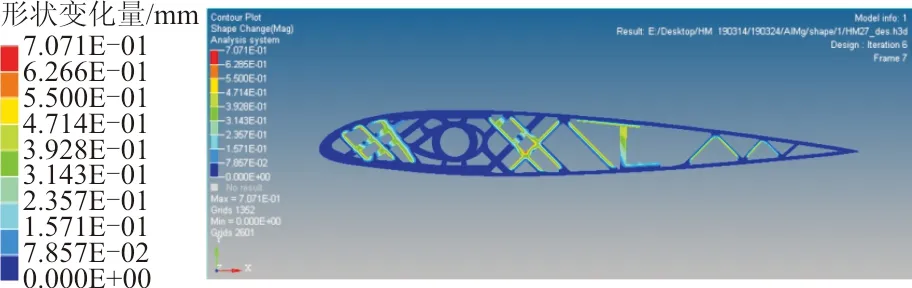
图12 形状优化后的形状变量变形
从图12可以看出:支撑杆和垫块的网格节点的位置集合发生不同程度的变化,其中支撑杆6和支撑杆7发生最大形状变化,数值为0.707 1 mm。
形状优化后的结构应力分布情况如图13所示,可以看出:相比较自由形状优化后的结果,最大Von mises应力略微上升至215.2 MPa,增大了1.749%,仍满足屈服强度。

图13 形状优化后的结构的应力分布
优化后体积为603 953.56 mm3,减少了5.566 5%,如图14所示,模型节点最大位移为1.239 mm。桨叶一阶屈曲云图如图15所示,屈曲因子为6.196 76,大于1,表示桨叶没有失稳。

图14 形状优化后结构的节点位移

图15 形状优化后屈曲一阶图
4 优化结果分析
已知桨叶的气动外形,即在确定的设计空间内,通过拓扑优化找到合理的材料分布路径。相比较初始的方案,重构后模型体积下降50.790%,最大Von mises应力增大了142.32 MPa。在重构的桨叶模型基础上,驱动有限元网格节点变形进行形状优化。与拓扑优化后的重构模型相比,形状优化后的桨叶体积减少了5.117%,最大Von mises应力下降7.99%,局部集中应力的情况有所改善,材料得到了更加高效地使用。
优化前后的数据对比如表3所示。

表3 优化前后的数据对比
体积和应力的变化趋势分别如图16~图17所示,可以看出:最终方案和初始方案对比,桨叶结构减重53.508%,应力上升123.62 MPa,但仍然满足设计需求。
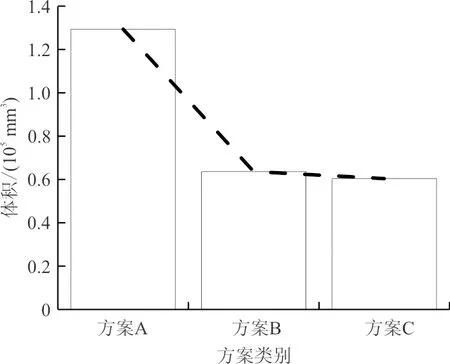
图16 体积变化趋势

图17 最大Von mises应力变化趋势
通过拓扑优化和形状优化,桨叶满足强度和稳定性的要求,几何模型如图18所示。
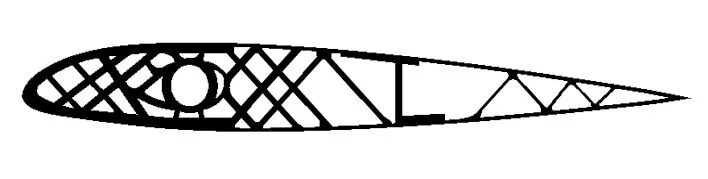
图18 优化后桨叶结构
5 结 论
(1) 在网格数量确定后,最小成员尺寸越小,桨叶内部结构的传力路径分叉越多,应力分布越不稳定。结合划分的网格尺寸和工程设计经验,找到合适的最小成员尺寸和最大成员尺寸的组合。
(2) 通过第一级拓扑优化找到清晰的桨叶内腔的材料分布结构,包括斜置的网状结构、“Z”形结构和后缘的折线形结构。
(3) 通过第二级形状优化,能降低局部应力,找到合理的边界节点位置,确定桨叶几何构型。
(4) 对拓扑优化和形状优化后的模型进行有限元分析,最终桨叶结构满足强度和稳定性的要求,证明基于拓扑优化和形状优化的桨叶结构设计的方法是可行的,为金属桨叶设计提供了借鉴和参考。
