基于Bi-LSTM的无人机轨迹预测模型及仿真
2020-03-04杨任农岳龙飞宋敏曹晓剑王新
杨任农,岳龙飞,宋敏,曹晓剑,王新
(1.空军工程大学 空管领航学院,西安 710051)
(2.中国人民解放军94563部队,威海 264411)
0 引 言
无人机轨迹预测是无人机自主防撞决策中的关键问题。随着无人机的迅速发展,其在军事领域和民用领域所承担的任务日益增加,自主防撞问题也日益凸显[1-2]。如何通过已知信息,动态、准确地预测入侵者无人机在下一个时刻的位置,从而实现自主避让,减少非战斗损失,是自主防撞轨迹预测研究的重点。
轨迹预测的本质就是对时间序列数据的预测,具有高度非线性和时变性[3]。针对轨迹预测问题,目前主要有两种方法:模型化方法和数据化方法。在模型化方法中,T.Baklacioglu等[4]提出了基于遗传算法的运输机爬升和下降轨迹预测模型;汤新民等[5]基于航空器动力学模型,建立了时变混杂系统模型来预测航空器轨迹,可以准确快速地实现航迹推测;乔少杰等[6]提出基于卡尔曼滤波的动态轨迹预测算法,预测精度较高。这种方法对模型准确度要求较高,在飞行轨迹相对简单稳定时有较高的预测精度,但是对于复杂模型的预测精度相对较低。在数据化方法中,杨任农等[7]建立基于NARX反馈神经网络的飞机飞行性能模型,预测结果和收敛速度较好;谭伟等[8]运用遗传算法优化神经网络权重和结构参数,建立BP神经网络机动目标预测模型,预测精度较高;王俭臣等[9]通过改进粒子群算法和梯度法优化Elman网络权重,对无人机降落轨迹进行预测,模型收敛性能较好。这种方法的优点是不用建立飞机运动模型,不考虑运动细节,单纯从数据角度出发,运用机器学习算法去挖掘数据背后的飞机运动规律。但模型输入简单,“学到的规律”不深,不能进行长期稳定的预测。
考虑到无人机在飞行中重量、推力、阻力等时变参数的不稳定性,难以建立精确的运动模型进行轨迹预测。同时,传统数据化方法在轨迹预测时,用到数据量较少,并未考虑到我方位置、姿态对入侵者无人机轨迹的影响,难以准确学习受多种因素影响的无人机运动规律,导致轨迹预测精度不高。双向长短期记忆(Bidirectional Long Short Term Memory,简称Bi-LSTM)[10]神经网络是近年来应用比较多的一种深度神经网络,由于神经网络强大的非线性逼近能力,再结合其特殊的双向循环结构能够更好地学习前向和后向数据中所包含的信息,因此非常适合处理时间序列问题。
因此,本文采用数据化的思路,将轨迹预测问题看作时间序列数据的预测问题,建立基于Bi-LSTM的轨迹预测模型,并将入侵者无人机位置、姿态和两机的相对信息同时输入,对入侵者下一时刻的位置进行预测。
1 问题描述
在实际飞行中,无人机的轨迹受自身、战场环境、敌方机动等多种因素影响。根据专家经验,归纳得到无人机轨迹具有连续性、时序性、交互性三个特点[11]。
①连续性是指无人机轨迹是连续变化的,而不是间断的。
②时序性是指轨迹数据是带有时间性质的,且后一个时刻的位置与前一个时刻的位置是有关的,所以轨迹数据本质上是一个时间序列数据。
③交互性是指自主避障时,多机之间是动态变化的复杂过程,一架无人机的机动会影响另一架无人机的机动,一架无人机的位置也会影响另一架无人机的位置。
因此,在进行轨迹预测时,除了考虑入侵者的位置(x,y,z)、姿态(航向角φ,俯仰角θ,滚转角γ)、速度v外,由于交互性,还要考虑两机相对距离d、相对高度Δh、速度矢量夹角α[12]。
无人机自主防撞示意图如图1所示,可以看出:在xyz坐标系中,当入侵者向另一架无人机俯冲过来时,该无人机做回转避让。无人机知道入侵者t1~tn时刻的位置、姿态、速度和相对信息,就可以对入侵者tn+1时刻的位置进行预测,从而帮助无人机进行避让防撞。因此,轨迹预测问题可以描述为
xtn+1=f(xt1,xt2,…,xtn)
(1)
式中:xti为(xt1,yt1,zt1,φ,θ,γ,v,d,Δh,α),i∈[1,n],即无人机ti时刻在x、y、z方向上的坐标值、航向角、俯仰角、滚转角、速度、两机相对距离、相对高度和速度矢量夹角;xtn+1为tn+1时刻无人机的位置;f为映射关系。
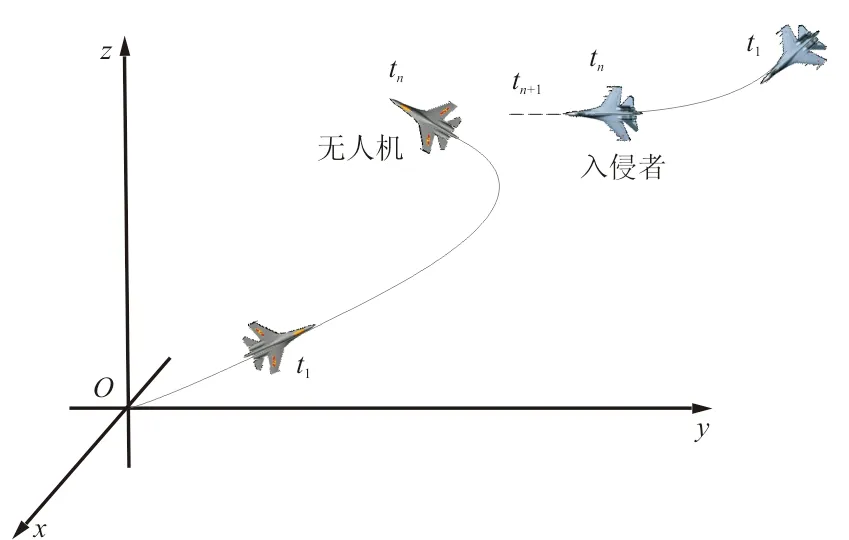
图1 无人机自主防撞示意图
2 基于Bi-LSTM神经网络的飞行轨迹预测建模
2.1 LSTM神经网络模型
LSTM[13]是一种循环神经网络(Recurrent Neural Network,简称RNN)的变体。神经网络本质上是一种非线性函数逼近器,RNN[14-16]是一种带反馈连接的神经网络,由于其隐含层加入反馈结构,即本时刻的输出不仅与本时刻的输入有关,还与上一时刻的输出有关,相当于在时间序列上展开的深度神经网络,使其比较适合处理时间序列数据。因此,RNN常被用于处理上下文包含时序信息的自然语言处理问题。RNN结构如图2所示。

图2 RNN结构示意图
假设输入为xt,隐含层状态为ht,Wx为输入层到隐含层的权重,Wh为隐含层自递归权重,φ为激活函数,则t时刻有
ht=φ(Whht-1+Wxxt)
(2)
ht包含时序变化的信息,即t时刻的输出由t时刻的输入和t-1时刻的输出共同决定。
但RNN存在梯度消失和梯度爆炸的缺点,不能学习长期依赖信息,于是LSTM应运而生。LSTM借鉴人类神经记忆的长短时与遗忘特性,在网络中加入三个控制器,即输入门、输出门、遗忘门,可以学习长期依赖信息,使RNN的性能大幅提升。LSTM常被用于轨迹预测[17]、动作分类[18]和语义分类[19],其结构如图3所示,xt为输入序列;it为输入门;ft为遗忘门;Ot为输出门;ht为隐含层输出;σ为sigmoid激活函数;tanh为tanh激活函数;W为权重矩阵;·为点对乘积。

图3 LSTM结构
根据LSTM结构,得到:
ft=σ(Wxfxt+Whfht-1+bf)
(3)
it=σ(Wxixt+Whiht-1+bi)
(4)
Ot=σ(Wxoxt+Whoht-1+bo)
(5)
(6)
ct=ft·ct-1+it·tanh(Wxcxt+Whcht-1+bc)
(7)
ht=Ot·tanh(ct)
(8)
从式(3)~式(8)可以看出:输入门控制何时让激活状态传入存入单元,即时序数据的写入;输出门控制何时让激活状态传出,即时序数据的输出;忘记门控制全部或部分遗忘,三个门共同完成对数据中规律的学习。
LSTM的优点是使当前单元得到本单元之前所有单元的信息,缺点是无法获得本单元之后的单元的信息[18]。考虑到一组时序数据中,信息不仅包含在过去的数据中,也包含在将来的数据中。如果网络能同时学习前向和后向数据中的规律,就可以进一步提高网络的性能。于是,Bi-LSTM应运而生。
2.2 Bi-LSTM神经网络模型
Bi-LSTM是对LSTM改进形成的一种双向RNN模型。其中,一个Bi-LSTM单元由两个LSTM单元组合而成,一个负责前向信息传递,一个负责后向信息传递,这两部信息组合成最终的输出。Bi-LSTM常被用于文本分类[20]和自然语言处理中,取得了良好的效果。

(9)
(10)
(11)

图4 Bi-LSTM神经元结构
Bi-LSTM网络训练时学习算法采用Adam优化算法[21]。Adam优化算法是深度学习训练中性能最好的算法之一,通过自适应调整学习步长,使得模型收敛速度更快,需要资源更少,学习性能更好,权值更新公式为
(12)
式中:momentum为动量项;v为速度项;E为每次训练后得到的误差和;β1,β2为超参数,一般设置β1=0.9,β2=0.999。
2.3 基于Bi-LSTM的轨迹预测模型
考虑到无人机轨迹的连续性、时序性、交互性特点,结合式(1)可知,可以通过前n个时刻无人机的位置(x,y,z)、航向角φ、俯仰角θ、滚转角γ、速度v、敌我相对距离d、相对高度Δh、速度矢量夹角α共10个量来预测第n+1时刻的轨迹(xtn+1,ytn+1,ztn+1),模型输入输出如图5所示。

图5 Bi-LSTM轨迹预测图
为了提高计算稳定性,将数据归一化处理,输入数据的取值范围纳入[0,1]区间,公式为
(13)
式中:X为某变量的实际值;Xmax为最大值;Xmin为最小值;Y为归一化后的值。
使用训练好的预测模型对预测结果进行反归一化,从而与实际值进行误差比较分析,公式为
X=(Xmax-Xmin)Y+Xmin
(14)
轨迹预测样本数据构建完成后,就可以按照如下步骤建立Bi-LSTM模型进行训练和预测。
Step1从飞机空中训练数据中选择一段飞行轨迹,根据上文构造训练样本和预测样本。
Step2数据预处理,对训练样本和预测样本按照式(13)进行归一化。
Step3把训练样本输入到Bi-LSTM中,改变Bi-LSTM的隐含层节点数,通过最小化输出结果与真实轨迹的误差,确定网络结构。
Step4把预测样本输入到训练好的网络中,得到轨迹预测结果,并进行反归一化。
Step5与其他算法进行对比,分析预测效果。
因此,基于Bi-LSTM的轨迹预测模型算法流程图如图6所示。

图6 算法流程图
3 仿真实验与分析
本文采用离线训练、在线预测的方式,先用大量轨迹数据训练Bi-LSTM神经网络,再用训练后的模型进行轨迹预测,这样输入一组数据的预测时间短,可一定程度上保证模型的实时性。仿真环境为:Intel(R) Core(TM) i5-4590 3.3 GHz处理器,4 GB内存,Windows7 64位操作系统,运行平台为MATLAB 2010a 和JetBrains Pycharm Community Edition 2017.3.3 x64。其中,在Pycharm中搭建基于TensorFlow(深度学习框架)的深度学习环境完成Bi-LSTM仿真。参数设置如表1所示。

表1 参数设置
权重初始化采用截断随机正态分布,将初始化的值控制在两倍的标准差之内,有助于提高计算稳定性。偏差采用均值为0、标准差为1的随机正态分布。学习算法采用Adam优化算法,可以让收敛速度更快,并提高准确率,损失函数采用均方误差函数,公式为
(15)
3.1 轨迹数据选取与处理
本文选取了一段500 s的无人机轨迹数据,共2 000个位置点,并转换到惯性坐标系,如图7所示,前1 800个点作为训练样本,用来训练模型,后200个点作为预测样本,用来进行轨迹预测。为了使实验结果更具说服力,各仿真结果均取30次运行结果的平均值。

图7 飞行轨迹样本图
根据2.3节样本数据构造方法,本文用前8个点预测下1个点,即每次输入1×80的向量,输出1×3的值。这样形成了1 792×80的输入训练样本、1 792×3的输出训练样本、192×80的输入预测样本和192×3的输出训练样本,并按照式(13)、式(14)相应地进行归一化和反归一化。
3.2 隐含层节点数确定
由于神经网络隐含层节点数的确定没有固定的方法,因此采用通试法,从4~15改变隐含层节点数,分析样本均方误差变化来确定,如图8所示。
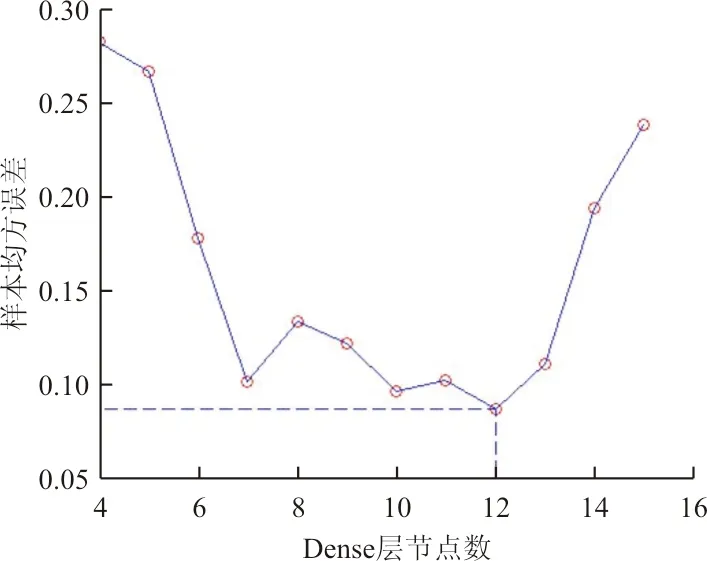
图8 不同隐含层节点数训练结果
从图8可以看出:在隐含层节点数为12时,样本均方误差最小,故隐含层节点数设为12。
3.3 轨迹预测精度对比分析
按照上述参数设置和确定的网络结构,建立Bi-LSTM模型,并建立Elman神经网络模型(设置2个隐含层,隐含层节点数为12,激活函数为Sigmoid)作为对比,分别用训练样本进行网络训练,然后输入预测样本对接下来的200个点进行预测。分别绘制了x、y、z三个方向预测结果及绝对误差(因为基数太大,相对误差都接近0)和三维预测结果,如图9~图10所示。
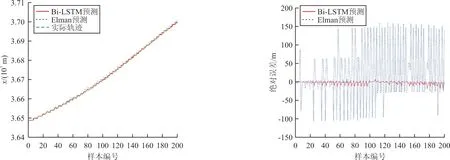
(a)x方向预测结果 (b)x方向预测绝对误差

(c)y方向预测结果 (d)y方向预测绝对误差

(e)z方向预测结果 (f)z方向预测绝对误差
图9 不同方向轨迹预测结果
Fig.9 Trajectory prediction results of different directions

图10 预测结果三维图
从图9可以看出:三个方向上,Bi-LSTM模型预测绝对误差比Elman模型预测误差小,预测结果更稳定。
从图10可以看出:Bi-LSTM模型预测200个点的轨迹与实际轨迹基本重合,误差较小,而Elman模型预测的轨迹误差越来越大。
为作进一步对比分析,对Bi-LSTM和Elman模型预测的200个点的x、y、z三个方向的平均绝对误差进行比较,如表2所示,可以看出:Bi-LSTM模型在三个方向的预测平均绝对误差明显小于Elman模型的预测误差。

表2 Bi-LSTM和Elman模型预测平均绝对误差对比
综上所述,与Elman神经网络预测模型相比,基于Bi-LSTM的轨迹预测模型预测误差更小,精度更高。
4 结 论
(1) 建立了基于Bi-LSTM的轨迹预测模型,通过输入无人机的位置、姿态和两机相对信息离线训练好Bi-LSTM模型,在x、y、z三个方向预测200个点的平均绝对误差不超过4 m。
(2) 与Elman神经网络相比,Bi-LSTM神经网络因其特殊的双向循环结构,可以同时学习过去和未来时刻轨迹数据中的信息,因此具有更高的轨迹预测精度。
