四边简支含多孔材料双层板隔声特性∗
2020-03-03陈亮沈敏
陈 亮 沈 敏
0 引言
由于采用单一的材料进行噪声控制效果并不理想,研究人员对多种材料进行组合设计复合板结构,提高板结构隔声特性[1−2]。在两层平板中间填充多孔吸声材料,在飞机舱室结构中非常普遍。深入探索双层板结构声振耦合系统的物理本质,可以更好地指导高速机车、舰船、飞机、航天飞行器等的声学优化设计[3]。
目前,针对复合板结构隔声特性已有许多相关的研究,总体可分为无限大板和有限大板结构两类。对于无限大含多孔材料复合板结构声振耦合特性,Bolton 等[4]建立了多孔材料与面板的耦合边界条件,理论研究了在双层板中夹层为多孔弹性材料的隔声特性。Liu[5]在Bolton等研究的基础上,研究了含多孔材料的无限大三层板结构的隔声特性。Zhou等[6]考虑了外流场对传声损失的影响。陈卫松等[7]通过传递矩阵法研究了芯层为多孔材料的三层复合板结构隔声特性。Lee 等[8]将板中间的多孔材料作为等效流体,简化了理论模型,计算了双层板结构隔声量(Sound transmission loss,STL)。Yablonik[9]基于声传递理论计算双层铝板中含有多孔材料的复合板STL,使用Johnson-Champoux-Allard 等效模型分析声波在多孔材料中的传播。
实际工程中大多为有限大复合板结构,应当考虑边界条件对结构声振特性的影响。Carneal 等[10]提出用结构模态叠加法表示声场的分布,理论计算了四边简支双层板的STL,并与实验结果对比,验证了其理论结果的正确性。Xin[11−12]等分别研究了简支和固支支撑下中间为空气芯层双层板结构的隔声特性,并讨论了相关结构参数对系统隔声特性的影响。Liu 等[13]研究了四边固支边界条件下,含多孔材料复合双层板结构隔声特性。
然而,对于其他边界条件下,含多孔材料和空气层的复合双层板结构隔声特性的分析尚未见到报道,对于其他边界条件下复合板结构隔声特性研究尚不充分。因此,本文旨在研究四边简支边界条件下,中间芯层为多孔材料和空气层的复合双层板结构的隔声特性。首先基于流体饱和多孔弹性介质的声传播理论(Biot)计算声波在多孔介质中的传播波数;继而采用四边简支边界条件下板结构的模态函数,利用模态叠加法和伽辽金(Galerkin)法推导复合板结构隔声系数理论模型,并数值求解复合板结构STL。将理论模型得到的四边简支复合板STL与实验结果对比,验证理论模型的正确性。最后,详细讨论四边简支边界条件、板结构尺寸和多孔材料主要参数对隔声特性的影响。
1 双层板内衬多孔弹性材料声学模型
1.1 四边简支双层复合板声学模型
双层板由两个各向同性、均质的薄铝板作为面板,中间芯层是弹性多孔材料叠加空气层组成。两个铝板四边为简支边界条件,固定在无限大的刚性声障上。平面简谐波以俯仰角ϕ和方位角θ斜入射到上层面板,如图1所示。上面板的振动通过弹性多孔介质与空气层作用向下传递,引起下面板振动并向外辐射声波。假设由无限大刚性声障隔开的入射声场和透射声场是半无限大的,具有相同的空气密度ρ0、声速c0。结构的尺寸如下:上板和下板具有相同的长宽a和b,上下板的厚度分别是h1和h2,芯层材料总厚度为H。
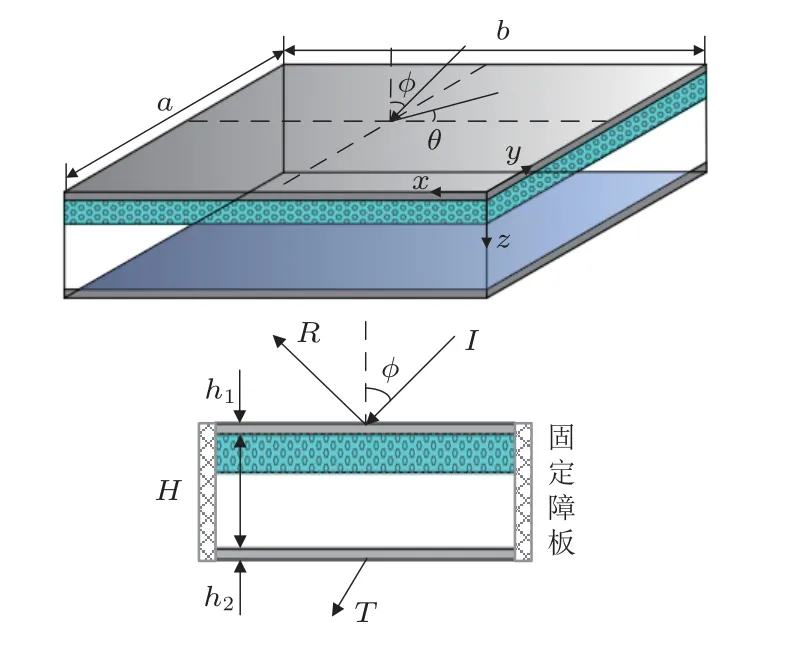
图1 四边简支内衬弹性多孔材料双层板结构Fig.1 A simply supported double-wall sandwich panel lined with poroelastic materials
双层板中间内衬弹性多孔芯层材料或者空气层可以组合成不同的结构,如图2所示。图2中显示的结构AA是指两块面板中间只有空气层;结构BB指的是两块面板都与多孔材料芯层直接绑定在一起;结构BU是第一块板与多孔材料固定,第二块板与多孔材料分离,通过空气层耦合;结构UU是两块面板均与多孔材料分离,通过空气层进行耦合。
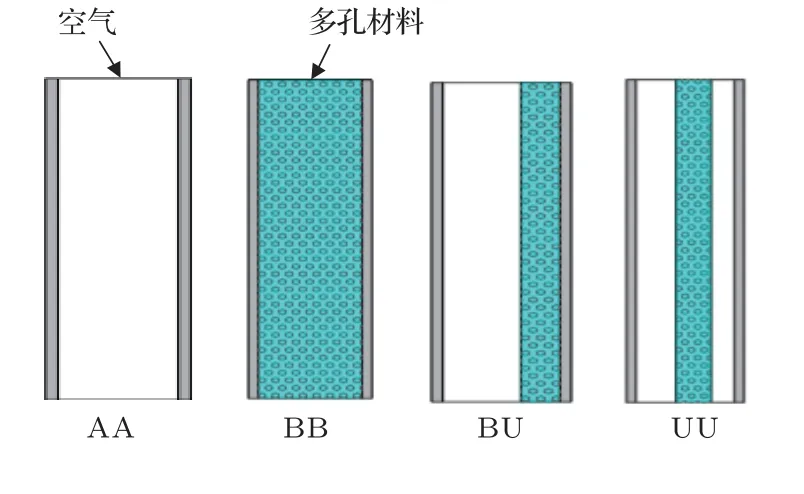
图2 双层复合板不同结构Fig.2 Different configurations of the double-wall sandwich panel
1.2 声波在多孔弹性材料中传播
在给定的入射方向(ϕ,θ)下,平面波入射到上面板,进入多孔弹性介质传播,波数分量为

其中,空气中入射的平面波波数k0=ω/c0。
根据Biot 的理论[14−15],声波在均匀且各向同性的流体饱和多孔弹性介质中传播时,以快纵波、慢纵波和剪切波3 种形式传播。由于接下来的分析中只讨论了声波垂直入射的情况,所以剪切波的影响可以忽视。k1、k2分别为快纵波、慢纵波的波数,具体表达式可参考Biot[14−15]。
利用固相-流体相的体积应变可以推导出位移分量的表达式,固相和流体相中位移在z方向分量表示为
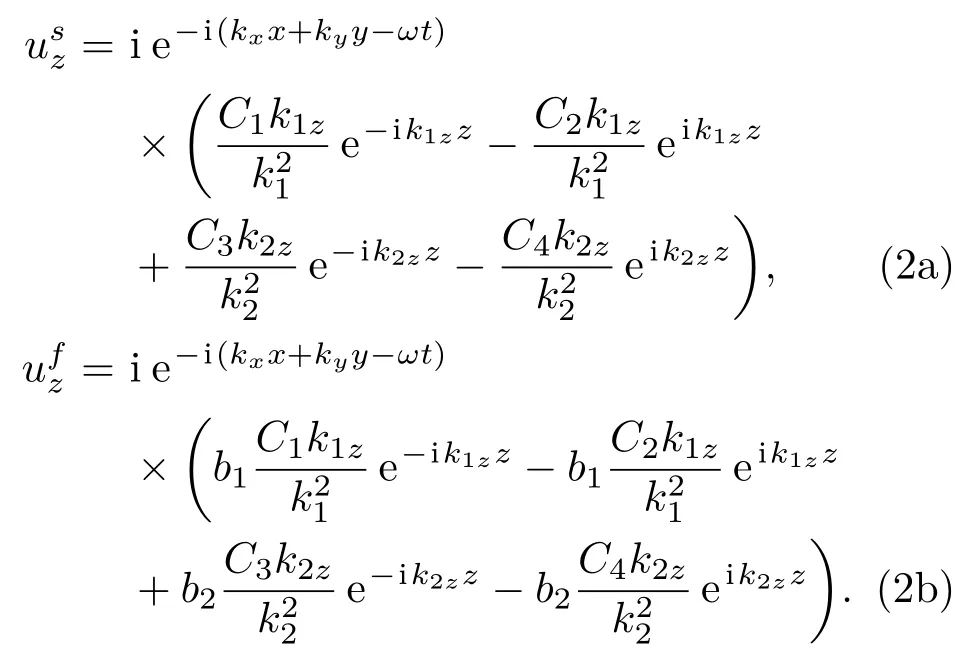
固相和流体相在z方向的应力为


其中:k21,2z=k21,2-(k2x+k2y)为波数在z方向的分量,εs1、εf1、εs2、εf2为与材料参数相关的系数,可参考文献[13]。将在多孔材料固相和流体相中的位移分量usz和ufz、应力σsz和σfz代入复合板结构中多孔材料与面板或者空气层不同耦合界面边界条件求解未知常数C1~C4。
1.3 耦合边界条件
边界条件取决于板和多孔材料的耦合关系,如图3所示。假定面板是各向同性的均匀板,板的厚度对比板的横向尺寸足够薄,根据Kirchhoff-Love 板理论,面内变形以及剪切应力可以忽略。

图3 不同耦合情况Fig.3 Different coupling methods
板与多孔材料直接耦合如图3(a)所示,必须满足3 个边界条件:一个法相应力条件和两个法相位移条件:

多孔材料通过空气层与板耦合如图3(b)所示,在多孔材料表面有3 个边界条件:两个法向应力条件和一个法向速度条件:
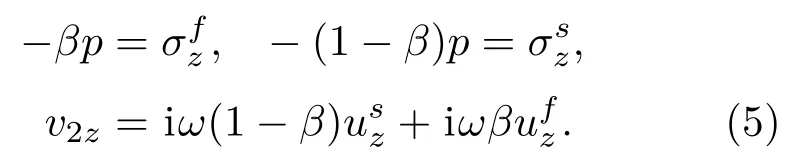
在两层弹性板的表面有两个边界条件:两个法向速度条件:

2 复合板BB布局声振模型
本节详细推导了BB结构的声振问题,由于BU结构、UU 结构推导与BB 结构推导相似,本文将不再赘述。因为是弹性多孔材料直接与面板连接,所以芯层的厚度就是弹性多孔材料的厚度。
2.1 板的弯曲振动
用W1和W2分别表示上板和下板的横向位移。在谐波激励下,上下板的横向变形可以用模态分解形式表达为


对于BB 结构,当两块板都直接与多孔材料固定,上下板的弯曲运动表达式为

其中,双调和算子∇4= (∂2/∂x2+∂2/∂y2)2;板的面密度mi=ρphi(i= 1,2),ρp为板的密度;弯曲刚度,Ep为板的杨氏模量,ηp为板的损失因数,νp为板的泊松比。
2.2 加权余量法
基于权函数的加权余量法,微分方程的解是形函数的线性组合,在整个域内,权函数与微分方程的乘积的积分可以设为0,权函数取形函数ϕmn。对式(9)和式(10)运用加权余量法可得

通过求解积分方程(11)和积分方程(12),可以得
到

其中,矩阵(13)中的元素分别为

方程(11)和方程(12)中只有α1,mn和α2,mn是未知的,m、n取值是无限多的,但是这类方程可用截断方法来进行数值求解:1 ≤m,n≤M,其中最大整数M取值需要同时保证精度高而且计算量小。M2×M2的矩阵∆∗1和∆∗2具体值在附录A中给出。通过求解方程(13)可以计算出模态系数αi,mn(i=1,2),从而能求解出板位移W1和W2。
2.3 复合板结构入射声功率传输损失
入射声场中的声速度势由一个入射波与一个反射波组成,其幅值分别为I和R,声速度势可表示为

假设入射波是单位振幅,即I= 1,同时假设声波透射场是半无限大且消声终止,因此在这个声场中就只有一个振幅为T的透射波,其声速度势可以表示为

将声波入射速度势带入面板和多孔材料以及空气层耦合的边界条件可以分别求出反射系数R和透射系数T的表达式,通过加权余量法求解上板和下板的位移,可以得到反射系数R和透射系数T的具体数值。
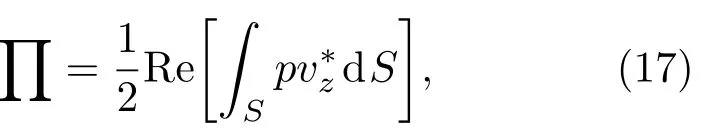
声功率定义为其中,质点速度与声压p的关系为v=p/ρ0c0,上标“*”表示共轭复数。
声波的隔声系数为辐射声功率与入射声功率的比值:

STL定义为:

3 结果与讨论
本节讨论四边简支约束双层复合板隔声特性。考虑到声波垂直入射时,对于四边简支边界条件,可以忽略剪切波的影响,因此,本文仅考虑声波垂直入射下的情况。上下层面板都是铝板,具体参数如表1所示。中间芯层是聚氨酯泡沫多孔材料,详细参数如表2所示。复合板结构可形成4 种不同布局,除特殊声明外,不同布局的芯层材料厚度分布如表3所示。空气密度ρ0= 1.12 kg/m3, 声速c0= 343 m/s,比热比γ= 1.4,普朗特常数Pr=0.71。除特别声明,板尺寸为0.3 m×0.3 m。

表1 铝板性能参数Table 1 Property parameters of the aluminium plates
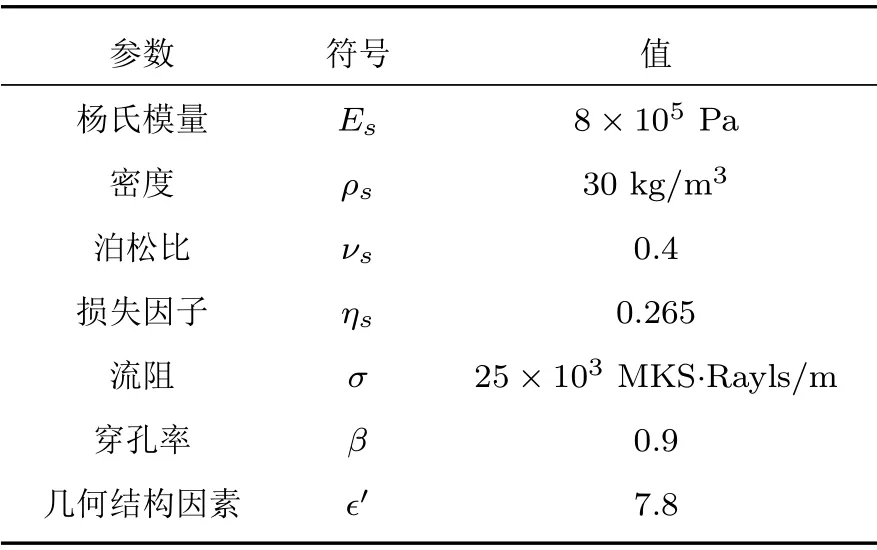
表2 弹性多孔材料性能参数Table 2 Property parameters of the poroelastic material

表3 AA、BB、BU、UU 结构各层厚度Table 3 Layers’ thickness of the AA, BB,BU, UU configurations
3.1 数值结果收敛性检验
由于理论结果是以级数形式出现的,需选取足够的项数保证收敛。通常认为一旦一定项数的级数求和结果在给定的频率下收敛,则该项数的级数求和结果在此频率以下都能收敛[13]。在本次工作中频率10 kHz 用作检验收敛性的最高频率,如图4所示。从图4中可以看出,求解2M2×2M2的矩阵需要级数项数为25,总共1250项结果能收敛。
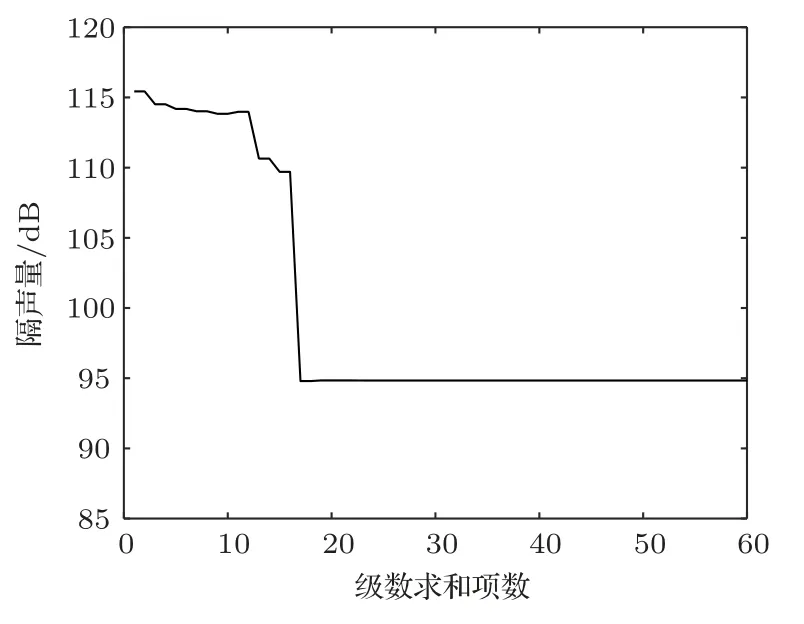
图4 在10 kHz 垂直入射声波激励下,UU 结构传声损失级数解收敛性检验Fig.4 Convergence of double Fourier series solution for STL of UU configuration under the excitation of a normally incident sound at 10 kHz
3.2 模型可行性分析
若将UU 结构中多孔材料厚度设置为0 或者穿孔率设置为1,则UU 结构简化成为AA 结构,即“ 板+空气+板”。铝板尺寸为a= 0.38 m,b= 0.3 m,厚度为h1=h2= 1.6 mm,空气层厚度为H= 48 mm。通过前文推导的理论模型计算得到四边简支AA结构的STL,如图5所示。
图5中显示了本文理论模型计算得到的STL、Carneal等[10]的实验结果、Xin等[12]的理论模型计算得到的AA 结构STL。从图5中可以看到,本文理论模型得到的STL 与Xin 等的理论模型得到的结果、Carneal 等的实验结果都取得了较好的一致性。因为Carneal 等的实验是在固支边界条件下进行的,所以将理论中简支边界条件下板的刚度增加了倍来仿真四边固支的边界条件。为保持一致性,本文做同样处理。

图5 声波垂直入射下传声损失的理论与实验对比Fig.5 Comparison of STL between the current study and experiment under normal incidence
3.3 简支边界条件和固支边界条件对复合板结构STL的影响
图6对比了简支边界条件和固支边界条件下,复合板4 种布局AA、BB、BU、UU 在垂直入射下的STL 曲线。AA 结构在第一个板-空气-板共振频率以后有很多峰值与谷值,这是由气腔里面的驻波共振引起的,但在BB、BU、UU 结构里面这种现象就减弱了,这是因为多孔材料展现了强烈的阻尼效应。一直到3000 Hz,AA、BU、UU 结构的STL 在许多频段都相似。但在3000 Hz 以后,BU 与UU 结构的STL 开始优于AA 结构由于阻尼的影响。在低频段STL 主要受边界条件与板的尺寸影响,所以差别不大。纵观整个频段,就总体隔声性能来看,UU 结构隔声性能最优。
从图6中还可以看出,简支边界条件不仅对AA、BB、BU 和UU 结构在低频范围内的STL 有影响,对于中频和高频的STL 都有明显的影响,但是当频率超过3000 Hz 后,固支和简支边界条件下STL基本一致。简支边界条件下,4种布局板结构第一个“吻合频率”都更靠近低频50 Hz,对比固支边界条件,第一个吻合频率更靠近100 Hz。对于AA结构,简支边界条件隔声曲线中“谷值”明显减少,增加多孔材料后BB、BU、UU 布局复合板结构隔声曲线中出现的“波谷”都比固支边界条件下的要少。在小于80 Hz 频率范围内,固支边界条件复合板结构STL 优于简支边界条件,但是当频率超过80 Hz后,在不同的频率范围内,简支复合板结构STL 大于固支边界复合板STL。
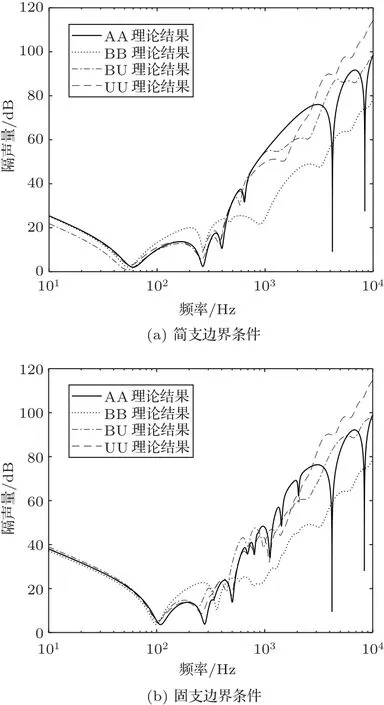
图6 垂直入射下简支边界条件和固支边界条件4种布局复合板结构STLFig.6 Comparison of STL among various panel configurations with simply supported and clamped boundary conditions under normal incidence
3.4 板尺寸的影响
图7中分别显示了在垂直入射下AA、BB、BU、UU四种结构不同尺寸(0.2 m×0.2 m、0.3 m×0.3 m、0.5 m×0.5 m 和无限大)的STL。从图7中可以看出,由于板尺寸与低频声波的波长相比不能被看成无限大,所以除了低频以外,大尺寸的板的STL 都能很好地近似无限大板的STL。并且,随着板的尺寸的增加,无限大板与有限大板的传声损失差别逐渐变小。
从图7中还可以看出在第一个隔声低谷后,由于有限大板的复杂结构模态行为,出现了许多峰值和低谷,并且无限大尺寸还提供了一个STL 渐进极大值。同时在第一个隔声低谷前,可以看到结构的STL对面板的尺寸和简支边界条件很敏感。尽管面板尺寸变化很小,结构的STL 仍变化显著,并且在板尺寸为0.5 m×0.5 m时,隔声曲线就已经接近无限大板了。

图7 AA、BB、BU、UU 结构不同尺寸在垂直入射下传声损失的比较Fig.7 Comparison of STL among various panel dimensions under normal incidence for AA, BB,BU and UU configurations
3.5 多孔材料厚度的变化对STL的影响
图8给出了四边简支AA、BB、BU 和UU 结构在垂直入射下不同厚度的多孔材料层的隔声曲线。计算过程中,板结构参数如表1所示,多孔材料参数如表2所示,3 种布局板结构尺寸都为a=b=0.4 m,BU 结构中空气层厚度为5 mm,UU结构中空气层厚度分别为3 mm。从图8中可以看出,在频率小于200 Hz 时,改变两层面板中间空气层和多孔材料厚度对STL 的影响并不明显;在低频段,板的尺寸和边界条件的影响占主要因素。当频率超过200 Hz,随着两层板中间多孔材料厚度的增加,复合板结构第2 个“吻合频率”逐渐向低频移动,3 种结构的STL 在不同的频率范围内都有明显的增加,BB 结构当频率超过1 kHz 后,STL 明显增大;BU 结构,在200~1000 Hz 范围内,STL 随着多孔材料芯层厚度增加而增加,但是第4 个“吻合频率”随着厚度的增加向低频方向移动,BU 结构高频段STL 反而会减小。4 种布局中UU 结构,第3 个“吻合频率”随着厚度的增加向低频方向移动,当频率超过200 Hz,UU 结构隔声性能在较宽的频率范围内都能达到最优。

图8 多孔材料厚度对AA、BB、BU、UU 四种布局复合结构STL 的影响Fig.8 The effect of poroelastic foam thicknesses among AA, BB, BU, UU configuration under normal incidence
4 结论
本文讨论了垂直入射下四边简支含多孔材料和空气层分层复合板的隔声特性,分析了四边简支边界条件、板的有限尺寸、多孔材料芯层厚度对隔声特性的影响,通过数值结果检验了理论模型的收敛性,并与前人的实验结果对比,理论分析结果与实验结果具有较好的一致性。
研究结果表明,四边简支边界条件与板的有限尺寸对STL 的影响主要在板-空气-板共振的低频段,同时,相比无限大板结构,随着板的尺寸减小,低频的STL 显著提高。在AA、BB、BU、UU 四种结构的隔声曲线中,UU 结构的隔声性能是整个频段上最优的。增加双层板结构中间多孔材料的厚度,4种布局的复合板结构STL 在较宽的频率范围内都有明显的增加,但是随着多孔材料的增加,复合板结构在高频段STL 会降低。因此,对于四边简支复合板隔声性能的声学设计,需要优化设计多孔材料的厚度,在较宽频段内获得更高的STL。
附录A
矩阵表达式如下:
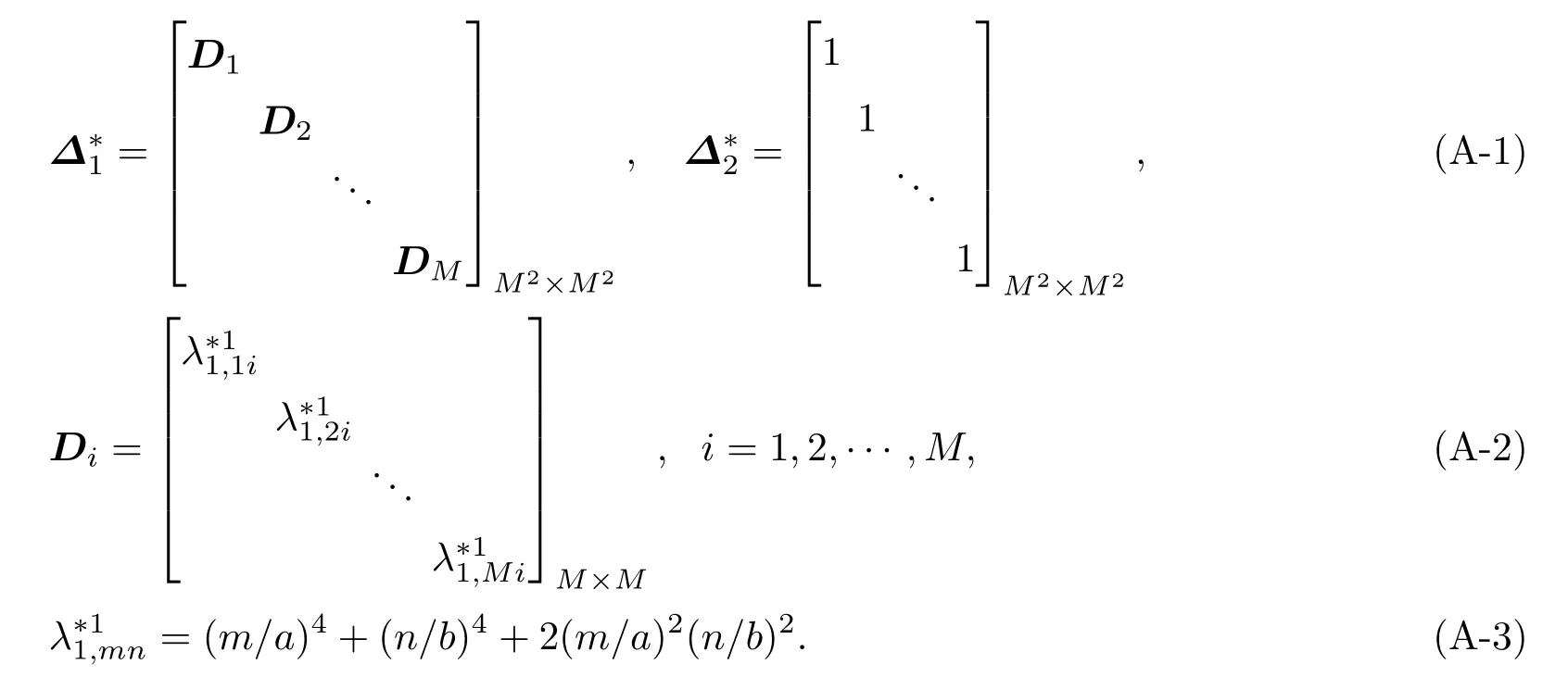
常量fmn(kx,ky)表达如下:

