声子晶体隔声罩的设计与仿真分析
2020-03-03
华南理工大学 机械与汽车工程学院 广州 510640
1 设计背景
噪声存在于各个工业生产领域,长时间反复接触高噪声,会产生健康问题,引起工人心理和生理的变化,从而产生不安全行为。高噪声还会掩盖事故的前兆和危险报警信号,使操作人员听不到报警信号,从而发生工伤事故,影响安全生产。因此,解决噪声问题成为安全生产的关键之一。目前,对噪声控制技术的新探索已成为声学领域的研究热点,国内外许多研究团队针对声衰减和结构振动控制进行了大量研究,促进了新型工程材料和技术的发展,以实现对声响和机械振动的高性能缓解。
声子晶体材料成为近年来声学领域对新型材料探索的成果,其材料结构基于声学超材料设计提出。声子晶体代表一种新的发展方向,是一种人造周期性复合结构材料[1],在保持板材厚度的同时实现了很高的声波传输损耗。这一材料结构本质上由低频谐振结构周期分布组成,对弹性波的传播进行调制,产生声子带隙,即特定频率范围内的声波被禁止通行,抑制声波的传播。声子晶体的这一特性被广泛应用在声学领域,如制作高性能声滤波器、噪声源的减振降噪、制作声隐身衣等[2]。目前声子晶体的研究大多停留在板材层面,在隔声罩的应用中仍很少见。笔者对声子晶体的隔声性能进行研究,研制出针对旋涡风机降噪的声子晶体隔声罩,有效解决工业生产中的噪声问题,提供安全生产所需的声环境。
2 隔声罩原理及性能评价
声波在传递过程中,隔声罩相当于阻碍物。由于声波在空气中的传播阻抗小于隔声罩,介质特性阻抗变大,使一部分声波被阻碍物表面反射回去,一部分声波被阻碍物内部吸收消耗,剩余部分声波穿透阻碍物辐射到另一个空间。
由于反射和吸收作用,使噪声传播的声能降低,这种因阻碍物阻隔声源作用使声能降低的现象称为隔声。隔声罩抑制噪声传播能力的强弱与材料、结构和入射声波频率密不可分[3-4]。
目前,国内针对隔声罩的声波阻隔原理主要依据一维声波方程理论和能量守恒原理进行分析,但由于笔者设计的隔声罩非完全密闭,上述理论对于设有开口的隔声罩研究结果误差很大,因此笔者依据波动声学理论,通过三维线性波动方程进行分析[5-6]。
依据声压的三维波动方程,推导出速度势三维波动方程。
(1)
(2)
Φ和P都是标量,且与质点振动速度V之间存在关系:
(3)
V=-gradΦ
(4)
式中:ρ为介质密度。
将时间变量t和空间变量r进行分离,可得:
Φ(r,t)=T(t)Φ(r)
(5)
式(5)代入式(2),可得:
(6)
式中:T为总动能;n为大于1的整数。
由于速度势Φ是关于t的函数,将式(6)等号两边的常数统一,记为K2,则有:
(7)
(8)
式(8)为亥姆霍兹方程,将其表达为三维声学波动方程的精确解方程,即具有x、y、z参数的形式:
Φ=[Axcos(Kxx)+Bxsin(Kxx)][Aycos(Kyy)+Bysin(Kyy)]
[Azcos(Kzz)+Bzsin(Kzz)](Cejωt+Dejωt)
(9)
式中:Ax、Ay、Az依次为声波在x、y、z正方向上的振动幅度值;Bx、By、Bz依次为声波在x、y、z负方向上的振动幅度值;Kx、Ky、Kz依次为声波在x、y、z方向上的振动波数;ω为声波角频率;C、D为待定常数。
隔声罩的隔声性能评价是研究中最基本的一个环节,通常用隔声量来表示。隔声量是弹性声波穿透隔声罩前后的声能之比,数值越高,表示隔声罩固有的隔声能力越强,也称为传声损失[7]。但在实际应用中,隔声罩的降噪量不同于固有的隔声量,通常采用插入损失来评价隔声罩的降噪性能。插入损失指风机在安装隔声罩前后,在距离风机一定距离的测点处测得的噪声差值。
笔者将旋涡风机作为实际声源,研究声子晶体隔声罩的降噪性能。旋涡风机的体积较小,所设计的隔声罩内部空间相对来说也较小,当隔声罩与旋涡风机辐射噪声表面距离为半波长的整数倍时,容易发生声振耦合,使罩内固有的声场和旋涡风机本身辐射的声功率都发生明显变化[8]。在实际制作过程中,隔声罩壁面需安装吸声材料[9],减少声波的反射,加强声波的吸收,弱化驻波现象,从而忽略加装隔声罩后对旋涡风机本身辐射声功率产生的影响。入射到罩板内表面的声能部分被吸收或透射,此时,隔声罩的插入损失IL为:
(10)

罩壁上的声压P服从牛顿定律,有:
Pi-Po=MdV/dt
(11)
式中:Pi、Po分别为罩壁内、外声压值;M为罩壁单位面积质量。
隔声罩壁边质点的振速如下:
Vz=-∂Φ1/∂z
(12)
式中:Vz为质点振动速度在z方向上的分量。
利用对称性原则,可求出振动波数Kx、Ky。罩壁可以看作是质点集合而成,每个质点处的声压为:
(13)
式中:U0为势能;k为波数;r为半径;s为面积。
可求得安装隔声罩前后罩外某点处的声压值分别为PL、P0,隔声罩的插入损失IL为:
IL=20lg|PL/P0|
(14)
后续笔者通过有限元仿真分析对所设计的隔声罩进行性能评价。
3 隔声罩的设计
3.1 旋涡风机三维结构
笔者以降低旋涡风机的辐射噪声为设计目标,将旋涡风机的噪声源作为声源激励,根据声源特性设计隔声罩[10]。在设计隔声罩时,除了需满足要求的隔声效果外,还需要综合考虑旋涡风机辐射噪声的特性、根据工业标准所需的降噪量、生产制作成本等方面的问题。目前市面上大多数隔声罩的通用性不强,且隔声罩的设计及施工周期较长,成本过高。为满足设备降噪的需求,笔者设计了基于声子晶体的旋涡风机隔声罩。
根据XGB-750型旋涡风机的实际结构尺寸,用Pro/E软件绘制三维结构,便于后续对隔声罩的设计。旋涡风机的三维结构如图1所示。
结合旋涡风机的三维结构,同时以缩短隔声罩的设计周期、降低制作成本、提高通用性为前提,确定隔声罩的外形尺寸,分析旋涡风机的降噪需求,设计隔声罩所需具备的功能,根据不同的功能设计每个壁面。

▲图1 旋涡风机三维结构
3.2 隔声罩外形尺寸
确定目标降噪量后,需要设计隔声罩的外形尺寸,从而确定罩体的框架尺寸。旋涡风机的外形可近似为长方体,因此将隔声罩设计成矩形腔体。旋涡风机与罩壁之间的距离不能过近,避免隔声罩受到旋涡风机的振动激励发生耦合共振,产生驻波频率。应优化壁板结构和形状,提高固有频率,使隔声罩的固有频率避开旋涡风机最高响应频率。
根据标准GB/T 19886—2005《声学 隔声罩和隔声间噪声控制指南》中关于隔声罩尺寸设计的规定,有:
(15)
式中:d为旋涡风机表面距隔声罩外壳的距离;mn为隔声罩壁板材料的面密度;f为壁板传声损失所满足的最低频率。
隔声罩壁板选用外凸型声子晶体结构,确定基体材料为3 mm的均质钢,当隔声罩板只由均质钢制成时,其面密度为体密度与钢材厚度的乘积,即23.55 kg/m2。由于外凸型声子晶体结构在均质钢的表面周期性地附加圆柱振子,因此隔声罩的等效面密度高于23.55 kg/m2。根据旋涡风机的频谱分析结果,已知旋涡风机在80 Hz以下和3 150 Hz以上时,频率响应幅度很低,对整体的噪声值影响不大,所以分析隔声罩在80~3 150 Hz频段的隔声量。隔声罩传声损失所要求的降噪频率最低为80 Hz,将面密度和传声损失所要求的最低频率代入式(15),可得d≥133 mm,即旋涡风机各辐射噪声表面距隔声罩外壳的最短距离为133 mm。由于计算的面密度相对于实际偏低,计算得出的旋涡风机表面距隔声罩外壳的最低距离偏高。由于隔声罩内壁需添加吸声材料,因此对隔声罩的设计需留有一定余量。已知XGB-750型号旋涡风机的规格为300 mm×290 mm×300 mm,则隔声罩外形的尺寸设计为600 mm×600 mm×500 mm。
3.3 功能板块
隔声罩最基本的功能是隔声降噪,首要考虑隔声降噪功能。根据旋涡风机的工作原理,在工作时,空气从进气管进入旋涡风机内部,通过电机的驱动,使泵头内的叶轮高速旋转,使气流变化成旋涡状,叶片的旋转使气流加速,直至通过排气管排出泵体[11],隔声罩设计需要满足旋涡风机进排气管穿管功能。因此,将隔声罩的壁板根据功能不同分两部分设计,即隔声降噪功能和穿管功能。
隔声降噪功能设计的主要核心是阻隔噪声向外辐射。已知旋涡风机的目标降噪量为15 dB(A),针对旋涡风机在200~350 Hz低频段处噪声声压级过高的问题,最终确定将带隙完全覆盖该频段的声子晶体参数用于隔声罩壁板的设计。壁板面除了周期性布置声子晶体局域振子外,还需要对罩内进行消声处理,内壁添置吸声材料,减少声波的反射,加强声波的吸收,弱化驻波现象。隔声罩壁板的材料参数见表1。

表1 隔声罩壁板材料参数
穿管功能主要考虑旋涡风机进排气管穿过隔声罩的开孔设计。由于隔声罩内声能密度很大,罩壁上很小的开孔或者缝隙就能泄漏很大的噪声。旋涡风机正常工作所需的进排气管穿过罩壁时,若采用刚性连接,罩内能量强的噪声源会激励管道与罩壁连接处,产生振动,从而造成二次噪声的传播。为减小刚性连接造成的振动噪声,管口与罩板要采用软连接的方式,使用软橡胶避免声源泄漏。在连接处安装穿管箍口,包裹上柔性密封材料,旋涡风机进气管和排气管的管口外径尺寸都为50 mm,设计穿管功能板的开孔半径为30 mm,安装进排气管时,在圆管周围软连接,包裹上隔声棉[12],起到固定管子、减振和吸声的作用。
严格按照设计的结构参数,应用CATIA软件建立隔声罩的三维模型,如图2所示。图2(a)为隔声罩外部结构,该视图前侧对应旋涡风机的进排气管侧,进风散热板位于驱动电机处,散热气体从罩体顶部的百叶通风板排出。图2(b)为隔声罩的内部结构,罩板的五个内壁面贴附局域振子。
4 仿真分析
应用Virtual Lab软件进行隔声性能的仿真计算,确定声子晶体隔声罩模型的声场计算方法。从声学波动方程推导出亥姆霍兹方程[13],可以用声学有限元法或边界元法进行求解。应用声学有限元法进行求解时,需对整个声场进行离散,适合用于闭合声场。对于开口声场的计算,边界元法更具优势,其原理是依据积分定理,将计算范围由区域转化为边界,由微分方程转化为积分方程[14],且可以同时计算被隔声罩壁板分开的内外两个声场区域,只需提取罩体面网格即可。

▲图2 声子晶体隔声罩三维模型
笔者设计的隔声罩带有开口元素,对于不封闭的网格,选用间接边界元法最为合适。因此,笔者选用边界元法计算隔声罩的透射损失。对隔声量进行分析时,通常采用声振耦合计算,考虑隔声罩的固有频率特性对声场产生的影响,分析类型为基于模态的声振耦合分析,需要建立结构网格和声学表面网格,通过计算隔声罩的结构模态,作为声振耦合计算的振动边界条件,求解罩体的隔声量。
罩体为由五块薄板围成的立方体结构,尺寸为600 mm×600 mm×500 mm。用ANSYS软件进行模型的建立及有限元网格划分,按照设计的隔声罩尺寸与结构,建立一个罩体模型,将隔声罩的底面中心放置在坐标系的原点处,在设计的通风散热部位开口,隔声罩内壁面周期性排列圆柱形共振体。旋涡风机隔声罩在实际应用中,进排气口会通过管道与其它设备进行连接,达到通风换气的目的,进排气口的噪声沿管道传递出去。由于笔者主要目的是研究声子晶体隔声罩的隔声特性,因此模拟时考虑隔声罩板面不开穿管孔。
为了简化计算模型,忽略固定百叶通风板的螺栓,内部局域振子虽然尺寸较小,且对隔声罩的整体结构模态变形影响小,但为了保证后续声子晶体隔声罩声场分析的准确性,将其保留。对隔声罩结构网格划分采用混合网格划分法,将隔声罩分为三个部分进行网格划分,分别是基体板、局域振子和通风散热窗。声子晶体隔声罩结构网格划分如图3所示。整体网格划分完成后,单元总数为79 795,节点数为421 796。
设置隔声罩材料参数,见表2。
设定计算频率范围为80~3 150 Hz,求解得出隔声罩前六阶固有频率,见表3。
经计算得到隔声罩前六阶振型,如图4所示。

▲图3 声子晶体隔声罩结构网格划分

表2 隔声罩材料参数设置

表3 隔声罩前六阶固有频率
由图4可以看出,隔声罩的通风散热窗附近模态振幅较大,因为散热窗相对于罩体其它部位刚度较小,罩内贴附的振子尺寸过小,对隔声罩的整体结构变形没有太大的影响。

▲图4 隔声罩前六阶振型
将计算得到的固有频率数据和结构网格导入声场模块,利用间接边界元法计算隔声罩的隔声量,进行声学网格的划分。间接边界元分析模型的声学网格实际是隔声罩结构的表面网格,由于声学网格不同于结构网格,并不是网格越小精度越高,计算精度由划分的大部分网格形态决定,因此网格尺寸L只需满足:
L≤c/(6fmax)
(16)
式中:c为空气中的声速;fmax为求解的最高频率,fmax=3 150 Hz。
计算得单元网格尺寸最大为18 mm,因此声学网格选用18 mm四方体网格。表面声学网格的划分也分外部罩板、通风散热板和罩体内壁的周期圆柱凸起结构三部分进行,网格外部建立自动匹配层,模拟自由场的声学边界。
进入声学谐波边界元法模块,设置坐标系z轴平行于隔声罩的四个侧面,坐标系原点位于隔声罩底部中心,隔声罩底部设置成反射面,定义障板来模拟硬质地面。假设旋涡风机的噪声源为理想声源,用于旋涡风机噪声源声学仿真,简化后的噪声源可精准求解隔声罩的隔声量。
前处理完成后,进入声学响应操作,使用声振耦合模块进行场点声压分布计算,设置分析频范围率为80~3 150 Hz,频率间隔为50 Hz。计算场点处的声压频率响应函数,定义隔声量为理想激励声源在场点处的声压与该场点声压的差值。图5所示为驱动电机侧、顶部和泵头侧对应场点的传声损失曲线。
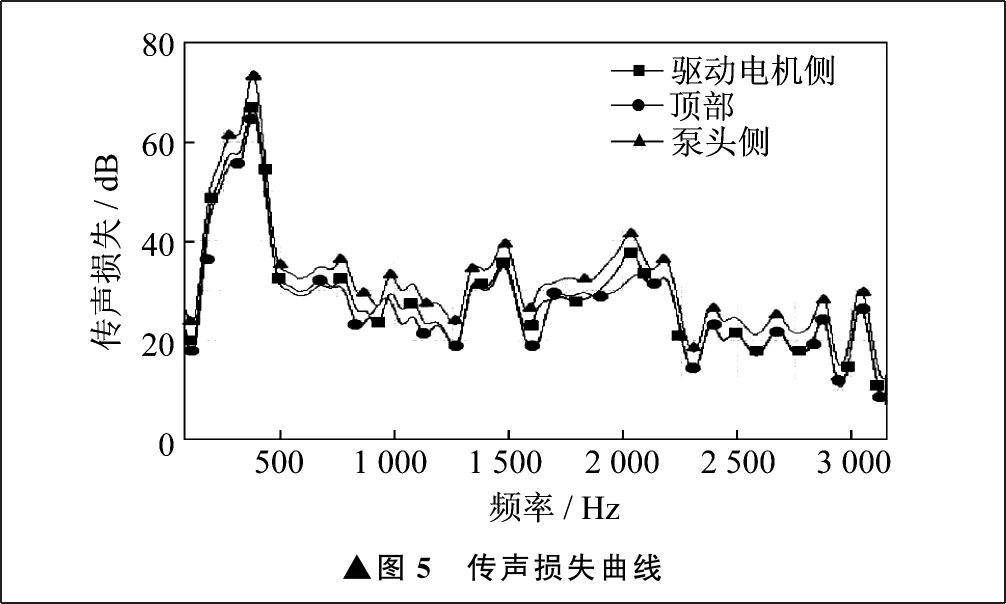
▲图5 传声损失曲线
由图5可以看出,声子晶体隔声罩满足XGB-750型旋涡风机在工业应用中的目标降噪量,且在200~350 Hz低频段处,声子晶体隔声罩出现带隙。在1 500~2 250 Hz中高频段处,出现两个传声损失为40 dB(A)的隔声峰值,符合基体钢板的质量密度定律。通过对隔声罩进行仿真分析,计算得到声子晶体隔声罩的平均隔声量为22.1 dB(A)。
5 结束语
笔者依据旋涡风机的工作原理,对声子晶体隔声罩进行设计和隔声性能的仿真计算。根据旋涡风机在实际工作中的需要,选取最佳降噪材料,基于隔声罩声学模型,应用Virtual Lab Acoustics软件对所设计的隔声罩进行隔声性能的分析,发现声子晶体隔声罩在200~350 Hz低频段处出现带隙特性,在1 500~2 250 Hz中高频段处,出现两个隔声峰值。通过仿真计算得到声子晶体隔声罩的平均隔声量为22.1 dB(A),证明笔者设计的隔声罩在降噪方面符合要求。
