加速度传感器灵敏度计算数学模型及其求解算法
2020-03-03吴发明
吴发明
(厦门乃尔电子有限公司,福建厦门 361000)
0 引言
压电加速度传感器是一种将力学量转换为电学量的检测装置,可用于振动冲击和线加速度的测量,在导弹飞行试验和高速碰撞测试中,均要进行加速度历程测试[1]。对于高温应用场合的压电加速度传感器,由于耐温高的客观条件限制,高温电荷型输出的压电加速度传感器通常采用压电元件堆栈式的轴向压缩型结构,该传感器结构通常在装配成部件后,再通过机加切削调整惯性质量块的重量,最终调整传感器灵敏度至目标值区间内。该方式的组装过程及灵敏度调整较为繁琐且效率低下,此外,传感器易因伴随机加工产生的振动及切削热造成惯性质量块与压电元件间产生相对转动,使压电元件存在碎裂或部件结构内部存有内应力等不良缺陷乃至报废。为解决该问题,提高该结构型式的压电加速度传感器在装配前的灵敏度计算及惯性质量块重量调整的研究十分必要。
1 电荷灵敏度计算数学模型
由于在工程设计采取的措施和高温应用场合的要求,压缩型压电式加速度传感器结构如图1 所示[1-2],由基座、压电元件、导电片、上绝缘片、下绝缘片、惯性质量块、预紧螺母组成。当传感器在被测物体上随被测物运动时,其惯性质量块在加速度的作用下产生惯性力作用在压电元件上,压电元件产生与此作用力成比例的变形,由于压电元件的压电效应,便产生与压电元件形变成比例的电荷。
如图1 所示,对于第i 个压电元件而言,其惯性质量块由质量块、上绝缘片、(i-1)个压电元件、(i-1)个导电片组成。故第i个压电元件所产生的电荷灵敏度为:

因此,压缩型压电式加速度传感器的灵敏度计算表达式为:

式中,mblock为惯性质量块的质量,单位为g;minsulator为绝缘片的质量,单位为g;mcondutor为电极片的质量,单位为g;mp为压电元件的质量,单位为为第i 个压电元件的压电参数,单位为pC/N。
由灵敏度计算表达式可知,实际装配时,若将压电参数值大的压电元件装配在越靠近基座,则传感器灵敏度值越高,反之则越小。

图1 轴向堆栈式压缩结构示意
1.1 灵敏度定义
压缩型压电式加速度传感器灵敏度的数学定义可表示为:

式中,mblock为惯性质量块的质量,minsulator为绝缘片的质量,mcondutor为电极片的质量,mp为压电元件的质量,为第i 个压电元件的压电系数d33。由于实际生产存在差异性,难以保证任意两个压电元件的压电系数d33均相等,即,因此压缩型结构压电加速度传感器所用的n 个压电元件,存在组装顺序约束。压缩型结构压电加速度传感器的灵敏度集可表示为:

该灵敏度集的压电元件的压电参数序列可表示为:

1.2 目标函数
假设某压缩型压电式加速度传感器采用n 个压电元件,其灵敏度期望值为,可接受灵敏度偏差值为。如何合理安排压电元件的组装顺序,使传感器灵敏度最接近其期望值即为灵敏度最优求解问题,则灵敏度集Sv寻优的数学模型为:

1.3 评价函数
为衡量算法迭代新解的优化程度,给定第i 次迭代计算评价函数的数学定义为:

式中,Δgi称为第i 次迭代的函数代价差,为第i 次迭代的初始解为第i 次迭代的新解,g(SPE)为SPE的代价函数。若Δgi<0 或满足Metropolis 概率接受准则[3],则称新解优于初始解
1.4 最优求解
由式(6)可知,传感器灵敏度最优求解问题的主要因素为压电元件的压电参数序列D33和惯性质量块质量mblock的寻优问题。
基于初始质量块的质量mblock,求解得到压电元件的压电参数迭代最优序列,其对应的灵敏度为则压电参数迭代最优序列作为最终最优序列输出;否则,基于压电参数迭代最优序列求解得到惯性质量块的质量
2 算法
2.1 算法流程
对于压电元件数量较多的压缩型压电式加速度传感器灵敏度规划问题,若采用穷举法求解,则计算量随压电元件个数n 呈指数级增长,耗时长且计算效率低。由于模拟退火算法具有全局最优的理论特性[4],本文采用混沌模拟退火算法求解压缩型压电式加速度传感器灵敏度最优规划数学模型,收敛到全局最优解的效率明显比标准模拟退火算法高。
混沌模拟退火算法流程如图2 所示[5],该算法相比标准模拟退火算法,增加了记忆当前最优解的功能、补充了回火升温过程并引入混沌随机序列生成函数,其中:①定义及初始化。定义并初始化冷却进度参数(退火起始温度ts及终止温度te、冷却系数Q 和MapKob 链长MapKobL)、玻尔兹曼常数kB、回火系数At以及新解的接受次数AccecptNum,并选定初始迭代解;②对当前t 和i=1,2,…,MapKobL,重复执行③~⑤;③对当前解混沌随机产生新解;④计算函数代价差Δgi;⑤若Δgi<0,则接受为(i+1)次迭代的初始解;否则计算Metropolis 概率值Accept(Δgi,t)=exp(-Δgi/1.5t),并在闭区间[0,1]上混沌产生随机数randVal,若满足Accept(Δgi,t)>randVal,则否则⑥在次迭代之后,若新解的接受次数AcceptNum 大于预设值,则退火降温;否则回火升温,重新执行②~⑤;⑦若满足迭代终止条件,则输出迭代最优解;否则返回②,继续迭代计算。本文的迭代终止条件为连续3×MapKobl 个迭代新解未被接受或当前温度t≤te;⑧若迭代最优解满足期望偏差条件,则输出压电元件的参数序列迭代最优解,结束程序;否则基于压电元件的参数序列迭代最优解,求解得到惯性质量块的质量,结束程序。
2.2 控制参数
基于混沌模型具有遍历性、初值条件敏感性等特点[6],本文采用一维Logistic 映射的常用混沌模型作为混沌随机序列的生成函数,其数学模型[6]为:


图2 算法流程
其中x∈[0,1],μ∈[0,4],为混沌控制参数。当μ=4,该系统无稳定解,是区间的满映射,呈现完全混沌状态。因此,本文取μ=4。
相关控制参数的具体取值如表1 所示,取值说明:①退火起始温度ts及退火终止温度te。以退火温度t 为混沌随机序列生成的迭代初值,因此t∈[0,1],结合退火过程的充分性及计算效率而确定具体取值;②冷却系数Q。本文采用指数式降温,结合热力学退火过程,为丰富系数Q 的取值、增强算法的适应性并提高迭代计算速度而确定Q 在各个温度区间内的具体取值;③MapKob链长MapKobL。增加算法自适应性,充分退火并提高收敛到全局最优解的可靠程度而确定其具体取值;④波尔兹曼常数kB。依据Metropolis 概率接受准则,提高算法避免陷入局部最优的能力而确定其具体取值;⑤回火系数At。统筹兼顾计算速度及退火充分程度的影响而设定此参数值;⑥新解的接受次数AcceptNum。结合退火充分程度及迭代解优化程度而设定具体取值。
3 算例验证
3.1 测试实例
如图1 所示的轴向堆栈式压缩结构,实际验证的传感器由1 个预紧螺母,1 个质量块,2 个绝缘片,12 个导电片,13 个压电元件和1 个基座组成,具体参数见表2。由此可见,对于压电元件数量较多的压缩型传感器,若采用人工交互方式规划压电元件的装配顺序,效率低且易出错。

表1 算法参数
3.2 验证结果
以VB 语言编写实现,进行30 次实例测试。测试用的电脑配置为双核,CPU 主频3.30 GHz,内存8 GB。针对压缩型传感器压电元件的压电参数序列以D33={20.6,20.1,20.7,20.5,10.2,20.4,10.8,20.2,20.8,10.4,20.3,20.9,10.6}作为初始序列,则初始灵敏度值为67.82 Pc/g。30 次测试的迭代计算结果统计内容包括最大灵敏度最小灵敏度如表3 所示。其中对应的压电元件的压电参数序列={10.2,10.4,10.6,10.8,20.1,20.2,20.3,20.4,20.5,20.6,20.7,20.8,20.9}对应的压电元件的压电参数序列={20.9,20.8,20.7,20.6,20.5,20.4,20.3,20.2,20.1,10.8,10.6,10.4,10.2}。

表2 传感器参数
由表3 计算结果可知,基于当前的压电元件的压电参数序列D33,必须调整惯性质量块的质量方能确保组装后所得的灵敏度满足其期望值及其偏差的要求。惯性质量块的质量调整区间为[20.16,21.90]。
由以上实例验证结果可知,构建的压缩型压电式加速度传感器灵敏度优化规划数学模型及其求解算法,在传感器灵敏度寻优时,具有计算用时少、自动化水平高的特点,优化所得的压电元件装配序列及灵敏度计算结果令人满意,可应用于堆栈式压缩型结构的压电式加速度传感器的实际组装生产指导。
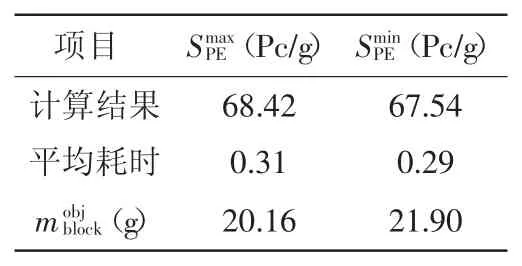
表3 测试结果
4 结论
通过压缩型压电式加速度传感器灵敏度规划的数学模型及其求解算法,建立压缩型PE 加速度传感器灵敏度自动优化方法。通过实例验证结果,表明该方法可解决压缩型压电式加速度传感器组装过程及灵敏度调整较为繁琐费时且效率低的问题。该自动优化方法与实际装配后再通过车削质量块进行减重的传统方法相比,可满足实际装配工艺需求,且具有效率高、寻优质量稳定、可提前预警等优点。
