桂林地区CFG桩复合地基沉降变形研究
2020-03-03莫学芬刘之葵覃晓雨
莫学芬,苏 阳,刘之葵,钟 宣,覃晓雨
(1.桂林理工大学 地球科学学院,广西 桂林 541006;2.桂林理工大学 土木与建筑工程学院,广西 桂林 541004)
0 引言
CFG桩复合地基技术自诞生以来,因其具备施工方便、工期短、造价低、质量易控制,且在对地基的工后沉降以及处理过后的承载性能方面有着极大的改善而广泛地应用在土木工程建设中,并取得了良好的社会经济效益。复合地基沉降计算是复合地基设计与研究的重要问题,复合地基的沉降是一个复杂的综合过程,影响因素很多[1-2]。而国内外众多的学者也对复合地基技术沉降变形方面展开了许多相关研究。Borland M[3]对桩、土作用理论进行研究,若天然地基强度满足了设计要求,而沉降变形却过大,可采用少量的桩来减小沉降达到设计要求。Xu et al[4]采用柔度法研究了桩复合地基的受力特性,提出了一种利用等面积变换技术旋转加载面进行数值积分的新方法用于计算地基土的时变性沉降。傅景辉[5]、池跃君[6]、徐洋[7]、翟建华等[8]都通过对桩、土、垫层三者协同作用关系基础上进行研究分析,并就此提出了各自有关复合地基沉降计算的实用方法。池跃君等[9-10]研究复合地基中应力场的分布规律,对此提出了沉降计算的双层应力法,然而此方法对桩、土及垫层三者之间的协同关系并没有考虑到。杨光华等[11]基于原状土切线模量法,得到了一种计算结果较精准的刚性桩复合地基沉降计算方法,且考虑到桩、土的共同作用和沉降的非线性特性。梅国雄等[12-14]学者根据一维固结理论和土体本构关系在线性或近似线性的加载下,得出地基沉降—时间曲线呈现出“S”型的特性。Hooper[15]、王瑞芳[16]、周爱军[17]、黎寰[18]、范冀哲等[19]利用有限元数值模拟分析对复合地基沉降变形影响因素进行研究,得到减小复合地基沉降的方法。
从以上文献可以发现,对于沉降变形计算方面,现有的研究也不在少数,一些学者针对桩、土、垫层三者协同作用也做了很多研究,但在沉降计算与实践相结合方面依旧与现实存在很大偏差,假定的都是理想条件,与实际相比存在较大的出入。鉴于土体本构模型的复杂性,对于目前的测试方法及设备而言,如何精准测定土中初始应力和参数等依旧是难以做到,因此,在采用一些沉降变形计算方法应用上与试验检测值及工后观测值上还是存在较大偏差。
CFG桩复合地基虽在土木工程建设中得到一定的应用。但CFG桩复合地基的设计方法,特别是沉降计算方法争论比较大。综合来看,目前比较经典的计算沉降的方法有两种,即规范的CFG桩法与双层应力法,本文通过对工程实例的沉降计算,对上述两种计算进行对比分析,并在其基础上提出了一种修正公式。
1 桂林岩溶地区CFG桩基情况
桂林岩溶区常用的几种地基处理方法:换土垫层法、灌填(浆)[20]、桩基法、强夯法、梁板跨越或调整柱距法、CFG桩复合地基[21-22]。CFG桩以其能够充分发挥桩间土的承载力,大幅度提高软弱地基承载力,施工效率高,施工成本低,环保等优点,近些年来,在桂林地区被广泛地推广和应用。其作用机理主要包括桩体作用、挤密作用、桩土约束作用、排水固结作用、褥垫层作用。其在桂林岩溶地区地基处理时具有承载力提高幅度大、可调性强;桩体的排水作用;时间效应;复合地基沉降变形小等工程特性。
2 三种沉降计算方法简述
2.1 规范法
规范法[23]思路是土体分层上,复合土层与天然地基相同,模量大小上,复合模量等于天然地基分层模量的ζ倍,下卧层压缩量依旧按照天然土层计算,其中,采用各向同性均质的直线变形体理论计算加固区和下卧层土体的应力分布,最终复合地基的沉降变形由两者沉降之和乘1个沉降经验系数所得,其计算公式(1):
(1)


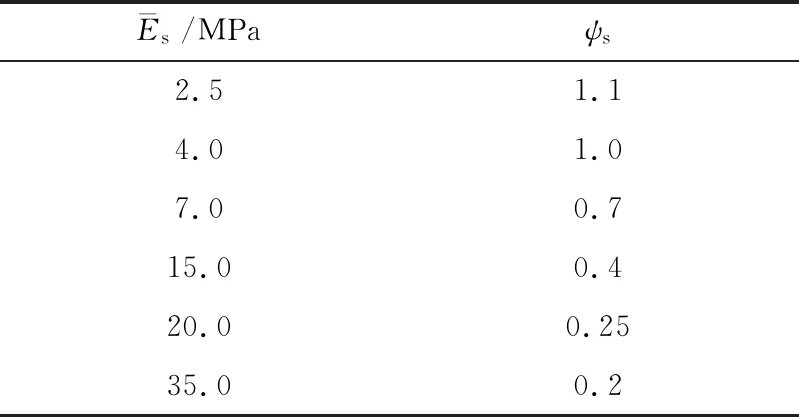
表1 沉降计算经验系数ψsTable 1 Empirical coefficient ψsof settlement calculation
复合地基沉降变形计算深度应符合大于土层的厚度,并按公式(2)计算:
(2)
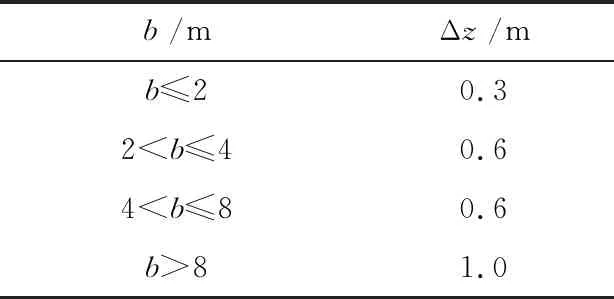
表2 Δz值Table 2 List of Δz value
2.2 双层应力法
池跃君[9]根据CFG桩复合地基实测的土中应力分布,对土层的应力分布进行假设,而土层应力分配比值则通过解析解和数值方法进行计算。对于桩间土顶面及下卧层顶面处应力水平大小通过各种参数条件下的回归经验公式(3)进行求解:

图1 复合地基沉降计算分布示意图Fig.1 Schematic diagram of settlement calculation distribution of composite foundation
(3)
式(3)中:δsr、δss分别为桩间土顶面、下卧层顶面应力水平系数。取值主要依据具体土层土质状况及设计参数确定;若有当地经验,依据当地经验取值;λ为桩间土顶面应力调整系数,一般取值λ=1;B/L为基础的宽度与桩长比;sa/d为桩间距与桩径比;H/d为垫层厚度与桩径比;Es2/Es1为下卧层与加固区压缩模量的当量值之比。
求解δsr、δss值后,可继而求解桩间土顶面附加应力psr值和下卧层顶面附加应力pss值:
(4)
故而最终沉降量的计算公式为
sc=ψ1s1+ψ2s2
(5)
式(5)中:p0为上部结构传至基础底面的平均附加应力;ψ1、ψ2为沉降计算经验系数,取值通常是依据当地沉降观测资料和相关工程经验进行,如果没有地区经验,取值也可依照规范中表格计算,见表1。
2.3 基于规范修正的公式
采用规范法计算沉降变形,加固区顶面和下卧层顶面均以相同的附加应力值计算,对于桩端持力层为良好土层或岩石时,此时下卧层沉降变形较小,主要以加固区为主;此外,基底压力传至下卧层顶面时实际上已远小于加固区顶面应力值,当下卧层依旧采用相同的附加应力值计算,无疑会导致下卧层沉降变形偏大,由此导致最终沉降变形偏大,设计中造成不必要的浪费,增加工程成本。双层应力法是采用数值分析方法回归的经验公式,由试验拟合而来,对于下卧层沉降计算比之规范法更加优越,但此方法难以保证其稳定性且应力水平系数难以准确确定,计算也十分的繁琐,工作量较大,在实际工程中并不适用。对此,本文提出一种基于规范法结合双层应力法的修正公式,即公式(6)。
修正公式在计算过程中,将加固区和下卧层分别计算,加固区依旧按照复合土层模式计算,复合模量等同于天然地基分层模量的ζ倍[23];考虑到基底压力传递至下卧层顶面已大幅度削减,如若依旧按照规范法采用相同附加应力计算必然使结果偏大,故此,下卧层沉降计算采用压力扩散法进行计算,最后借鉴双层应力法思想[9],两部分沉降之和即为最终沉降量。公式(6)即考虑到下卧层沉降变形值,在计算方法上也是浅显易懂,计算量较小,并通过工程案例对其进行验证。计算公式(6):
(6)
式(6)中,pb为下卧层顶面处附加应力值,
(7)
其余参数含义同上所述。
3 工程概况
工程所在地为桂林市雁山区,雁山区全境多为石山和丘陵,具有典型的岩溶地貌特征。以学府雁苑内兴建的32#楼为例展开系列分析,32#楼高6层,场地内素填土①-2层、可塑红黏土③-2层、软塑红黏土③-3层地基承载力达不到设计要求。各土层主要物理力学性质描述见表3。
该工程32#楼2号点CFG桩平面布置见图2;工程地质剖面图见图3。

表3 场地各主要土层物理力学指标Table 3 Physical and mechanical indices of each main soil layer in the site

图2 32#楼2号点CFG桩平面布置图Fig.2 CFG pile layout map of No.2 point of Building 32#

图3 32#楼工程地质剖面图Fig.3 Geological engineering section map of Building 32#
本文以32#楼2号点为例进行分析,计算其最终沉降量,并和实测沉降值进行对比分析,提出建议。全楼采用框架结构,基础形式采用独立柱基,基础埋深2.74 m,基础宽度与长度均为3.2 m,基础覆土容重为20.0 kN/m3,基底压力平均值180.0 kPa,基底压力最大值是216.0 kPa,地下水埋深为4.05 m。采用CFG桩复合地基处理,三角形布桩,桩径0.5 m,桩竖向间距1.1 m,桩水平间距1.1 m。总桩数184根。
4 计算工程实例的沉降
鉴于本工程选择的3个静载荷试验检测点与计算点并不重合,而为了能更好地对理论计算结果的准确性进行判断,从中选择1个与检测点相近的计算点为例进行计算验证。其中2号计算点(71号钻孔,D轴/1轴,J-12基础)与7#检测点相近,并在同一基础内(图2),相对而言具有较好的对比性。
沉降变形计算深度:
zn= 3.0+6.0+2.7-2.74=8.96 m
(见图3中的71号钻孔)。
沉降计算深度验算:
由于基础宽b=3.2 m,Δz=0.6 m,

4.1 规范法计算
2号点的基础底面处附加应力值:
p0=pk-γD=180.0-17.0×2.74=133.42 kPa
(8)
各土层的沉降示意见图4,压缩量计算结果见表4。

图4 规范法沉降示意图Fig.4 Schematic diagram of normal settlement

表4 各土层沉降计算Table 4 Settlement calculation of each soil layer

(9)
(10)
通过查表1可知沉降计算经验系数ψs取值为0.622。
总沉降量:
1.23+7.22)=27.88 mm
(11)
4.2 双层应力法计算
2号点的基础底面处附加应力值:
p0=pk-γD=180.0-17.0×2.74=133.42 kPa,沉降变形计算深度为Zn=8.96 m。
计算桩间土顶面和下卧层顶面处应力水平系数δsr、δss:
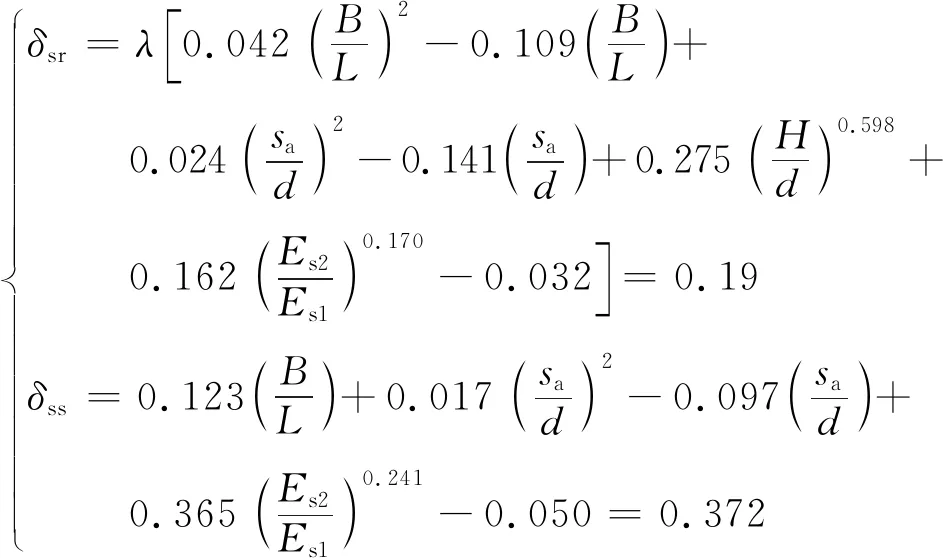
(12)
计算桩间土顶面和下卧层顶面处附加应力值psr、pss:
(13)
查表1知沉降计算经验系数为ψ1=0.58,ψ2=0.971,最终沉降变形量为
(14)
4.3 基于规范修正的公式计算
2号点的基础底面处附加应力值:
p0=pk-γD=180.0-17.0×2.74=133.42 kPa,沉降变形计算深度为Zn=8.96 m。
通过查表1可知沉降计算经验系数为ψ1=0.58,ψ2=0.971 。
下卧层顶面附加应力值:
(15)
最终沉降量为
s=ψ1s1+ψ2s2
(16)
4.4 静载荷试验结果分析
CFG桩复合地基静载荷试验p-s曲线图,见图5和图6。

图5 7#CFG桩复合地基p-s曲线Fig.5 p-s curve of 7#CFG pile composite foundation

图6 7#CFG桩复合地基s-lgt曲线Fig.6 The s-lgt curve of 7#CFG pile composite foundation
检测点在最大加压荷载作用下,复合地基承压板最终沉降量是23.18 mm;卸载至0时,残余沉降量为13.95 mm。静载荷试验曲线属缓变型。
4.5 沉降观测结果分析
32栋楼共布设了8个沉降观测点,分别为L1~L8(图2),最大累积沉降量为10.36 mm(L6号测点),最小累积沉降量为4.67 mm(L1号测点);平均沉降量为7.24 mm,相邻点间最大沉降差为3.2 mm;最大沉降量的沉降速率为0.12 mm/d。
沉降观测成果见图7,所测建筑物的沉降变化均符合一般规律。

图7 沉降观测成果曲线Fig.7 Curve of settlement observation result
5 沉降计算与静载荷试验结果、沉降观测结果对比
三种方法的计算结果与静载荷试验结果、沉降观测结果见表5。
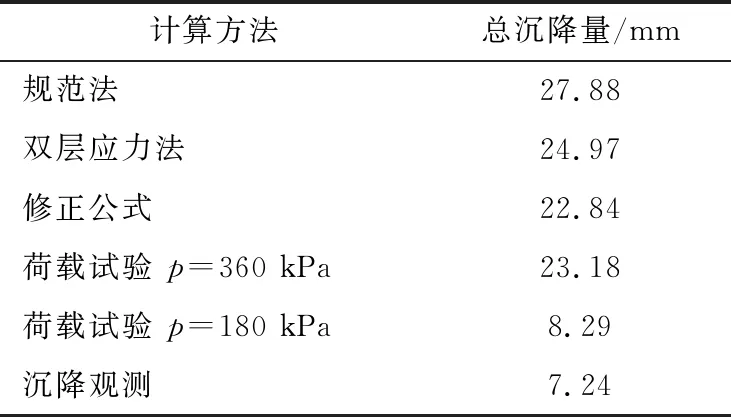
表5 沉降计算与静载荷试验结果、实测沉降对比Table 5 Settlement calculation and static load test result and measured settlement comparison
本文以2号计算点为例,通过计算得知几种方法计算最终沉降量分别为27.88 mm、24.97 mm、22.84 mm。本工程共选取了3个点位进行复合地基载荷试验,其中2号计算点与7#检测点位置较近,并位于同一基础内,相对来说有可比性,可以作为本文沉降变形计算的对比验证。7#静载荷试验检测点沉降量为23.18 mm,对比三种计算方法都与试验实测值有一定的偏差。静载荷试验的最终静载压力是房屋建成后压力的1倍,若当荷载p=180 kPa时,7#静载荷试验检测点沉降量为8.29 mm,与实测沉降平均值7.24 mm比较相近,结果可靠。在这三种计算方法中以规范法偏差是最大,双层应力法偏差较小,而修正公式计算结果略小于试验值。从理论上分析,三种计算方法计算的下卧层沉降量应该相同,都是采用分层总和法,但由于桩端处附加应力取值不同,造成下卧层沉降量存在偏差。
1)双层应力法在误差上较小,十分接近实测值,但该方法是由试验拟合而来,难以保证其稳定性、适应性,且该方法存在着计算量繁琐的缺陷,在工程中并不适用。
2)修正公式误差相比规范法要小,虽出现略小于试验值的情况,分析可能是计算下卧层顶面处附加应力所取的压力扩散角的误差所导致,但此方法在计算上浅显易懂,源于规范法的思路,同时也结合了双层应力法的优点,计算下卧层沉降量较为合理,计算结果更加优于规范法,相比之下,规范法就显得较保守了。
通过几种计算方法的对比分析,在具体工程中,采用修正公式虽存在一定的误差,但这种误差在可接受的范围内,因此,可将此公式运用于类似工程对地基沉降变形进行预测。
6 结语
结合桂林当地实际工程案例对沉降变形计算进行分析,修正公式计算结果相对规范法更加优越,同时验证了修正公式的可行性,可用于工程实践中。通过对比可知任何一种计算都有其局限性和误差性,所以应根据工程实际情况,合理选择计算方法,同时要结合工程实践中形成的经验,加以分析和对比,从而使计算结果更加合理、准确,既要保障安全性,也要考虑经济性。
