基于改进蝙蝠算法的电力系统节能发电调度策略研究

程 琳，陈 财，刘 影，于 传，胡 炜

( 1.安徽电气工程职业技术学院，安徽合肥 230051；2.国网安徽省电力有限公司培训中心，安徽合肥 230022； 3.电子科技大学，四川成都 611731)

0 引言

能源是社会经济发展的动力源泉，随着全球自然资源消耗不断加剧，能源供给短缺问题日益严重，如何保障生态环境、促进能源合理利用成为社会各界广泛关注的焦点[1].随着水电发电规模不断扩大，电力工业面临着水电、火电并网、协同优化的问题.文献[2]采用数学分析方法对水电与火电联合运行经济性问题进行了分析.文献[3]研究了水火电最优协调方程，在电力行业得到广泛应用.针对如何有效提高电力系统运行经济性、安全性和环保性等问题，文献[4-7]采用了不同的目前热门的人工智能算法探讨了电力系统调度优化问题.文献[8]描述发电机出力与成本之间的关系，采用分段函数和非线性函数来计算成本，并通过阀点效应来构建电能生产成本模型，但由于采用了非连续性的跳跃性函数作为分析工具，这会大大提高模型求解难度.文献[9]将电网的优化目标从对投入运行的成本最小化向用户的购电成本最小化转变.从而在市场化环境下，将电力企业最优化目标体现为市场经济性需求.文献[10]将火电企业将实时费用最小、水火置换效率最高等作为优化调度目标，但文献中没有综合考虑所有影响水电发电企业经营效益的因素，如忽视了经济性、环保性等问题.

通过分析近年来相关研究文献可以看出，优化准则并非是固定不变的，而是要在水火发电机内在规律和机制基础上，根据电力行业政策、环境保护、市场体制等因素的变化，以制定更加科学合理的电力系统运行目标.因此，本文首先研究了负荷与电网中发电厂之间的特性关系，通过重点研究水电站运行特性、火电站运行特性以及水火电电力系统间的协调运行特性，从而构建了考虑负荷变换的水、火电站的电力系统优化问题数学模型，并采用改进的蝙蝠优化算法对模型进行优化处理.

1 考虑负荷变换的水、火电站的系统特性分析

在大电网运行的某个时间周期内，大电网中的水、火电站会按照负荷分布特性各自承担部分变换的负荷量.设：水电站承担的负荷量为PDh，火电站承担的负荷量为PDTh.大电网系统中总负荷量可以由水、火电站的负荷承担，因此特性方程可以采用式(1)予以描述：

(1)

式(1)中PD为电网总的负荷，at,bt,ct为随时间变化的系数，通常取值范围为0～1，PTh表示火电站出力，由于希望火电站承担负荷量最优.因此，式(1)中火电站机组对不可再生的燃煤料所消耗量最小的目标函数可以表示为：

(2)

其中λ为调节变量，式(2)的最优条件为：

(3)

通过式(3)求解可以得到火电机组在燃煤料消耗量最小时所对应的机组最大出力：

(4)

通过最优条件式(2)求解后，由式(4)可知，在调度周期内，火电机组在各个时段承担的负荷是均匀的，并且处于基本相等的状态.在这种求解条件下，火电机组对燃煤料的消耗量才能够达到最小值.因此在工程实际应用中，我们可以在大电网的节能调度中将水电厂承担多余的变化负荷而火电厂承担电网中基本负荷量.

2 水、火电站的节能发电调度目标优化

为了进一步实现水、火电站间的节能发电调度的目标优化，我们在式(1)的数学模型的基础上，分别引入了大电网的网络损耗最小以及水电站用水量最佳等目标函数，并将它们与火电站的煤耗量最小化一同作为新的目标函数，共同构成大电网系统考虑水、火电站间协调配合的节能发电调度目标函数.

2.1 电网网络损耗最小化目标函数

大电网中的网络损耗越小，预示着电力系统在运行时实现的经济性越高.目前，对于电网建立网络损耗数学模型普遍是基于潮流方程，对每个节点的节点电压分别进行建模，所建模型为式(5)所示.

(5)

式(5)中，K表示大电网中的节点数目；Vi、Vj、θi、θj以及Rij、Xij分别表示电网中节点i、节点j的电压、相角以及节点i与节点j之间的电阻值、电抗值.通常，式(5)也可以采用式(6)的简化模型进行表示.

(6)

式(6)中，Pgi、Pgj分别表示电网中节点i与节点j的注入有功功率.BiQ、Bij、BQQ为电网的网络损耗计算系数.那么，可以得到电网网络损耗最小化目标函数为：

(7)

2.2 水电站用水优化目标函数

我们根据水电站的运行特性以及水电站的弃水策略，提出通过调节水电站蓄水量，使其最大化，从而实现水电站动态弃水的目标函数，如式(8)所示.

(8)

式(8)中，NL、Vendi分别表示具有调节功能的水电站个数，以及第i个水电站的蓄水量，而每个水电站的蓄水量是根据负荷量变换情况进行动态调节.

综上我们可以得到考虑负荷变换时，含水、火电站的电力系统节能发电调度多目标优化的目标函数：

(9)

式(9)的约束条件为：

(1)电力系统的负荷平衡约束条件：

(10)

(2)火电站的运行约束条件

(11)

(3)水电站的运行约束条件：

(12)

式(9)～式(12)就构成考虑负荷变换时，含水、火电站的电力系统节能发电调度的多目标优化数学模型.

3 蝙蝠算法及其改进

3.1 蝙蝠算法基本原理

fi=fmin+(fmax-fmin)β

(13)

(14)

(15)

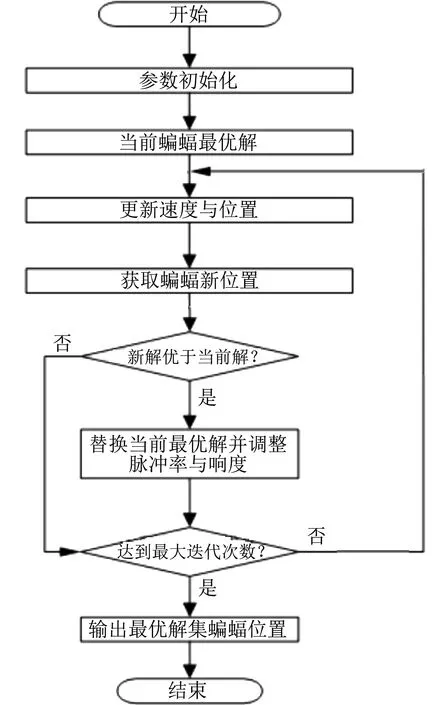
图1 蝙蝠算法的基本原理流程框图Fig.1 Principle flow chart of bat algorithm

3.2 蝙蝠算法的改进

通过分析蝙蝠算法使用的主要策略，发现在算法中，式(16)提供局部搜索从而获得最优解.但是，不难看出，式(16)的局部搜索能力不是很强，因此为了提高算法的收敛速度，我们需要平衡蝙蝠的局部搜索能力和全局搜索能力.

飞行距离在蝙蝠算法中就是步长.在算法中，飞行距离每完成一次调整，就会产生一个最优值，记为xold.那么，在下一次迭代中，xold被作为当前的优化解，参与调整，通过调整后又会获得一个新的最优解xnew，蝙蝠算法的迭代过程满足式(16).

xnew(i)=xold+εAt

(16)

式(16)中，ε为满足[-1,1]均匀分布区间中的一个随机数；At表示响度平均值.因此，参数间的调整满足如下定义式：

At+1(i)=αAt(i)

(17)

式(17)中，α∈(0,1)，是一个随机数.我们对解向量及其目标函数值重新以矩阵形式进行表示：

(18)

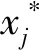
(19)

chi+1=chi×(1-chi)(0≤i≤K)

(20)

K是混沌序列的长度，chi∈(0,1)是一个随机数.然后将chi映射到间隔时间[xl,xu]内的混沌矢量CHi中.

CHi=xl+chi×(xu-xl)

(21)

(22)

λ是收缩因子，它的定义如下：

(23)

由式(23)可以看出，λ会随着进化代数的增加而减小，即随着进化的进程，局部搜索范围会变小.改进蝙蝠算法在前面构建的含水、火发电站的发电调度多目标优化模型中应遵循如下的步骤：

(1)系统参数初始化，主要包括水、火电电力系统各节点电压等基本参数以及改进蝙蝠算法初始参数.

(2)根据式(18)～式(23)，更新速度与位置.

(3)定义一个满足[0,1]均匀分布的随机数rand，判断rand是否满足约束条件.如果满足，转到(4)；反之，根据式(16)进行局部搜索，直到满足约束条件，进入步骤(4).

(4)获取位置新解.

(5)判断位置新解是否优于原来的最优解，并判断rand是否满足rand

(6)更新位置参数.

(7)判断位置新解是否优于当前解.如果满足，转到(8)；反之，转到(9).

(8)以位置新解代替当前最优解，再次更新位置、速度.

(9)判断是否达到最大迭代次数.如果满足，转到(10)；反之，回到(2).

(10)输出蝙蝠算法最优解，算法结束.

4 实验仿真

仿真选用了8座水电站、10座火电站以及500kV电网进行案例分析，这8座水电站一次记为：AB、BC、CD、DE、EF、FG、GH、HI.这10座火电站依次记为：JK、KL、LM、MN、NO、OP、PQ、QR、RS、ST.根据电网的实际运行数据，得到大电网系统的一天内日负荷数据，见表1.8座水电站的水能指标参数及水库特征参数分别如表2所示.10座火电站采用数值拟合后得到的参数见表3.

表1 电网日负荷数据Tab.1 Daily load data of power grid

表2 8座水电站水能指标参数Tab.2 Index Parameters for eight Hydropower Stations

表3 10座火电站参数Tab.3 Parameters of ten thermal power station

改进蝙蝠算法参数初始值定义如下：fmax=1；fmin=-1；At=0.25；α=0.95；n=50；maxcycle=1000.

选取水电厂动态弃水策略下蓄水量最大化、火电厂综合耗煤消耗量最小化作为相应的目标函数，应用改进蝙蝠算法进行多目标优化，其结果如图2所示.

图2 多目标优化结果Fig.2 Multi-objective optimization results

由图2可知，基于改进蝙蝠算法的水火电节能发电调度多目标优化共计获得33个非支配的解，在图2中表示为相应的点.图2中纵坐标日能源消耗量表示应最大程度使用的水电厂发电，横坐标污染物排放量表示在源消耗量中火电厂综合耗煤消耗量应最小.最优解对应的蓄水量是1 345 850.72 t，综合燃料消耗量为295.11 t/d.本文选用蝙蝠算法与改进蝙蝠算法做比较，其结果如表4所示.

由表4可以看出基于改进蝙蝠算法的含水、火电站的电力系统节能发电调度要比采用传动蝙蝠算法更能节约蓄水量和燃料的消耗量.

5 小结

本文在考虑负荷特性基础上，结合火电站的煤耗量最小化目标，大电网的网络损耗最小以及有对水电站蓄水量的调节最大化等多目标的优化目标函数，从而整体构建了含水、火电站的电力系统节能发电调度多目标优化数学模型.在模型求解中，本文采用同时实现局部最优与全局最优的蝙蝠算法，并在分析蝙蝠算法基本原理和工作过程的基础上，引入参数动态更新与混沌因子，形成了改进蝙蝠算法.仿真结果表明，采用改进蝙蝠算法能够对所建的多目标模型进行优化处理，得到节能发电调度结果比采用传统蝙蝠算法更能够满足设置的约束条件.