函数值域的求法
2020-03-02陆丰市第二职业技术学校
文/陆丰市第二职业技术学校
求函数值域是中学数学的一个重要内容,它贯穿于整个中学数学的始终,也是与实际应用衔接最紧密的内容之一。本文对如何求值域作了系统介绍,对某一类题,用什么方法较为简捷,并用适当的例子加以说明,而且还对每一种方法的概念、适合类型、注意事项等作了全面的概括。
一、观察法
根据函数值域的定义,函数值域可由定义域及对应法则确定,因而对某些简单的函数,可在定义域及对应法则基础上通过观察确定函数值域。
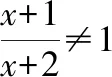
故值域为:y∈(-,1)∪(1,+)
在求这种有理分函数的值域时往往出现两方面错误:一是既然定义域要除去使分母为零的值,值域也一定要除去某些值;另一是不考虑分式的特征而认为值域一定为一切实数。这两方面的错误都应注意避免。
二、利用基本函数的性质
通过对解析式的分式、变形,然后借助于基本函数的值域逐步推求原函数的值域。
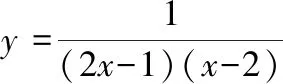


所以,y的值域为:(-,)
三、反函数法
当函数存在反函数又不难求得时,可以把求原函数的值域转化为求反函数的定义域。

它的定义域为x∈(-1,1)
所以原函数的值域为y∈(-1,1)

四、配方法
根据式于a2≥0,可以对含有二次三项式的函数进行配方,化成平方式的形式,然后根据定义域求值域。
解:∵-x2+2x+3=-(x-1)2+4≤4
又∵在函数的定义域上,显然y≥0
所以原函数的值域为:y∈[0,2]
五、判别式法
当函数不存在反函数或反函数存在但不易求得时,有时可将原函数转化成一个常数项中含y的关于x的二次方程,利用判别式来求函数的值域,这个方法可用于无理函数的值域的求解当中。
解:原式移项,两边平方整理得:
8x2-16yx+(3-16y2)=0
∵为实数
∴Δ=(-16y)2-4×8×(3-16y2)≥0


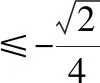

六、替换法

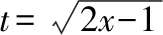
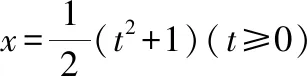

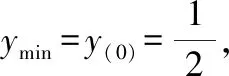

替换法除了上述的代数换元法,还有三角换元法。
七、不等式法
利用基本不等式、柯西不等式等来求函数值域。
解:∵x>3
∴x-3>0
=5
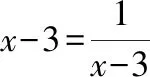
所以函数的值域为y∈[5,+)
用基本不等式求值域,应注意不等式的适用范围及等号成立的条件。
八、函数单调性法
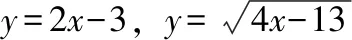
九、用方程的观点求函数的值域
下面先给出一个定理:
定理:已知函数y=f(x)(x∈A)的值域为C且关于x的方程f(x)-y=0在A中至少有一解的y的集合为D,那么C=D。
解:原式等价于:
x2-xy+1=0(x>0)
设g(x)=x2-xy+1,由g(0)=1,
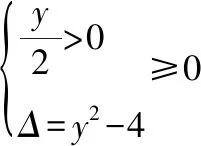
函数g(x)的图像与x轴正半轴相交,所以方程x2-xy+1=0在(0,+∞)内有解的条件为y∈[2+)由定理可知函数的值域为y∈[2+)。
十、导数法
很多较复杂的函数的最值可以利用导数求得,这也是寻求某些函数值域的行之有效的方法。这种方法首先求出函数的导数,然后解出导数值为0的驻点,再判别函数的单调性,最后求出值域。
十一、最值法
最大值最小值定理:若函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值与最小值。设函数f(x)在定义域[a,b]上的最大、最小值分别是M和m,则f(x)的值域为[m,M]。
十二、极限法
有些函数可运用极限的知识来求值域。
十三、图像法
有些函数可以根据其函数图像求出其值域。
求解函数值域的方法很多,其实各方法之间是相互联系的,一道题可能有多种解法,至于用什么方法好,还需要学生在实践中不断总结。
