6-UPS并联机器人运动反解误差建模及补偿

李帅， 张学科

（广西科技师范学院职业技术教育学院，广西来宾545004）

关键字：矩阵变换法；运动反解；并联机器人；最小二乘法

0 引 言

6-UPS并联机器人是由上平台、6个上铰链、6个驱动杆、6个下铰链、下平台5部分组成，如图1所示。因为6-UPS并联机器人具有整体刚度好、系统响应快、承载能力大等特点，所以是一种理想型大负载、高频响空间运动模拟器[1]。常用来测试大型装备综合性能，如模拟飞行器在强对流天气中飞行、舰船在条件恶劣的海面上航行、战车在地形复杂的山地作战等情况。6-UPS虽然运动精度高，但在运动过程中不可避免地会存在着运动误差，导致机器人运动终端不能达到预定的位置，降低了位置精度。然而位置精度是检验6-UPS并联机器人性能的一项重要因素，他直接决定测试装备运动性能的优劣。为了减小并联机器人运动误差，提高运行精度，优化6-UPS并联机器人的运动误差是很有意义的。

图1 6-UPS并联机器人

1 6-UPS并联机器人误差来源

6-UPS并联机器人误差主要分为静误差和动误差。静误差是指与工艺系统初始状态有关的原始误差[2]，6-UPS并联机器人静误差主要来源于上铰链定位误差、下铰链定位误差、驱动杆件长度误差；上铰链定位误差、下铰链定位误差、驱动杆件长度误差均来源于加工误差、安装误差和测量误差。而动误差是指研究对象在运动过程中由于摩擦力、热力等因素作用，使研究对象产生受力变形、受热变形、磨损、内应力变化[3]，从而影响研究对象在调整中获得的相对位置精度。6-UPS并联机器人动误差主要来源于伺服控制系统误差、驱动杆伸缩误差。伺服控制系统误差来源于伺服系统的稳态误差和静态误差[4]，驱动杆的伸缩误差取决于杆件的弯曲稳定性[5]。由于产生动误差的因素过于复杂，所以分析优化静误差是本文的研究重点。

2 6-UPS并联机器人反解误差建模

图2 平台位置描述

在6-UPS并联机器人初始状态下，上、下平台坐标系o-xyz，O-XYZ分别处在各自的圆心上，如图1所示。当上平台运动时，坐标系oxyz的新位置可以视为下平台坐标系O-XYZ通过旋转与上平台坐标系oxyz相同的角度之后，再平移Oo 长度获得的坐标，如图2所示。因此，上下平台存在着一定的位置关系。即设上下平台各铰点ai，Ai（i=1,2…6），则驱动杆件空间长度矢量表达式为

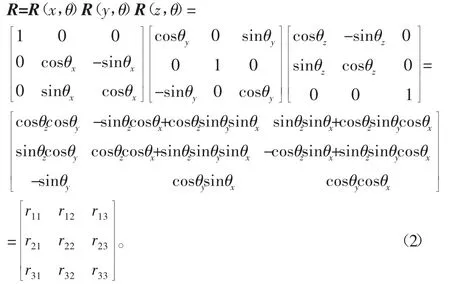
代入式（1）得：

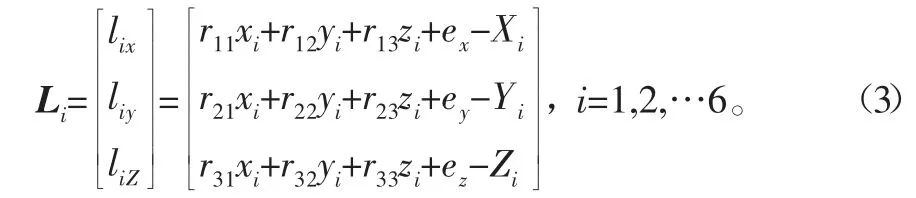
根据式（3），驱动杆长为

当上平台处于初始状态时，即R=R（x，0）R（y，0）R（z，0），E=0，则驱动杆件初始空间长度矢量L0就可以确定为

由于上下平台各铰点安装时会出现一定位置误差，如图3所示。所以导致各铰点坐标值发生微量变化，致使各驱动杆件位移量也因此发生变化。此时，各驱动杆件空间长度矢量表达式为

式中：ai′（xi′,yi′,zi′），Ai′（Xi′,Yi′,Zi′），i=1,2, …6为上下平台由于安装误差而得到的铰点位置。根据式（1）～式（3），各驱动杆件误差矢量ΔLi，i=1,2,…6，表达式为

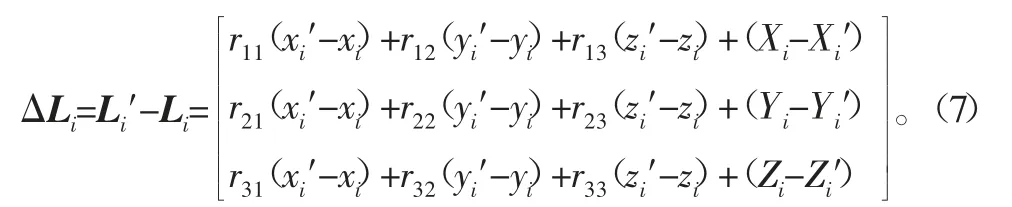
根据式（7），各驱动杆件误差Δli为

式（8）为6-UPS并联机器人根据运动学反解而建立的驱动杆件位移误差模型。

3 6-UPS并联机器人运动误差补偿

最小二乘法原理是一种数学优化方法，可以使求得的数据与实际数据之间误差的平方和为最小。由于安装误差的存在，6-UPS并联机器人铰点在安装过程中会出现位置安装误差，如图3所示。这些安装点分布在理想安装点的周围，所以让实际安装铰点尽可能地靠近理想安装点，进而达到对平台安装位置误差进行补偿的目的。利用最小二乘法原理拟合球面的方法对上下平台各铰点安装误差进行拟合，使实际安装点尽可能靠近理想安装点，减小安装误差。

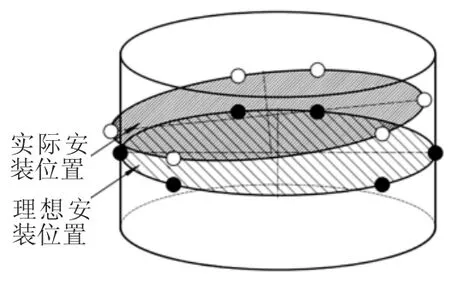
图3 铰点安装位置

以下平台为研究对象，各铰点坐标为Ai（xi，yi，zi），i=1,2,…6，实际各铰点的安装位置均分布在理想安装位置的周围，依据球面方程:

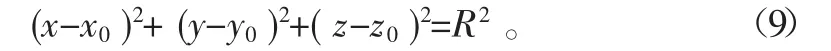
令函数M0(x0，y0，z0，R)为目标优化函数，找出函数M0最小值为

根据式（11），补偿后驱动杆件误差矢量ΔLi（i=1,2,…6）为

根据式（12），补偿后驱动杆件误差为

同理，上平台也用相同的优化方法，优化结果如图5所示。以研究对象为例，上平台绕着X轴转动10°，此时，各驱动杆件根据式（1）～式（8）计算出各铰点位置补偿前的位移误差，根据式（9）～式（13）计算出各铰点位置补偿后的位移误差，计算结果如表1所示。从表1可以看出，驱动杆件在补偿之后的位移误差要小于补偿之前的位移误差值，说明利用最小二乘法原理，对平台各铰点进行球面拟合的优化办法来补偿平台安装误差是合理可行的。

图4 对下平台各铰点优化结果

图5 对上平台各铰点优化结果

表1 位移误差

4 结 语

本文首先分析了6-UPS并联机器人误差的来源，明确了误差优化方向。其次利用运动学反解对驱动杆件位移误差进行建模，为误差优化提供理论基础。然后通过对存在安装误差的平台各铰点进行分析，建立了目标函数并对目标函数进行优化。最后通过分析实例进行结果比对，证明了使用球面拟合的优化办法对平台各铰点安装误差进行拟合优化是合理可行的。