基于MATLAB软件的机电悬挂连杆机构的运动学分析
2020-03-02段国柱宋慧新陈宇侯友山中国北方车辆研究所北京100072
段国柱,宋慧新,陈宇,侯友山(中国北方车辆研究所,北京100072)
0 引 言
机电悬挂是一种新型车辆用悬挂,是集机、电、控制于一体的悬挂形式。相对于传统悬挂,其能实现主动控制、半主动控制,同时能实现振动能量的回收并实施有效管理。机电悬挂实现被动控制或者半主动控制时,其工作原理是将地面给予负重轮的振动通过一套四连杆机构传至摇臂,通过机电悬挂中的增速机构,带动电动机转子高速旋转,使电动机发电,同时将电能以热能的形式耗散掉或者储存起来。主动控制时,指令控制电动机运转,通过减速增扭机构,驱动摇臂旋转,再通过四连杆机构带动平衡肘上下运动,以减轻地面对负重轮的冲击。可以看出无论发电过程还是主动控制过程,四连杆机构都是其中重要的传动机构,对四连杆机构进行运动学分析,确定输入运动与输出运动的关系尤其重要。文中利用计算能力、数据分析处理能力强大的MATLAB软件[1-2]对机构的运动特性进行分析,清晰地给出了摇臂摆角、角速度与平衡肘摆角之间的关系曲线图,同时给出了任意时刻四连杆机构的杠杆比曲线。
1 建立数学模型
该机电悬挂实物图如图1所示,其结构简图如图2所示,机电悬挂连杆机构运动学分析图如图3所示。

图1 机电悬挂实物图

图2 机电悬挂结构简图
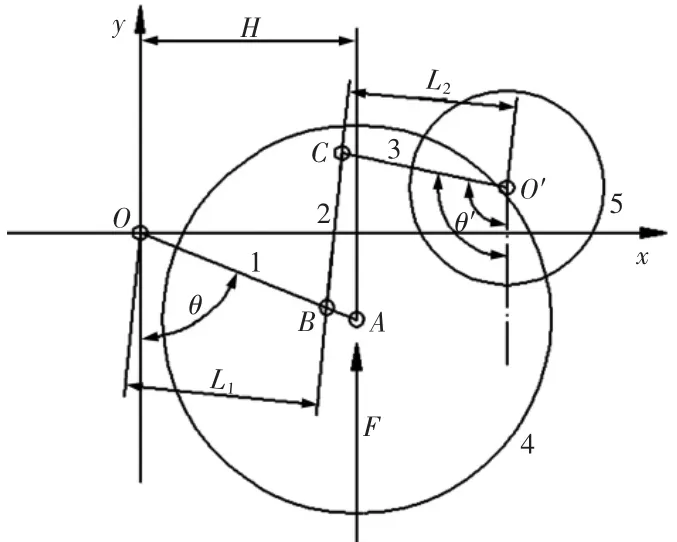
图3 连杆机构运动学分析图
在图3中,构件1表示平衡肘,构件2表示连杆,构件3表示摇臂,构件4表示负重轮,构件5表示机电执行器。O为平衡肘的旋转中心,O′为摇臂(机电执行器)的旋转中心。车辆行驶时,负重轮在地面上下跳动,带动平衡肘上下摆动,通过连杆驱动摇臂摆动。假定平衡肘与竖直线的夹角为θ,摇臂与竖直线的夹角为θ′,线段OA的长度为r1,线段OB的长度为r′,线段BC的长度为l,线段O′C的长度为r2。
1.1 摇臂角位移分析
下面通过解析法[3]分析平衡肘摆角和摇臂摆角之间的关系式。图2中O点的坐标为(0,0),O′点的坐标为(a,b)(a,b均为正数),A点的坐标为(r1sinθ,-r1cosθ),B点的坐标为(r′sinθ,-r′cosθ),推算出C点的坐标为(a-r2sinθ′,br2cosθ′),由此推算出线段BC的长度计算公式为:

上式即为平衡肘摆角和摇臂摆角之间的关系式。
1.2 摇臂角速度分析
在这里我们将θ看成是平衡肘摆角对时间的关系式:θ=f(t);将θ′看成是摇臂摆角对时间的关系式:θ′=φ(t);在公式(1)的两边同时对时间t求导,得出平衡肘角速度和摇臂角速度的关系式:

对于我们分析的机电悬挂装置而言,当平衡肘位于初始位置时,平衡肘与竖直线的夹角θ=53°。
1.3 运动机构的杠杆比分析计算
机电悬挂可以实现半主动控制和主动控制。当其作为被动悬挂使用时,执行器实质是一个减震器;当其作为主动悬挂使用时,它就是一个作动器,可以主动输出控制力矩。
当执行器作为减震器使用时,假定其产生的阻力矩为MR,那么将阻力矩转化为负重轮上的力为FR=MRL1/(L2H);当执行器作为作动器使用时,假定其输出主动力矩为MZ,那么将主动力矩转化为负重轮上的力为FZ=MZL1/(L2H)。
在这里我们把L1/L2定义为该机构的杠杆比,将其用i表示。下面通过解析法计算i的值:
BC线段的斜率为
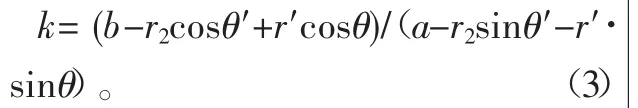
BC线段的方程为

将BC线段上B点的坐标代入方程得:

BC线段的方程可以描述为:

O点到BC的距离为
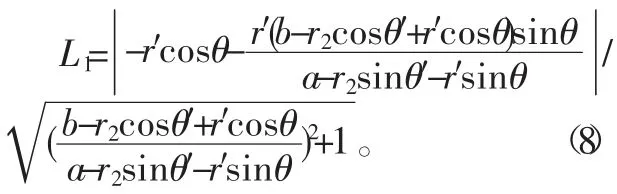
O′点到BC的距离为:

2 计算实例
在现有的机电悬挂装置中, 已知:r1=360 mm;r2=260 mm;r′=310 mm;l=240 mm;a=566 mm;b=70 mm。
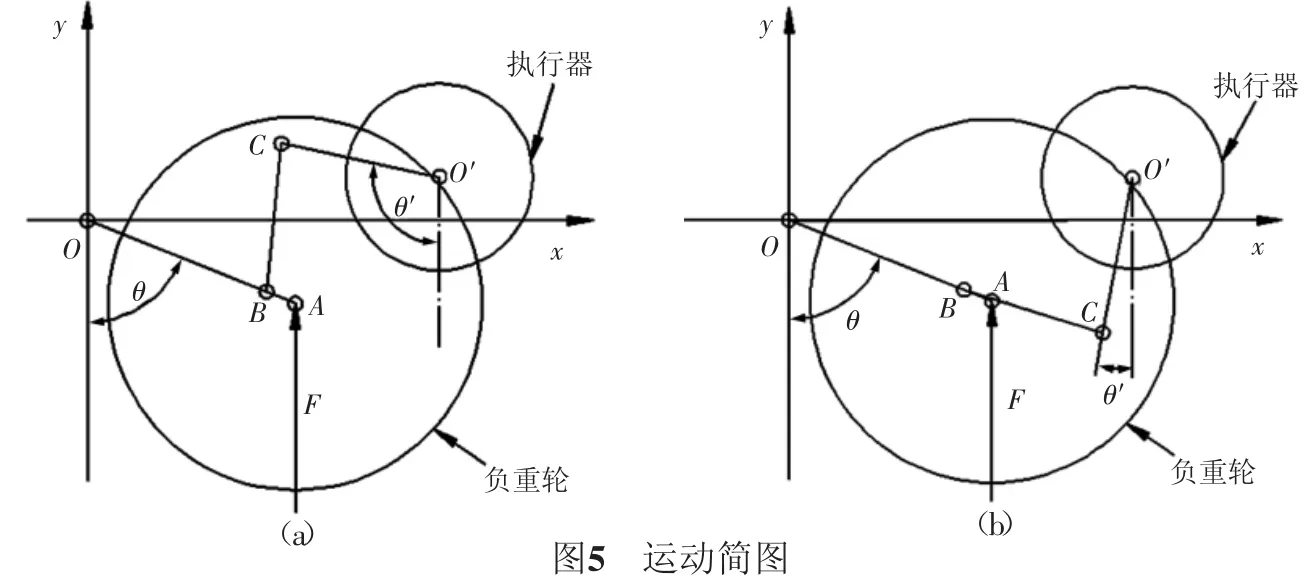
1)运用MATLAB软件可以得出θ和θ′的关系曲线,如图4所示。从图形可以看出,每一个θ对应两个θ′值,这是因为在机构运动中,每一个平衡肘的位置有两个摇臂位置与之对应,如图5所示。
我们考虑的是图5(a)中所示运动状态,从图形可以看出当平衡肘处于平衡位置时,平衡肘与竖直线的夹角θ=74.43°,通过计算分析得出θ′ =109.26°。

图4 摇臂摆角与平衡肘摆角的关系曲线
2)通过 运 用MATLAB软件可以得出摇臂角速度和θ的关系曲线(假定平衡肘的转动角速度为10 r/min),如图6所示。
3)通过运用MATLAB软件可以得出该悬挂装置的杠杆比平方与θ的关系曲线,如图7所示。

3 结 论
通过建立机电悬挂连杆机构的数学模型,并运用MATLAB软件的强大的计算、数据分析处理能力对该机构的运动进行编程求解,得出了该机构的重要运动参数,这一方法简单、便捷,为机电悬挂连杆机构的设计提供了重要的依据。
