四川长宁6.0级地震库仑应力变化及其对余震的触发作用

章 阳 ,陈 婷 ,王利兵 ,罗 娜 ,张朋杰

（1.河北省地震局石家庄中心台,石家庄 050021;2.河北省地震局预测研究中心,石家庄 050021;3.河北省地震局红山基准台,河北 邢台 054000）

0 引言

中国地震台网中心正式测定,2019年6月17日22时55分在四川宜宾市长宁县（28.34°N,104.90°E）发生6.0级地震,震源深度8 km,震源机制解为逆冲兼走滑型地震[1]。本次地震序列较为活跃,截至8月20日,共记录到3级以上余震64次,其中3.0～3.9级地震52次,4.0～4.9级地震8次,5.0～5.9级地震4次,分别为6月17日23时36分5.1级地震,6月18日7时34分5.3级地震,6月22日22时29分5.4级地震,7月4日10时17分5.6级地震。1900年以来,震中50 km内未发生6级以上地震;震中100 km内发生过2次6级以上地震,震中100～200 km内发生6.0～6.9级地震5次,这些6级以上地震均发生在川滇块体东边界的马边—大关地震带。此次地震位于川东南地区北东向华蓥山断裂的东南方向,发生在四川盆地边缘的长宁背斜构造附近规模不大的次级断层上,根据主震和余震分布方向,推测发震断层为长宁—双河大背斜[1],这与上述6级以上地震以及发生在龙门山断裂带的汶川8.0级地震和芦山7.0级地震处于不同的构造位置。由于本次地震余震比较丰富,对于余震的危险性评估很有必要,因此,本文综合考虑同震位错和震后粘滞松弛效应,采用粘弹性模型计算主震的库仑应力变化,分析主震对余震的触发作用,根据长时间尺度库仑应力动态变化特征为预测后续余震提供地点依据。长宁地震区域地质构造如图1。

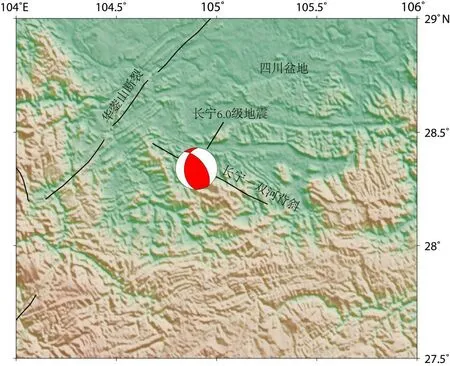
图1 长宁地震区域地质构造图Fig.1 Geological structure of Changning earthquake region

静态库仑应力变化被应用在分析大地震对余震分布的影响中,研究认为静态库仑应力改变量超过0.01MPa（0.1bar）可以影响余震的发生位置[2]。库仑应力增强触发后续地震,反之则推迟后续地震发生[3],因此,库仑应力在余震危险性评估和地震中长期预报中应用广泛。国内众多学者开展利用库仑应力动态演化分析断裂带上地震活动时空变化过程,进一步分析区域地震危险性。万永革等[4]计算1900年以来青藏高原东北部发生的7级以上地震库仑应力积累和演化的过程,并且讨论大地震发生之间的影响,发现库仑应力对大震的触发率达85%;邵志刚等[5]计算汶川8.0级地震引起的库仑应力动态演化,结合地震学和地质学资料分析活动断裂危险性,并指出在分析强震库仑应力时不能忽略震后效应;徐晶等[6]研究川滇菱形块体东边界断裂带内库仑应力演化及危险性,认为强震之间可能存在触发作用,并根据库仑应力的显著增加,给出断裂带上的强震危险性区;靳志同等[7]根据前续断层在后续断层的库仑应力变化给出汶川地震的破裂传播方向;靳志同等[8]基于均匀弹性半空间模型分析九寨沟7.0地震的同震库仑应力变化对余震的触发;

然而,基于弹性变形的模拟[9]只能估计应力变化的弹性响应,能模拟地震后较短时间内的应力应变场变化特征。但对于较长的时间间隔（数十年）,便不能忽略粘弹性松弛效应。在地震应力转移的应力触发研究及地震危险性估计过程中,考虑粘弹性应力松弛十分重要。程佳等[10]利用粘弹性地壳模型计算历史地震对九寨沟地震的同震和震后库仑应力作用,认为历史强震促进九寨沟地震的发生,并计算九寨沟地震对周边断层的地震危险性影响;尹凤玲等[11]基于分层半无限空间粘弹性模型,计算红河断裂带上25次强震由于同震应力阶变、震后粘滞松弛和震间构造应力加载综合作用的库仑应力变化的演化过程,进而分析地震危险区;刘琦等[12]基于位错理论和粘弹本构关系,分析汶川地震和芦山地震的同震位错和震后粘弹松弛效应对周边区域的地壳形变场、应力场、断层活动状态及地震危险性等的影响;黄禄渊等[13]综合考虑同震静态应力和震后粘弹性应力分析汶川地震对九寨沟地震的影响。Pollitz等[14]认为,用Burgers体模型能更好模拟震后的粘滞松弛效应,计算震后库仑应力变化。Wang等[15]编写粘弹性应力应变程序PSGRN/PSCMP程序,该程序基于Burgers粘弹性模型[16],考虑地球重力对形变场的影响,可计算同震和震后长时间尺度的应力变化。

因此,本文综合考虑同震位错和震后粘滞松弛效应,基于Burgers粘弹性模型,利用PSGRN/PSCMP程序计算地震破裂面上产生的库仑破裂应力变化,分析主震对3级以上余震的触发作用,进而为后续的余震预测提供地点依据。同时,计算粘弹性模型的长时间尺度库仑应力动态变化,根据粘弹性模型的震后长时间尺度库仑应力动态演化特征进一步分析区域地震危险性。

1 库仑应力变化

根据库仑破裂准则,当岩石发生破裂时,破裂面上的库仑应力（CFS）可定义为

式（1）中,τ为破裂面上的剪应力;μ为内摩擦系数;σn为正应力,张开为正,压缩为负;p为地壳内部的孔隙产生的张性应力,S为剪切强度。当剪应力τ 越接近于S-μ(σn+p),库仑破裂应力CFS越接近0,材料越容易破裂。倘若μ 和S不随时的变化而变化,那么,库仑应力变化可以表示为

当ΔCFS＞0时断层面处于加载状态,触发后续地震,反之则推迟后续地震发生。研究中常用的库仑应力变化的近似表达形式

其中,μ’=μ(1-β’)为视摩擦系数,β’是斯肯普顿系数,取值范围为0.7～1.0[17],研究表明,视摩擦系数不是材料的特质,主要依靠介质的应力变化率,不同取值只影响应力变化的大小,不影响库仑破裂应力变化的空间分布[18]。在计算库仑应力变化过程中依据研究区域的背景资料确定视摩擦系数的大小,一般取0.2～0.8。本文采用汪荣江研究员开发的PSGRN/PSCMP程序计算强震的震后库仑应力变化,模拟同震响应和震后松弛效应。

2 计算模型

2.1 地壳介质模型

地壳介质模型采用分层半无限空间粘弹性模型,分为完全弹性的上地壳和中地壳、Burgers粘弹性的下地壳和上地幔。本研究中的P波速度参考赵珠等[19]的研究成果,S波速度根据求得;壳幔分层结构、地层介质密度参考王芃等[20]的研究结果;粘滞系数参考石耀霖等[21]、李艳娥等[22]的结果,下地壳的稳态粘滞系数取为1.0×1021Pa∙s,上地幔的粘滞系数取为1.0×1022Pa∙s,下地壳瞬时与稳态粘滞系数一般相差1～1.5个数量级[23,11]。因此,下地壳的瞬时粘滞系数取为1.0×1020Pa∙s,。计算库仑应力变化时的具体地壳介质模型见表1。

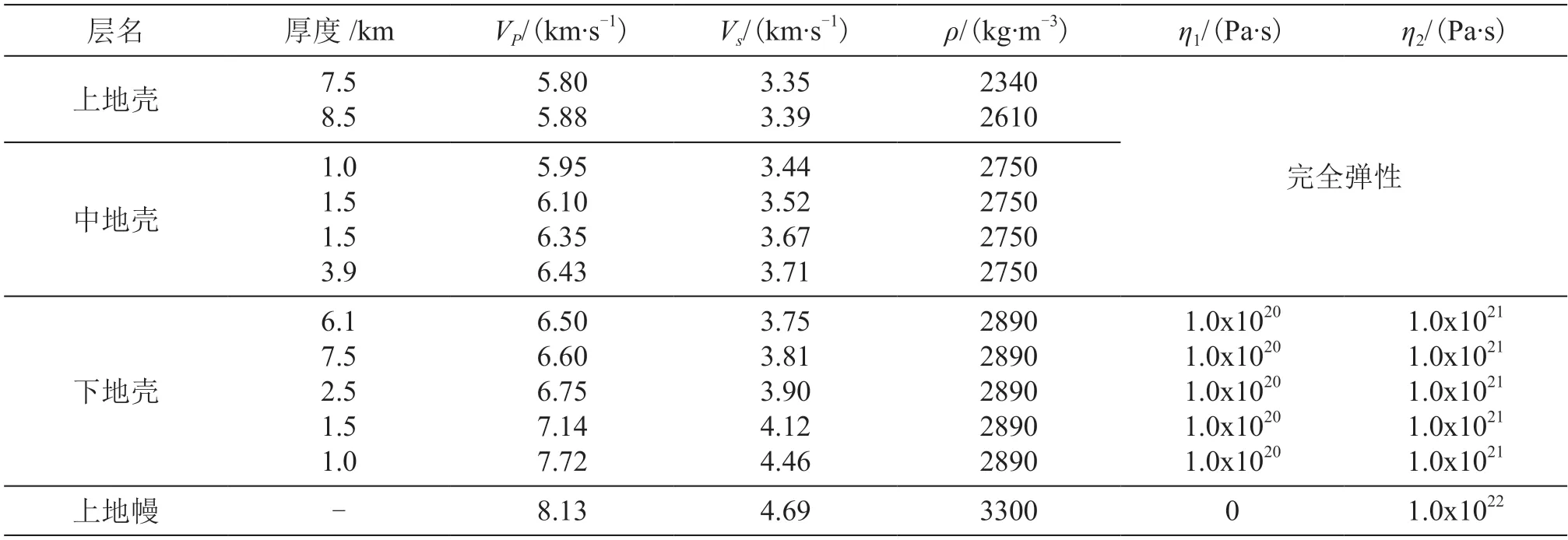
表1 地壳介质模型Table 1 Crustal medium model

图2 余震序列的震源深度分布图Fig.2 Focal depth distribution map of aftershock sequences

2.2 长宁6.0级地震的震源参数及同震位错模型

长宁6.0级地震断层参数引用台网中心的震源机制解：走向323°,倾角57°,滑动角65°。同震位错模型参数中,破裂长度和破裂宽度参考程佳等[24]经验公式,计算结果约为长28 km和宽9 km。走滑同震位错参考朱航等[25]经验公式,然后根据断层面滑动角估算出倾滑位错,计算得到走滑位错为0.638 m,倾滑位错为1.368 m。前人研究认为改变摩擦系数对库仑应力变化影响不大,本文借鉴经验取最优值为0.4[26]。

3 计算结果

3.1 同震库仑应力变化及对余震的触发作用

根据前文给出的地壳介质模型和震源参数及同震位错模型计算库仑应力变化,接收断层参数以该断层周边历史大震的破裂参数为依据,选取为走向145°,倾角90°,滑动角0°[24]。计算库仑应力变化时,计算深度是一个很重要的控制参数,余震震源深度分布如图2。采用基于粘弹性模型的PSGRN/PSCMP程序计算不同典型深度处的库仑应力变化,进而分析6.0级主震对3级以上余震的触发作用。所得结果见图3。

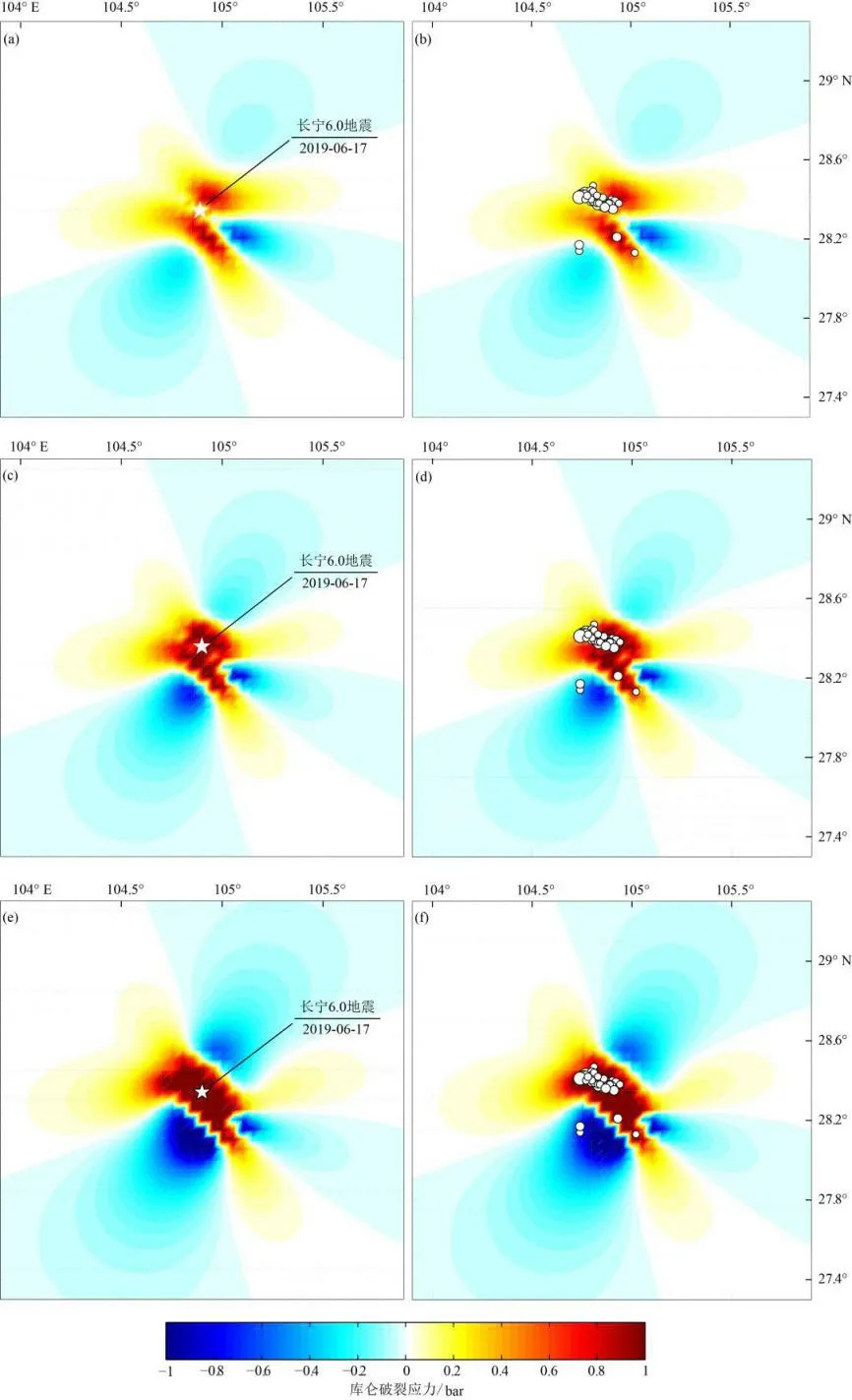
图3 不同深度处长宁6.0级地震同震库仑应力变化及对3级以上余震的触发作用Fig.3 The co-seismic Coulomb stress change of Changning M6.0 earthquake and its triggering effect on aftershocks with M≥3 at different depths

图3（a）、图3（c）和图3（e）分别为5 km深度处、8 km深度处和10 km深度处长宁地震的同震库仑应力变化,主震破裂面上的库仑应力变化分别为0.24 bar、0.9 bar和2.1 bar,均超过应力触发阈值0.1 bar,有利于触发后续地震,而且随着计算深度的增加,触发作用有一定的增强。同震库仑应力变化均呈现“蝴蝶状分布特征”,主震区的破裂方向为北西向。应力触发区主要集中在震区的北北西、南南东、北东东和南西西方向。图3（b）、图3（d）和图3（f）分别为5 km深度处、8 km深度处和10 km深度处长宁地震对3级以上余震的触发作用,不同深度计算结果均表现为64个3级以上余震中,有62个发生在库仑应力增加的应力触发区,2个发生在应力影区,综合触发率为96.9%。根据主震库仑应力变化特征可以较好地预测3级以上余震的发震地点,后续余震震中位置主要集中在震区的北北西、南南东、北东东和南西西方向。

3.2 库仑应力动态演化

研究长宁地震长时间尺度的库仑应力动态演化特征,计算不同深度处Burgers粘弹性模型同震、震后50年、震后100年以及震后200年的库仑应力变化,接收断层选取为走向145°,倾角90°,滑动角0°。计算5 km深度、8 km深度和10 km深度主震破裂面上震中位置处的不同时间尺度库仑应力变化与同震库仑应力变化的差值,结果如表2所示。以10 km计算深度为例,分析不同粘滞系数的选取对计算结果的影响,结果如图4、图5。

表2 主震破裂面上震中位置处的不同深度不同时间尺度库仑应力变化与同震库仑应力变化差值Table 2 Difference between Coulomb stress changes and co-seismic Coulomb stress changes at different depths and different time scales on the main shock rupture surface of the epicenter location

图4 粘弹性模型各个时间点库仑应力变化（η1=1.0x1018Pa∙s、η2=1.0x1019Pa∙s）Fig.4 The Coulomb stress change of viscoelastic model at various time points (η1=1.0x1018Pa∙s、η2=1.0x1019Pa∙s)

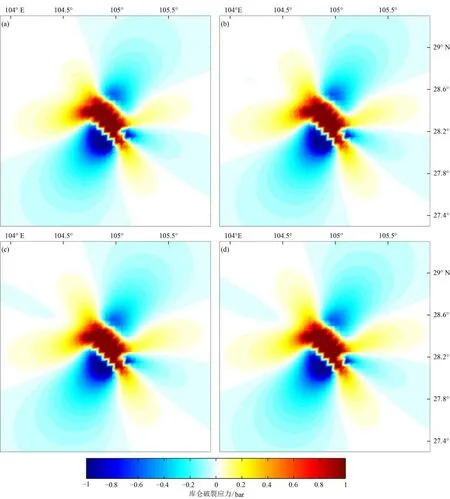
图5 粘弹性模型各个时间点库仑应力变化（η1=1.0x1020Pa∙s、η2=1.0x1021Pa∙s）Fig.5 The Coulomb stress change of viscoelastic model at various time points (η1=1.0x1020Pa∙s、η2=1.0x1021Pa∙s)

由表2可以发现,同一深度处随着时间尺度的推移,破裂面上的库仑应力变化不断增大,但幅度逐渐减小,随着计算深度的增加,库仑应力变化逐渐增加,而且随着时间尺度的推移,幅度逐渐增大。图4和图5为不同粘滞系数的Burgers模型计算得到的10 km深度处长宁地震同震响应、震后50年、震后100年以及震后200年的库仑应力变化图,均呈现“蝴蝶状”分布特征。由图4可以发现,当地层粘滞系数较小时,应力传递速度较快,小尺度时间范围内库仑应力变化幅度较大（图4（a）和图（b））,随着时间的推移,同震库仑应力变化将逐渐弛豫耗散,应力触发区和应力影区不断向外围传播,震后50年北西向出现新的应力影区（图4（b）,图4（c）,图4（d））,到达稳态所需要的时间短。图5中地层粘滞系数较大,应力传递速度慢,小尺度时间范围内库仑应力变化幅度较小（图5（a）和图5（b））,震后100年北西向出现新的应力影区（图5（c）,图5（d））,到达稳态所需要的时间更长,因而百年尺度库仑应力变化幅度较小。依据长宁地震发生至震后200年的库仑应力动态演化（图4和图5）,可以看出地震发生后应力触发区主要集中在震区的北北西、南南东、北东东和南西西方向,其他区域为应力影区。将库仑应力动态演化特征应用到本区域的地震危险性分析,重点关注上述应力触发区,可为后续余震发生提供地点依据。

4 结论和讨论

本文综合考虑同震位错和震后粘滞松弛效应,利用PSGRN/PSCMP程序计算长宁6.0地震产生的库仑应力变化,分析长宁6.0级地震的库仑应力演化特征及其对3级以上余震的触发作用。得出结论,3级以上余震发生在应力触发区的概率为96.9%,说明3级以上余震与库仑应力变化有较好应力触发关系,可以将库仑应力动态演化应用到本区地震中长期危险性预测中。粘弹性模型长时间尺度的库仑应力演化呈现“蝴蝶状”分布特征,震区北北西、南南东、北东东和南西西向均位于库仑应力增加的应力触发区,后期重点关注这些区域发生余震的可能性。

在计算库仑应力变化时,存在不确定因素和基本假设。首先,我们假定长宁6.0地震之前的累积库仑破裂应力为0;其次,建立地壳层状模型时,由于缺少本地区精细的三维速度模型及粘滞系数等参数,本文建立的模型参数均是根据前人研究成果选取的;同时对于初始应力场和长期加载场认识有限,对于库仑应力估计比较粗糙;这些都会给计算带来一定误差。虽不能准确地预测破裂时间,但根据库仑应力动态演化仍然能够为地震中长期预测提供重要信息。