MT/CSELF视电阻率影响系数及各地层贡献的初步研究
2020-03-02毛先进杨玲英
文 雯,毛先进,杨玲英,段 炜
(云南省地震局,昆明 650224)
0 前言
基于天然电磁场源的大地电磁测深用于地震预测研究已有近半个世纪[1-5];为克服天然场源信号微弱的困难,我国开展了基于大功率人工场源的极低频(CSELF)地震电磁定点观测研究[6],电磁场理论研究证明在远区观测时CSELF与MT是等价的,电磁场可以视为平面电磁波[7],其数据处理方法在原理上与MT相同。这些工作论述了MT/CSELF定点重复观测到的视电阻率资料与地震活动的关系,观测结果和深部介质导电性变化机理的研究都表明MT/CSELF是可以观测到地震前兆信息的[6,8-9]。
地震孕育过程会导致包括近地表层的地下介质电阻率变化[10],而降雨及人类生产活动一般都会引起近地表层介质电阻率变化,这种变化对地震观测而言是干扰,因此近地表层电阻率的变化既可能是孕震所致,也可能是干扰所致,或者是两种因素兼而有之。大陆内部的地震多发生在5~30 km范围,深部电性变化前兆也有可能主要出现在这一深度及其影响区域[11]。大地电磁测深具有体积效应,探测范围内各地层电阻率的变化都会对每个频点观测数据的变化有不同程度的贡献,其中近地表层的变化既可能包含孕震信息,也可能含有干扰,而且孕震信息与干扰并不容易区分,从而可能影响对观测数据中异常的确认。本文利用MT与CSELF具有的频率测深特性,定量/半定量研究不同频率下各地层电阻率变化对MT/CSELF观测到的视电阻率变化的贡献,期望有助于选择合适的电磁场频段以使易受干扰的近地表层的贡献可以忽略,以压制近地表干扰、获得地下深部电阻率变化信息。
1 影响系数及各地层贡献的计算方法简介
实践中常遇到层状地层,设MT/CSELF观测区介质电阻率分层均匀,共n层,第i层电阻率与厚度为ρi与hi,i=1,2,···,n。对于使用天然源的MT观测,或是使用人工源在远区的CSELF(极低频)观测,场源都可视为垂直地面入射的平面电磁波[7,12],根据层状大地中的平面电磁波理论,有
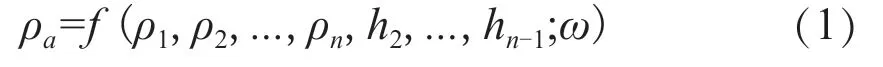
其中ρa为视电阻率,ω=2πf为电磁波圆频率,上式表明视电阻率是各层电阻率、厚度和电磁场源频率的函数。
孕震过程或其它原因使ρi(i=1,2···,n)发生变化,导致各频点观测到的视电阻率随时间变化。不妨假定观测区各层厚度不变,对式(1)两边取对数并对ρi求全微分可以得到:

式中

据层状大地的平面电磁波理论可以得到式(1)的解析表达式[12],当各层介质电阻率和厚度给定后可求得不同频率下的卡尼亚视电阻率ρa,然后采用数字方法计算出视电阻率对各层电阻率的偏微分∂ρa/ ∂ρi,并按式(3)得到各层介质的Si,这是一个成熟的正演问题,这里不赘述。
从式(2)可见,各地层电阻率发生变化时,观测到的视电阻率也将发生变化,各频点视电阻率的相对变化率等于各地层真电阻率相对变化率的加权求和Si(i=1,2···,n)为加权系数。从式(1)、(2)可知,Si既是各地层电阻率的函数,也是场源频率的函数,对同一观测场地,不同频率下Si的值是不同的;式(2)表明,当第i层电阻率的相对变化率为dρi/ρi时,该层对视电阻率的相对变化率的贡献是Sidρi/ρi,对一定的dρi/ρi,Si越大时该层的贡献或影响就越大。式(2)、(3)与地震直流电法中的影响系数理论[13-14]类似,因此本文亦将Si称为影响系数。
为方便,记各地层对视电阻率相对变化率的贡献为Gi,则
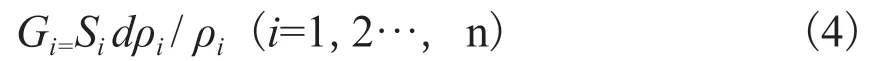
上式Si中 可以通过数值计算得到,而dρi/ρi则与介质所在层位及其电阻率变化机制有关,对于受降雨及地下潜水位波动影响的近地表层,实际资料分析表明dρi/ρi(i=1)的最大值可达90%,强震震例研究表明在200 km震中距范围类潜水层之下数百米深度范围内的地层由孕震过程引起的dρi/ρi(i>1)最大值约为10%[11,13]从加载过程中地壳内岩石裂隙的发展及孔隙水的作用等方面研究认为强地震孕育后期震源区及其周围介质电阻率可以发生大约30%到一个量级的下降变化,并得到了MT/CSELF定点重复观测结果的证明[2,5,15],利用这些数据可以估计各地层的dρi/ρi,进而可以估计各层的贡献Gi。
2 不同频率下影响系数与各地层贡献分析
大地电磁测深研究表明不同区域地壳上地幔电性结构总体上表现出“横向分块,纵向分层”特征[16-23],不同观测场点的纵向分层结构不同。下面以滇西地区一个场点为例,采用卡尼亚视电阻率定义计算影响系数,估算各地层的贡献,并分析它们随频率变化的特征。
腾冲石坪观测点[17]电阻率结构为5层,各层电阻率依次为66.07、351.10、6.20、2363.12、3.38 Ω•m,1~4层厚度依次为1.95、7.55、5.11、49.7 km。大多数情况下地下潜水位埋深0至数十米,为保守计,设地下潜水位波动及降雨的影响深度为100 m,将厚度为1.95 km的第一层拆分为二层,厚度分别为0.10 km与1.85 km,从而原电阻率结构变为6层,各层电阻率分别为66.07、66.07、351.10、6.20、2363.12、3.38 Ω•m,各层厚度依次为0.10、1.85、7.55、5.11、49.7 km。
2.1 影响系数分析
图1为腾冲石坪观测点各层影响系数随场源周期变化曲线,表1给出了几个周期点上各层影响系数及其总和的计算结果。
由图1及表1可见腾冲石坪观测点各层介质的影响系数都随周期(频率)变化,显示如下特征:①第一层影响系数S1随周期的增大而单调快速减少,该层为易受潜水位波动、降雨等影响的干扰层,定性来看,为压制这类干扰应选择在较长的周期处观测;其它各层影响系数均随电磁场源的周期起伏变化;在不超过0.02 s的短周期(高频)段S3~S6均为0,即频率50 Hz以上时第三层(顶面埋深1.95 km)及其以下介质电阻率变化对视电阻率变化无贡献,这将观测不到深部电阻率变化;②S4在158.49 s周期处达到最大值1.306,在100~200 s周期段S4远大于其余各层,第四层埋深9.5~15 km,是地震多发的层位,易于受到孕震过程的影响而发生电阻率变化,选择该周期段段将主要观测到该地层的电阻率变化。③从表1及图1可见,各层影响系数之和∑Si随周期变化而并非一个常数,这一点与直流电阻率法中无论何种观测装置下各层影响数之和等于1[14,24-27]明显不同,表1显示,MT/CSELF的∑Si在部分频点上等于1,在有些频点上大于1,而另一些频点上小于1。前文已提及,MT/CSELF影响系数的计算是一个成熟的正演计算问题,这种这出乎意料的结果并非计算方法或精度所致,其原因有待研究。
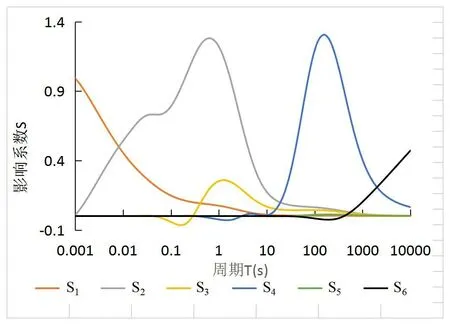
图1 腾冲石坪测点各地层影响系数—周期曲线Fig.1 Curves of the influence coefficients of each layer with the period at Shiping site in Tengchong
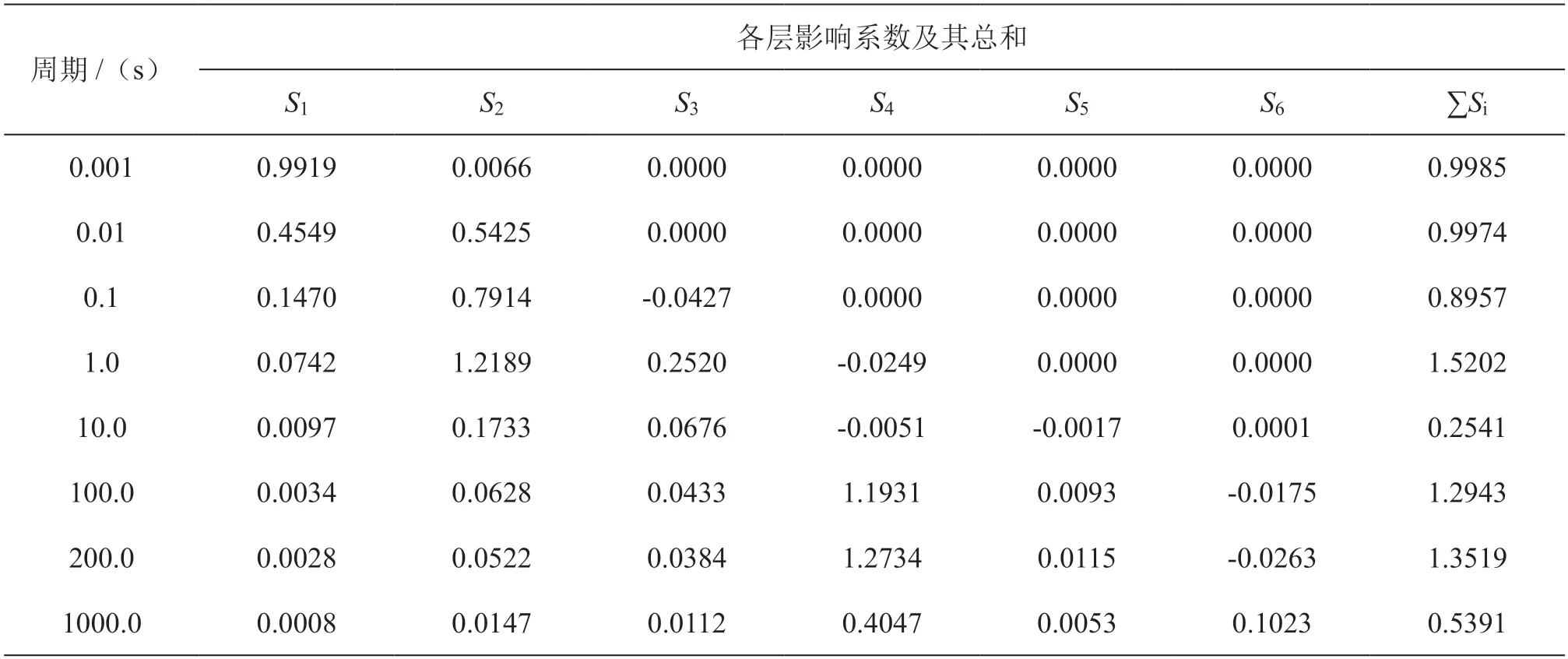
表1 腾冲石坪观测点几个周期点上各层影响系数及其总和Table 1 The influence coefficients of each layer and their sum at several periodic points at Shiping observation point in Tengchong
2.2 各地层贡献计算分析
前文已述,近地表层的变化中可能既有孕震信息也有干扰,因此地震预测中常常需要判断观测数据的变化是近地表还是深部变化所致,因此考虑近地表和深部电阻率变化同时发生时各地层贡献的数值特征是有意义的。参考前文对各层电阻率变化量级的分析结果,设在连续二次观测的间隔期间(一般不超过24 h)第一层电阻率下降2%,同时2~6层电阻率分别下降1%、1%、2%、1.5%及0%(即第6层电阻率未发生变化),总体上间隔时间越短介质物理性质变化越小,上述各层电阻率变化率大致是合理的。利用表1的影响系数值,计算相应周期点上各层的贡献Gi和视电阻率的变化率dρa/ρa,并计算即第一层的贡献在dρa/ρa中的占比),结果见表2。
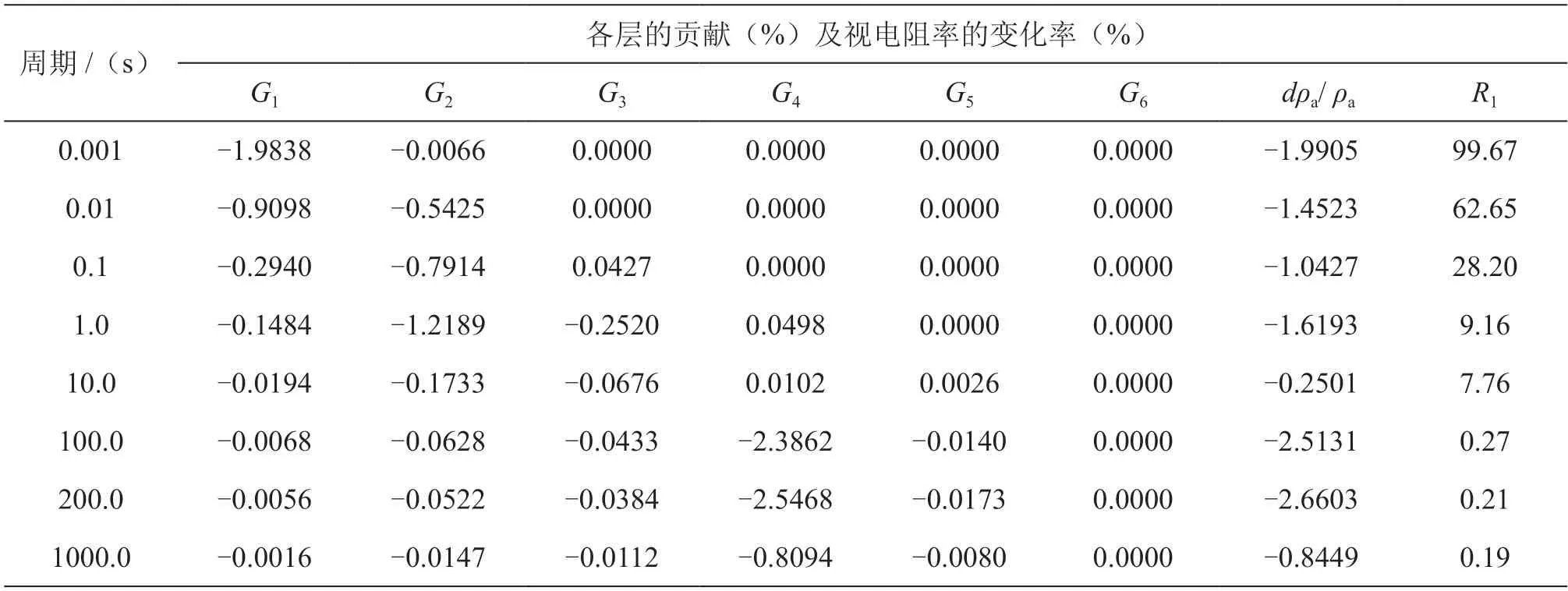
表2 近地表干扰与深部变化同时存在时几个周期点上各层的贡献及视电阻率的变化率Table 2 Contributions of each layer and the change rate of apparent resistivity at several periodic points when near-surface interference and deep changes exist simultaneously
由表2可见,在0.001~1000 s的8个周期点上,虽然视电阻率的变化率随周期起伏变化,但是第一层的贡献值随周期的增加而快速下降,其在视电阻率变化率中的占比R1也具有相同特征,这说明对于MT/CSELF的视电阻率观测而言,在适当的长周期(低频)段是有利于压制近地表层贡献的。
表2显示,在0.001 s周期点上,视电阻率下降了1.9905%,第一层的贡献在视电阻率变化率中的占比为99.67%,几乎全是该层的贡献,深部地层的贡献可以忽略;在0.01和0.1 s 2个周期点上,视电阻率分别下降了1.4523%和1.0427%,第一层的贡献在视电阻率变化率中的占比为62.65%和28.20%,该层的贡献也很明显。若在0.001~0.1 s周期范围观测,在分析视电阻率变化的原因时,就难以排除近地表层中的干扰因素,也就难以确定前兆异常。
从表2清楚地看到,在100~1000 s的3个周期点上,视电阻率分别下降了2.5131%、2.6603%及0.8499%,第一层的贡献在视电阻率变化率中的占比分别为0.27%、0.21%及0.19%,这表明此周期段近地表层的贡献可以忽略不计,之所以这样,从表2可见是因为在此周期段S1(第一层的影响系数)相比于∑Si(影响系数之和)以及其它各层的影响系数Si(i=2~6)都小得多。因此,无论近地表层干扰存在与否,在分析视电阻率变化的原因时都可以排除干扰的影响,从而可以确定前兆异常。
另外表2还显示,在100~1000 s周期段,不仅近地表层的贡献G1可以忽略不计,而且G4(第四层的贡献)远大于其它各层,该层埋深9.5~14.61 km,处于地震多发层,该频段有利于观测到地震前兆。
从公式(1)、(3)已知视电阻率及影响系数都是各层电阻率及频率的函数,因此不同电阻率结构的观测点各地层影响系数随频率变化的曲线形态也不同,但计算表明近地表层及深部各层影响系数和各层贡献随频率变化都具有上述基本特征,因篇幅所限不再举例。
3 结论
MT/CSELF具有探测深度大、探测深度方便调节、观测站占地面积小、易于测点选择与建设以及观测环境保护等许多优点,在地震前兆观测中必将发挥越来越重要的作用。出于压制近地表干扰、有效获取深部电阻率变化,从而有利于确定异常的目的,在水平分层均匀电阻率结构场地条件下本文研究了MT/CSELF视电阻率影响系数和各地层对观测数据变化率的贡献,主要得出如下认识:
(1)各地层视电阻率的变化对MT/CSELF视电阻率的变化率有不同程度的贡献,贡献的大小与影响系数成正比,而各地层影响系数都随电磁场源的周期(频率)变化。
(2)对于较薄(厚度100 m左右)的易受干扰的近地表层,其影响系数和对MT/CSELF视电阻率变化的贡献随周期的增加快速下降,在特定的短周期段(其值取决于电阻率结构)只有近地表层对观测到的视电阻率变化有贡献而之下各层无贡献;近地表层之下各层的影响系数及它们对视电阻率变化的贡献则随电磁场源周期起伏变化,各自在不同的周期处(其值也取决于电阻率结构)取得最大值。
(3)对不同的层状电阻率结构的观测场地,通过影响系数和各地层贡献分析,可以确定合适的长周期段,在此周期段观测可以使得近地表层对视电阻率变化的贡献忽略不计,视电阻率变化主要反应深部各层的电阻率变化,从而有利于确定前兆异常。
(4)发现MT/CSELF各层影响系数之和随周期变化而并非常数,它在部分周期点上等于1、部分周期点上大于1,而在部分周期点上小于1,这是出乎意料的,其原因有待研究。
