《概率论与数理统计》教材中引入MATLAB辅助教学的探究①

何小年 彭琼

(湖南涉外经济学院信息与机电工程学院 湖南长沙 410205)

概率论与数理统计是工科专业开设的一门数学基础必修课程。本课程也是支撑人工智能发展的基础数学课程之一,其涉及的多个知识点（如：中心极限定理、参数估计、假设检验等），皆源自实际应用需求。如何利用软件为本课程教学服务，实现将这门课程与实际应用相结合，并超越过去侧重于讲解课程概念的传统教法，培养学生通过编程解决实际问题的能力，满足工科后续课程的需求，是任课教师最关心的问题之一。

“复旦共识”、“天大行动”和“北京指南”意味着我国正式拉开新兴工科（Emerging Engineering Education/3E，简称新工科）建设大幕。所谓新工科，是指以立德树人为引领，以应对变化、塑造未来为建设理念，以继承与创新、交叉与融合、协调与共享为主要途径，培养未来多元化、创新型卓越工程人才[1]。新工程中的创新工程教育方式与手段，提出充分利用仿真等技术作为创新工程实践教学方式，对于推进信息技术和教育教学深度融合、提高教学效率，有极大的促进作用。选用合适的计算和仿真软件辅助教学，对于助推概率论与数理统计课程成为新工科教育的一分子，至为重要。

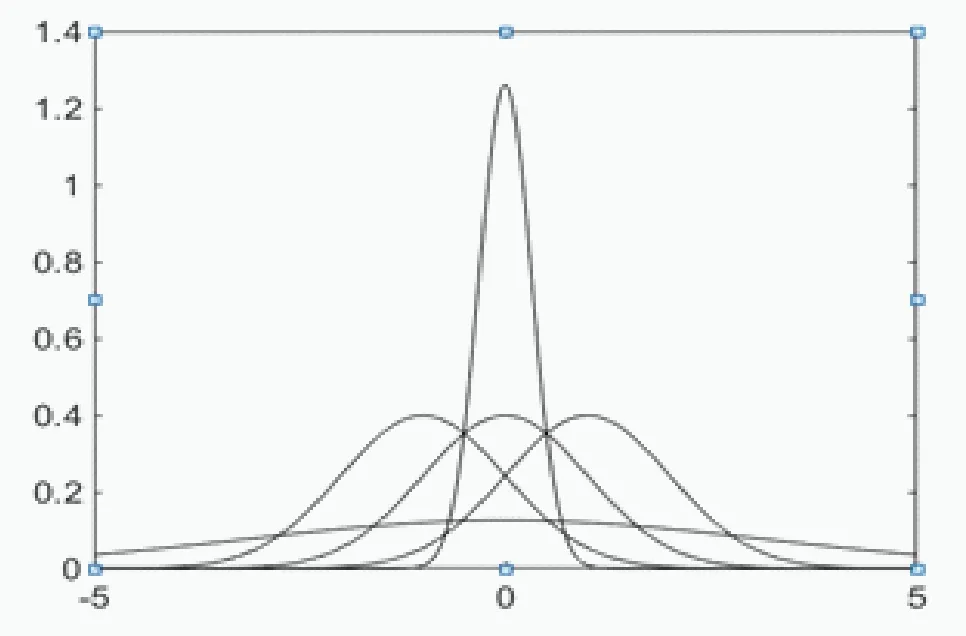
图1 概率密度函数图

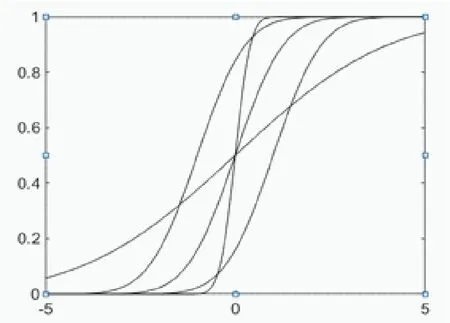
图2 为分布函数图

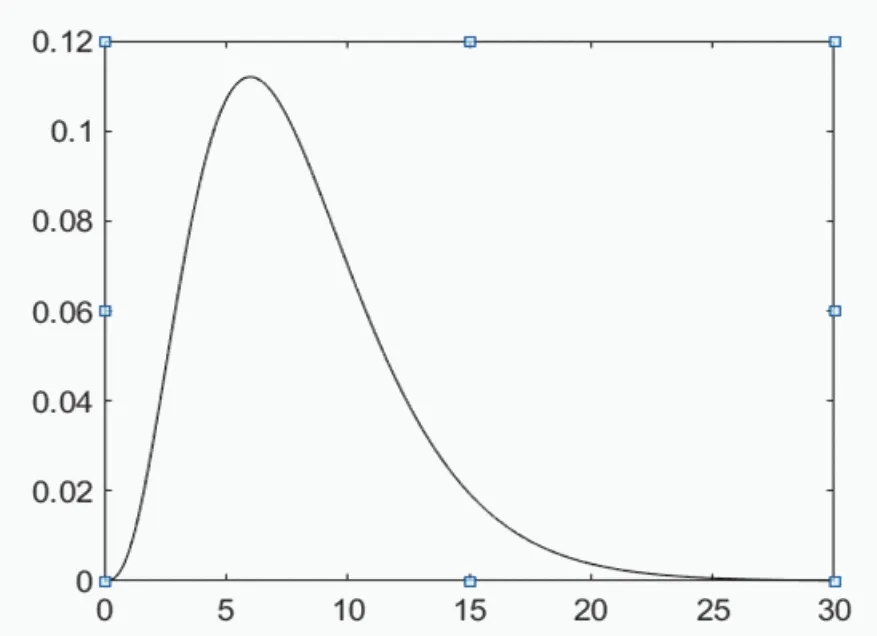
图3 卡方分布的密度函数图形

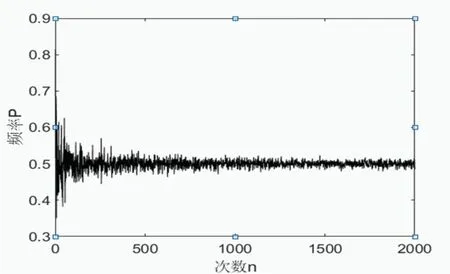
图4 模拟抛硬币实验

MATLAB是一个交互式的以矩阵计算为基础的科学和工程计算软件，它将计算、可视化和编程功能集成，非常便于使用。概率论与数理统计课程引入MATLAB辅助教学，便于组织专业工程案例来提高学生的学习兴趣和学习效果，有助于进一步培养学生的数学思维能力，有利于学生提高学生利用数学建模解决复杂工程问题的能力，从而切实提高人才培养质量，为工科专业学生的培养打下坚实的数学基础。此外，学生掌握了MATLAB语言，将MATLAB语言更好地融入后续课程，包括电路、信号与系统、自动控制、数字图像处理等课程等，能为学生后续学习这些课程创造条件，特别是能帮助学生在学习这些课程的时候开展创新性研究与实验。

如何利用Matlab辅助概率论与数理统计课程教学，在中国知网查询，最早的研究文献系伍善敏2002年发表于广西师范学院学报。至今有30余篇。周后卿展示了MATLAB、EXCEL、SPSS等在课程教学中的作用[2]；解博丽等用实例说明了MATLAB在概率论与数理统计中的绘制曲线功能以及数值计算功能,体现出其直观性和简便性[3]；张福鼎结合概率论与数理统计教学中常见的问题,讲述如何通过Matlab软件理解数学过程[4]；杨柳讲述案例教学法运用于高校《概率论与数理统计》教学中，可以直接将理论转化为实际[5]；秦丽娟等探讨应用R软件辅助概率统计教学的可行性，为概率统计课程教学改革提供参考[6]。本文就如何将以MATLAB软件辅助概率论与数理统计教学进行初步探索。

1 引入MATLAB的情景及示例

将MATLAB软件引入概率论与数理统计课堂教学，可以吸引学生的注意力，激发学生学习本门课程的热情，提高教学效果。此外，学习MATLAB有助于学生在后续的专业课学习。下面用典型例题来展示MATLAB软件在求概率论与数理统计相关问题中的便利性和直观性。

例1：分别绘制出（μ，σ^2）为(-1,1),(0,0.1),(0,1),(0,1 0),(1,1)时正态分布的概率密度函数与分布函数曲线。

需在MATLAB软件的Command Window窗口输入如下内容：

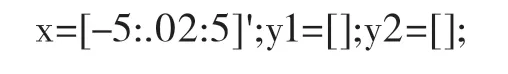
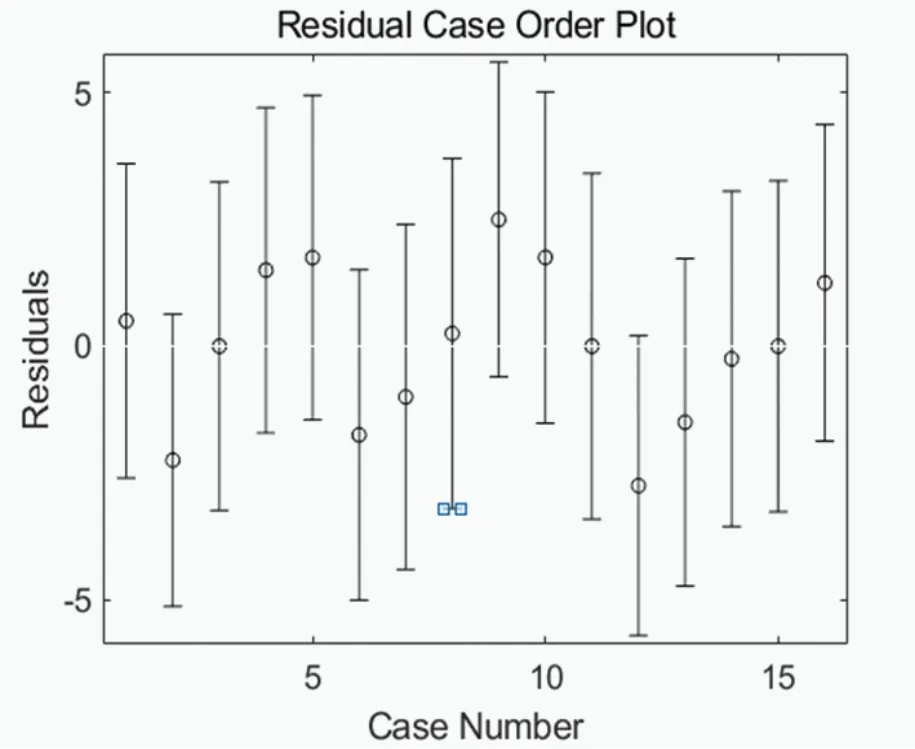
图5 残差分析图

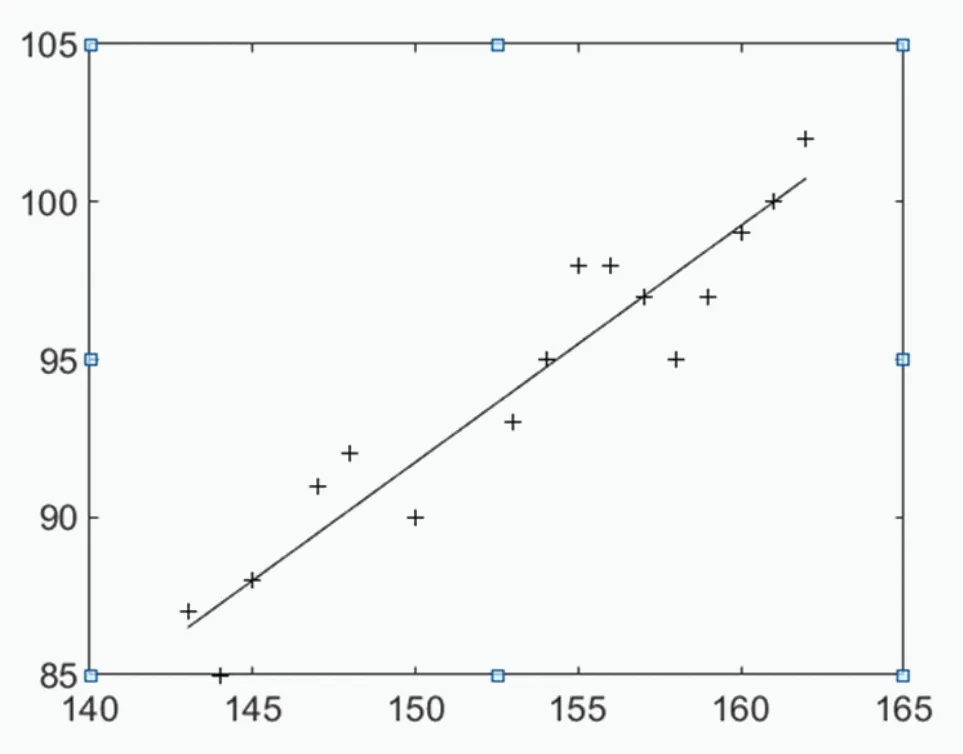
图6 拟合曲线图

表1 女子身高和腿长 单位：cm

输出结果如下：图1是概率密度函数图，图2是分布函数图。

例2：求标准正态分布随面变量X落在区间(-∞，0.4)的概率。

在MATLAB软件的Command Window窗口输入如下内容：

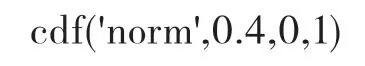
输出结果：

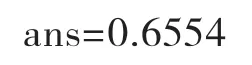
例3：计算自由度为8的卡方分布，在点2.18处的密度函数值，并绘制卡方分布的密度函数图形。

在MATLAB软件的Command Window窗口输入如下内容：

输出结果：

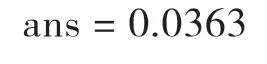
卡方分布的密度函数图形如图3所示。

例4：模拟抛硬币实验

在MATLAB软件的Command Window窗口输入如下内容：

输出结果如图4所示。

例5：模拟掷骰子实验

在MATLAB软件的Command Window窗口输入如下内容：

输出结果：

掷骰子1朝上的次数是1667280，频率是0.166728

掷骰子2朝上的次数是1667028，频率是0.166703

掷骰子3朝上的次数是1666868，频率是0.166687

掷骰子4朝上的次数是1665663，频率是0.166566

掷骰子5朝上的次数是1666995，频率是0.166700

掷骰子6朝上的次数是1666166，频率是0.166617

例6：一元线性回归测得16名女子的身高和腿长如表1所示。

试分析这些数据之间的关系。

在MATLAB软件的Command Window窗口输入如下内容：

输出结果：

接着进行残差分析输入：rcoplot(r,rint)；显示结果如图5所示。

最后进行预测及作图输入：

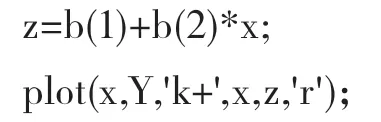
显示结果如图6所示。

其中方程常数B0=-20.7500,变量系数B1=0.7500，置信区间是[-42.1526,0.6526]和[0.6105,0.8895],R的平方为0.9047，F为132.8768，P为0.0000，其中R的平方越接近于1代表回归模型越准确，P＜0.5也代表Y=-20.7500+0.7500X方程成立。

通过上面6个实例，我们可以看出，MATLAB在求解概率论与数理统计典型问题中具备简单易学、功能强大、直观、运算速度快等优势，可以大大减少学生烦琐的计算过程，既能够提高学生的动手能力，又能够激发学生的学习兴趣，从而达到较好的教学效果。

2 结语

在概率论与数理统计课程教学中引入MATLAB进行辅助教学，有助于学生在后续的专业课学习，通过仿真模拟演示，为学生提供直观认识，解决了课程中概念抽象不直观、难理解的难题，可以加深学生对知识的理解，提高学生解决实际问题的能力，实现了复杂问题简单化，对于激发学生学习兴趣、加强理论分析与实际问题之间的联系，具有重要的作用。