仿生正弦前缘对翼面动态失速的影响

2020-03-02侯宇飞李志平

航空学报 2020年1期

侯宇飞，李志平

1. 北京航空航天大学能源与动力工程学院，北京 100083 2. 北京航空航天大学航空发动机气动热力国家重点实验室，北京 100083 3. 北航(四川)西部国际创新港科技有限公司，成都 610200

直升机在前飞状态下为了平衡桨盘升力，需增大后行桨叶迎角。在高速前飞、重载飞行等典型工况下, 剧烈变化的迎角将造成桨叶动态失速。失速桨叶最大升力系数显著提高，但强烈的非定常分离和气动载荷变化是振动的来源，不仅严重限制直升机飞行包线还降低了结构寿命，还可能引发附加的气动阻尼[1]。因此，有效控制动态失速是改善旋翼流动特性和提升直升机飞行性能的关键。

翼型气动载荷的剧烈变化与前缘分离涡的产生、发展和脱落关系密切。当翼型上仰超过静态失速迎角后，分离涡在前缘上表面形成并快速向下游移动，旋涡的低压效应使升力增加，随后作用于尾缘造成低头力矩激增，当旋涡脱离翼型表面，升力骤降。针对这种前缘分离涡目前已经发展出一系列控制方法，主动控制有下垂前缘[2]、固定前缘条[3-4]、前缘喷气[5]、后缘小翼[6]。尽管它们在抑制分离涡方面取得了不错效果，但动态控制装置势必造成结构复杂，重量增加，生产和维修成本上升[7]，相比而言被动控制实施难度更小。

近年来，座头鲸胸鳍前缘的凸起引起学者们极大兴趣。作为一种被动控制，突起前缘显著增强了座头鲸的机动性，使其形成独特的180°U型回转捕食方式[8]。大量静态研究表明，前缘突起能够在高迎角下提高升力，推迟失速。Watts和Fish[9]应用小板理论对翼面进行数值模拟，表明凹凸前缘在10°迎角下升力增加4.8%，阻力减小10.9%。Miklosovic等[10]通过风洞试验发现凹凸前缘翼面在雷诺数Re=5×105下失速迎角增大40%，最大升力提高6%。关于流动机理，学者普遍认为前缘凸起类似于涡流发生器[11-13]，其产生的高强度流向涡增强了边界层与主流区域的动量交换，是增加升力和推迟失速的关键，Stanway[14]运用粒子图像测速(PIV)法技术证实了这一点，发现在大迎角下前缘波峰间形成了沿流向的反向涡对。同时流向涡产生的下洗流动[15-16]促使流动贴附在翼型上表面，因而推迟失速。此外，文献[8，11]还提出这种凸起结构相当于翼刀，抑制了分离区沿展向传播。目前关于将仿生凹凸前缘运用到动态失速控制的研究较少，Borg[17]通过试验研究了雷诺数为1.3×105下不同凹凸前缘对NACA0012动态失速特性的影响，发现减小凸起间距和凸起幅度能够增大升力峰值，减小迟滞效应。在雷诺数为1×106下[18]，波状凸起前缘同样提升了NACA0012动态失速平均升力。文献[17]只研究了仿生凹凸前缘对气动载荷的影响，没有进行流动机理分析。文献[18]旨在提高动态失速下机翼的升力，未考虑凹凸前缘对阻力和俯仰力矩的影响，并且未讨论凹凸几何参数对流场的作用。

鉴于凹凸前缘在直升机旋翼动态失速控制方面的潜力，为了将其应用在工程实践中，有必要深入理解凹凸前缘流动控制机理。本文基于试验验证的数值模拟方法，研究了仿生前缘对翼面动态失速的抑制作用，重点关注对分离涡的影响机理，对比了不同前缘几何的气动特性。同时为了探究仿生前缘的作用范围，讨论了平均迎角、迎角振幅、折算频率以及来流马赫数对其动态失速控制效果的影响。

1 几何模型与数值方法

1.1 仿生凹凸前缘造型

选取SC1095旋翼翼型为研究对象，它被应用于美国黑鹰直升机主桨，分布在0.85R(R为桨盘半径)以外展向位置，是动态失速经常发生的区域。原型翼由SC1095翼型沿桨叶展向无扭转拉伸而成，展长为0.5倍翼型弦长。采用正弦函数模化仿生凹凸前缘，翼面弦长沿展向的分布为

C(z)=C+Acos(2πz/λ)

(1)

式中：z为展向坐标；C(z)为翼面展向各截面弦长；C为原型翼弦长；A为正弦前缘波峰；λ为正弦前缘波长。

参考座头鲸胸鳍前缘外形[19]，A分别取0.025C、0.050C和0.100C，λ分别取0.25C和0.50C，3种波峰和2种波长组合生成6种正弦前缘翼作为研究对象。图1给出了原型翼和正弦前缘翼示意图，经验证[18]当两侧设为周期性边界条件时，展向的正弦周期数目不影响计算结果，因此为减少计算量本文正弦前缘翼沿展向均取1个周期。为保证只有翼面前缘做正弦修型而不改变其他区域几何，翼面尾缘沿展向对齐，只对前缘(最大厚度之前)进行缩放处理(见图2)，其表达式为

(2)

ynew=yoriginal

(3)

式中：x为横坐标；y为纵坐标；“original”代表原型翼；“new”代表正弦前缘翼；“mt”代表原型翼最大厚度位置；坐标原点位于尾缘。

图1 原型翼和正弦前缘翼俯视图Fig.1 Top view of prototype wing and sinusoidal leading-edge wing

图2 翼型前缘缩放示意图Fig.2 Schematic diagram of scaling of airfoil leading-edge

1.2 网格生成与数值方法验证

为确保计算结果不受边界条件影响，计算域取100倍弦长(如图3所示)。计算全部采用结构网格，同时在翼型周围方形区Ⅰ及尾迹区Ⅱ进行网格加密处理, 通过拉伸生成展向网格。定义全部网格做整体刚性俯仰运动来模拟动态失速，不仅能够保证网格质量不变，还避免了使用动静交界面产生的数据传递误差。所有外场边界定义为同一个速度进口边界，因而转动到任一迎角时进口面积始终等于出口面积。在满足总体质量连续的情况下，使用唯一速度同时定义进/出口是可行的[20]。翼型表面为无滑移条件，展向两侧为周期性边界条件。如图4所示，翼型附近采用O型网格，表面第1层网格高度使y+最大不超过2。

验证案例取自文献[21]的试验结果，Re=3.92×106，马赫数Ma=0.3，翼型以折算频率k=0.1做正弦俯仰, 转轴在距前缘25%弦长处。采用3种不同数目的网格来验证网格无关性，分别为64万、160万和288万。为及时捕捉失速涡的发展动态，将1个俯仰周期分为1 000个时间步。假设流动为完全发展的湍流，考虑到Spalart-Allmaras(S-A)模型和k-ωSST(Shear Stress Transport)模型在预测翼型动态失速方面都有广泛应用，这里对二者计算结果进行了比较。采用压力基求解器，搭配Coupled算法。相比于Simple和Piso算法，Coupled算法能更快达到收敛，尤其对长时间步具有较高鲁棒性[22]。下文以CL表示升力系数，CD表示阻力系数，Cm表示俯仰力矩系数,α表示迎角。参考长度为弦长，参考面积为弦长×展长，俯仰力矩参考点为转轴处。

图3 计算域示意图Fig.3 Schematic diagram of computational domain

图4 翼型附近的O型网格Fig.4 O-block mesh around airfoil

图5给出了验证案例计算结果，通过对比试验结果，看到在上行(迎角增大)过程中，两种湍流模型均能准确地预测气动载荷，包括失速迎角和升力系数峰值。但是在下行(迎角减小)过程中，计算结果与试验值有一定偏差，这与分离后的湍流具有强非平衡性有关，而模型参数由简单流动获得。S-A模型在失速迎角附近预测的气动性能出现大幅振荡，且计算得到的抬头力矩峰值和低头力矩峰值较于k-ωSST偏差更大，因此采用k-ωSST模型。中等密度网格结果已不受网格数目增加的影响，在下文的计算中均采用中等数量网格。总体可见，本文采用的数值方法能够模拟动态失速。

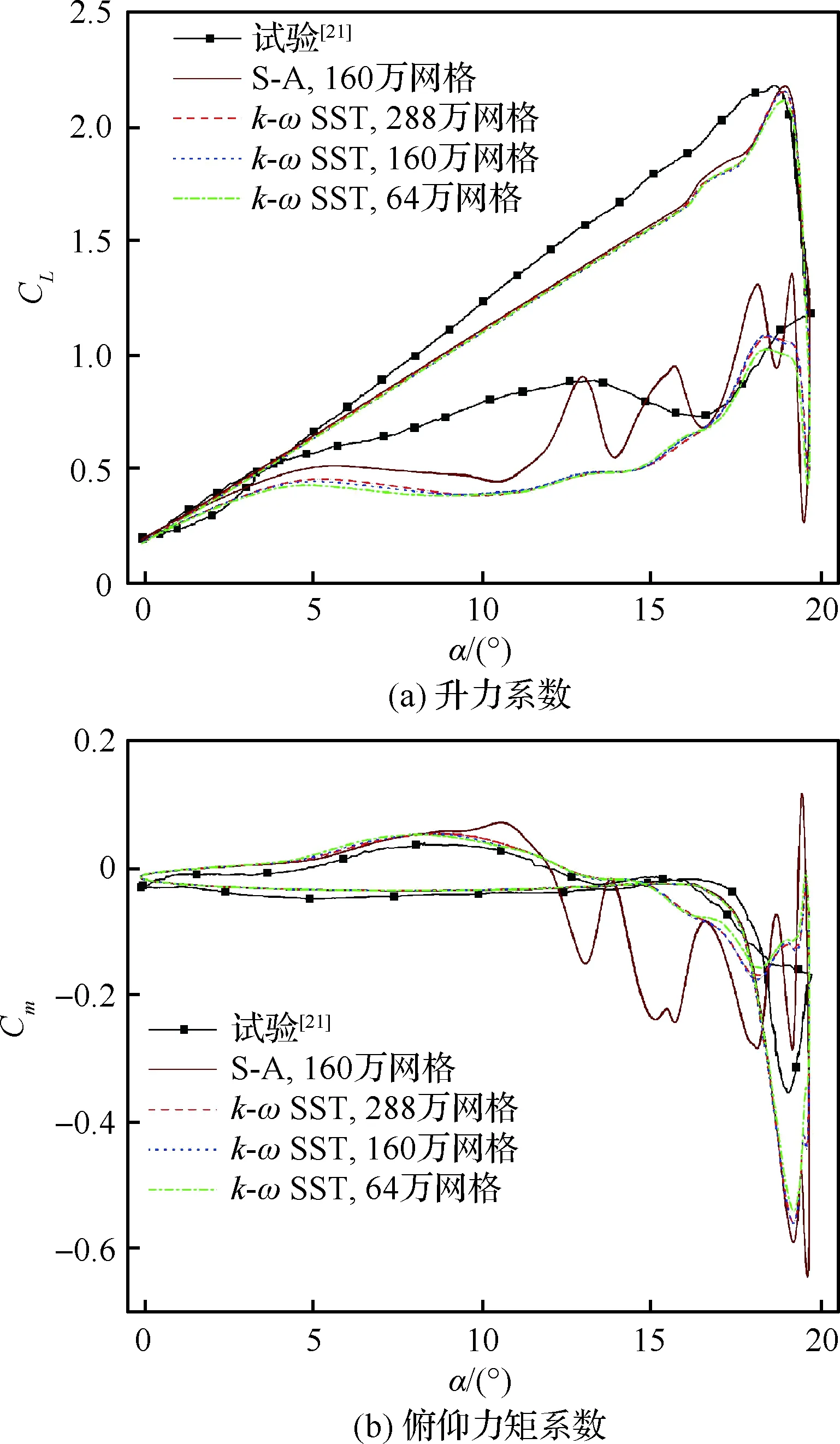
图5 计算值与试验值的对比Fig.5 Comparison between calculated and experimental values

2 仿生前缘动态失速控制机理分析

针对1.2节中案例，表1列出了6种仿生正弦前缘翼的几何参数与计算结果，包括最大升力系数CLmax、最大阻力系数CDmax、最大俯仰力矩系数Cmmax相较于原型翼的变化量(ΔCLmax、ΔCDmax和ΔCmmax)。仿生前缘在减小载荷幅值方面展现出巨大潜力，6种造型均能显著降低阻力峰值和低头力矩峰值，这对降低振动载荷和增加桨叶寿命很有必要。尽管都伴有不同程度的升力损失，但急剧变化的俯仰力矩是动态失速中最严重的问题，是颤振边界的成因，而一定的升力峰值减小可以接受，这是因为直升机在高前进比下升力主要由前后侧桨盘60%～85%半径区域产生，而动态失速通常发生在左侧桨盘85%半径以外区域[23]。可以看到随着波峰的增加和波长的减小，阻力和力矩峰值减小量增加，但升力系数损失也有所增加。其中A025W5、A05W5和A025W25以较小的升力代价获得了明显的阻力特性和力矩特性的提升。

表1 正弦前缘翼案例及结果汇总

本节以A05W5为例，对比原型翼分析其动态失速控制机理。当迎角分别上行至8.49°、10.35°和11.89°时，CL均保持线性增长(如图6(a)所示)，流动附着于翼面。各截面压力系数(Cp)对比由图7给出，Original代表原型翼截面，Peak代表波峰截面，Trough代表波谷截面。随着迎角增加，原型翼吸力峰值有所增加，而波谷截面吸力峰值显著增加，在迎角为11.89°时Cp超过了-10，这是因为部分气流从波峰向波谷汇聚，速度增加形成了高负压区和强逆压梯度。反过来，一部分将要抵达波峰的气流被波谷前缘的负压抽取过去，使得波峰前缘绕流加速效果减弱，因此波峰截面Cp峰值始终较小。

图6 原型翼与仿生翼A05W5气动系数对比Fig.6 Comparisons of aerodynamic coefficients between original wing and bionic wing A05W5

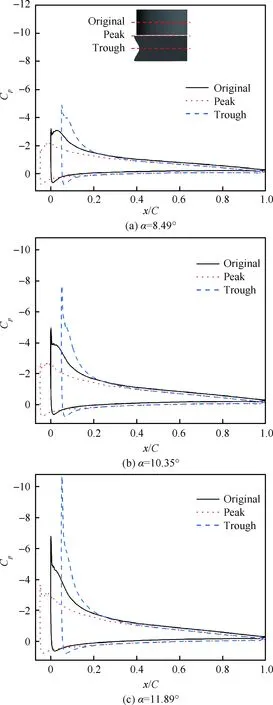
图7 不同截面压力系数对比Fig.7 Comparisons of pressure coefficients on different sections

图8和图9给出了迎角上行至12.8°时的各截面压力系数分布和流场，此刻A05W5的CL增长率发生了变化，原型翼CL仍位于线性增长区。流经波谷的气流在更短的行程内升压至平均水平，产生的强逆压梯度使波谷更易分离，提前出现了分离涡，其附带的的低压效应使得波谷截面Cp出现“小平台”，进一步增加了波谷截面翼型的升力，从而改变CL斜率，这与Carr等[24]的结论一致。原型翼与波峰截面均保持附着流动。

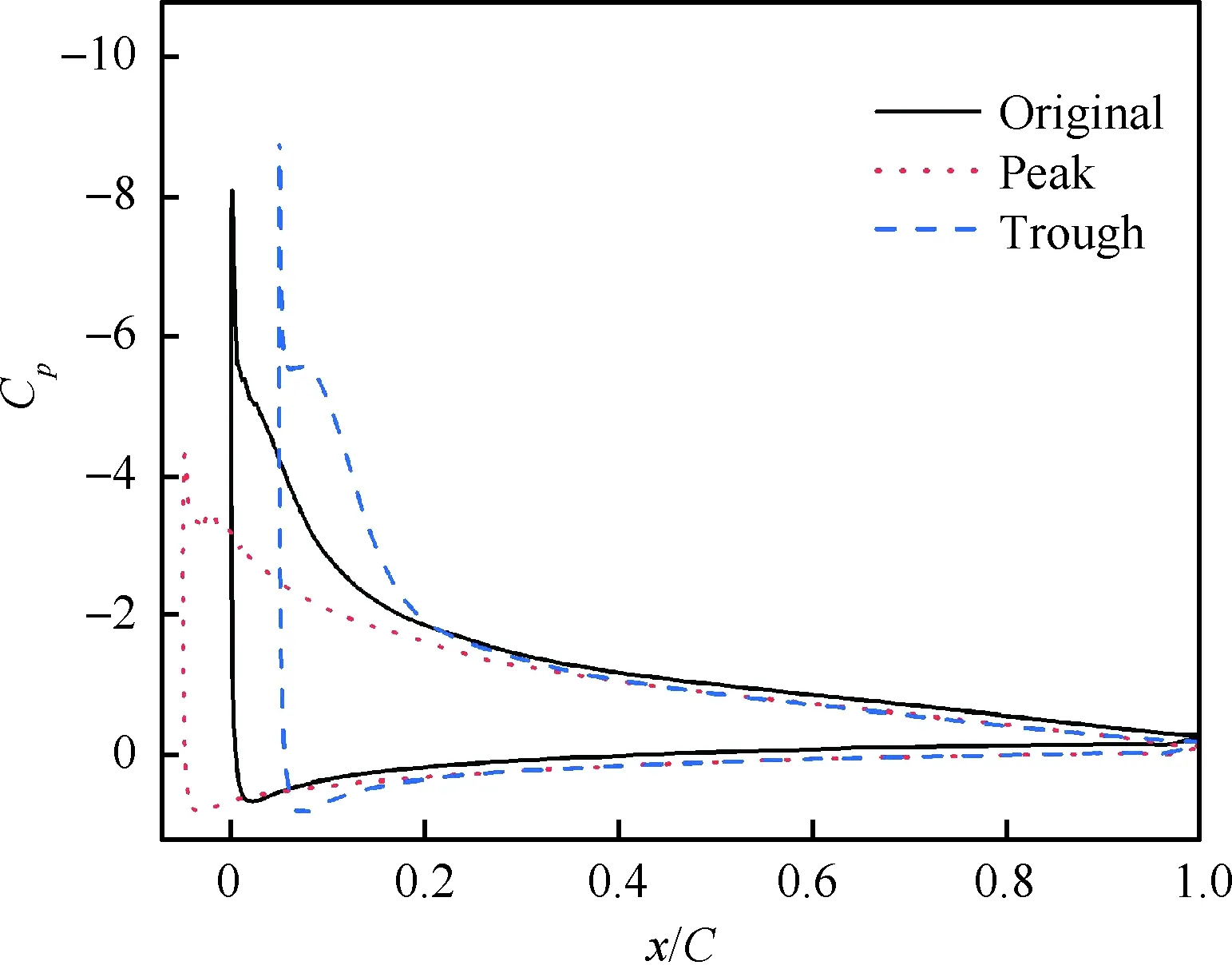
图8 α=12.8°时不同截面的压力系数Fig.8 Pressure coefficients on different sections at α=12.8°

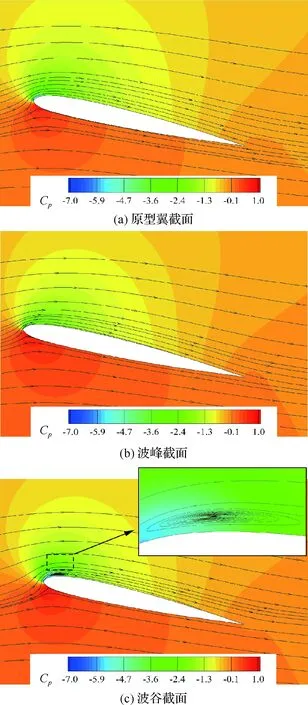
图9 α=12.8°时不同截面的流场Fig.9 Flow fields on different sections at α=12.8°

图10和图11展示了迎角上行至16.05°时的各截面压力分布与流场。原型翼CL增长率出现变化，较于A05W5推迟了约3.3°，同样在脱离CL线性增长区时观察到前缘分离涡。然而波谷在α=12.8°时产生的分离涡更早进入下游，覆盖了约60%波谷截面上表面，从Cp曲线图看出分离涡形成的低压区向下游移动，升力继续增加，压差阻力和低头力矩同时增大。波峰截面流动基本附着，但因为受到波谷分离涡牵动，波峰截面尾缘上游流线扭折，出现回流和展向流动，被牵动的气流在一定程度上限制了分离涡的发展。

图10 α=16.05°时不同截面的压力系数Fig.10 Pressure coefficients on different sections atα=16.05°

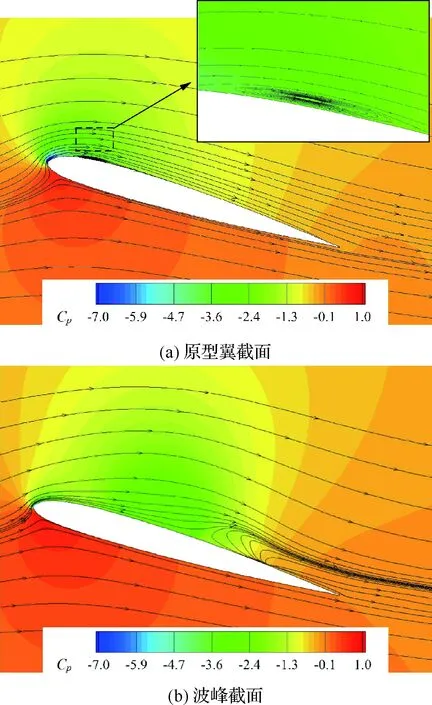
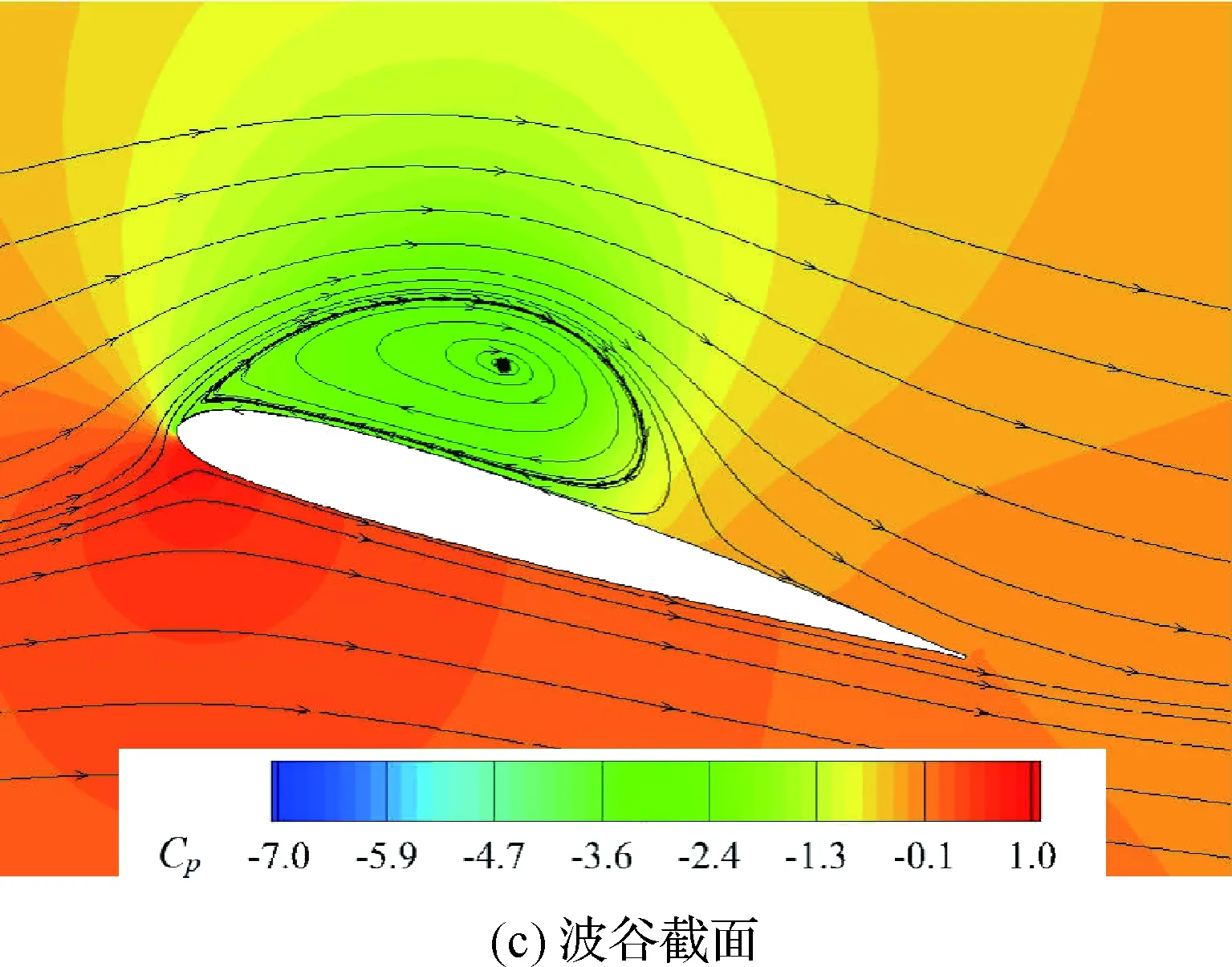
图11 α=16.05°时不同截面的流场Fig.11 Flow fields on different sections at α=16.05°

迎角上仰至18.85°，Cp曲线及流场如图12和图13所示。原型翼CL接近峰值，分离涡几乎覆盖上表面，随该涡向下游移动，低压区后移，Cp峰值减小。与同处CL峰(α=16.05°)的A05W5流场相比，原型翼分离涡更强，所产生的低压区造成更大的压差阻力及俯仰力矩，同时也是CL峰高于A05W5的原因。A05W5此刻已经失速，主分离涡开始脱离上表面，低速回流区覆盖了波谷截面和后半波峰截面。

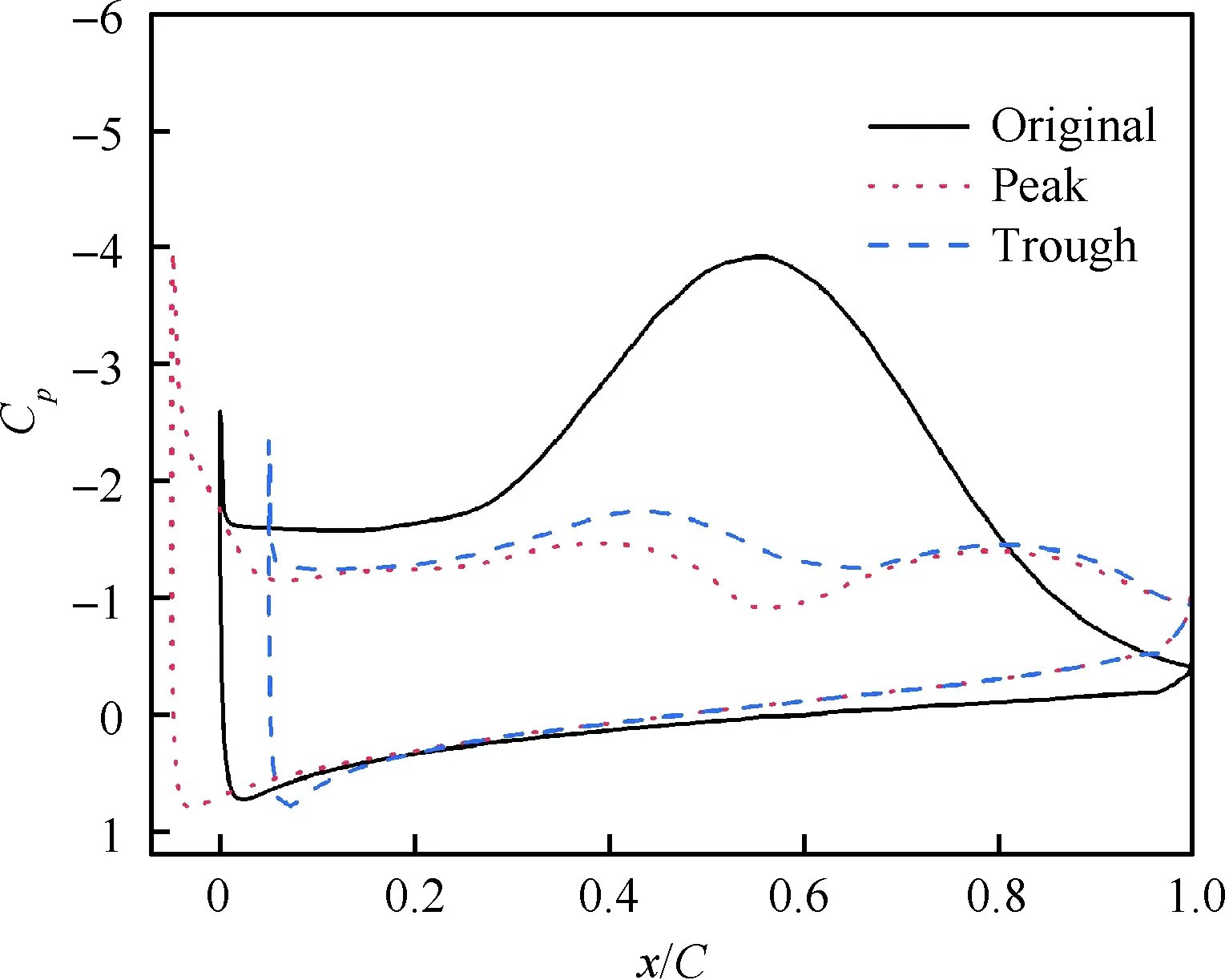
图12 α=18.85°时不同截面的压力系数Fig.12 Pressure coefficients on different sections atα=18.85°

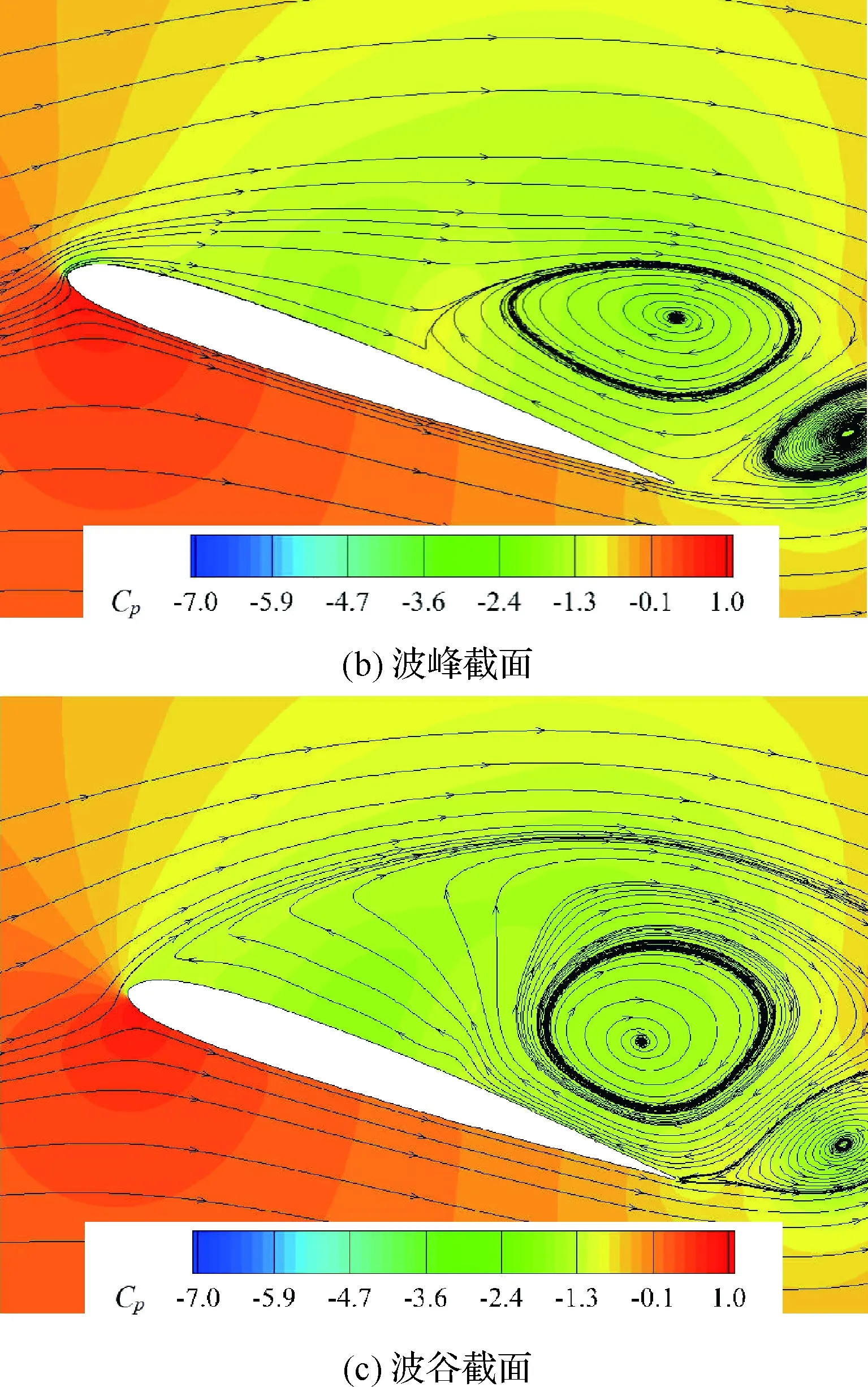
图13 α=18.85°时不同截面的流场Fig.13 Flow fields on different sections at α=18.85°

图14和图15给出了最大迎角19.68°时的Cp曲线图和流场。由于分离涡与其低压区逐渐远离以及涡诱导速度损失，原型翼CL骤降。同时分离涡在尾缘卷起的逆时针涡形成低压区，导致低头力矩高于A05W5，而A05W5尾缘涡此刻早已脱落(见图15(b)和图15(c))。即使在最大迎角，波峰截面前半区域仍然不存在分离涡，流动继续附着在翼型表面，在一定程度上充当“翼刀”限制了分离涡展向传播。另外，原型翼产生了二次前缘分离涡与逆时针涡结构，破坏了附着流，但这种反向涡对并未出现在仿生翼周围。

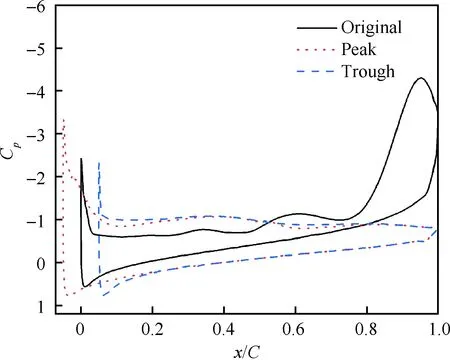
图14 α=19.68°时不同截面的压力系数Fig.14 Pressure coefficients on different sections atα=19.68°

图15 α=19.68°时不同截面的流场Fig.15 Flow fields on different sections at α=19.68°

随后迎角开始下俯，两种翼型的气动系数呈现出不同变化趋势。结合图6看到原型翼的CL、CD和Cm都先回涨再骤降，而A05W5的气动载荷始终平稳减小。图16和图17展示了迎角下俯到19.1°时的Cp曲线图和流场。此刻原型翼CL回涨至高点。因为图15(a)中的二次前缘分离涡Ⅰ向下游移动并增强，Cp峰值增加，升力增加，阻力和低头力矩随之增加。在图15(a)中与该二次前缘涡成对出现的逆时针涡Ⅱ几乎消散，从而看到涡Ⅰ与已经弱化的主分离涡连在一起(见图17(a))，随着迎角进一步减小，二次分离涡的脱落造成CL再次陡降。与之对比，A05W5并未出现二次分离涡的发展和脱落。

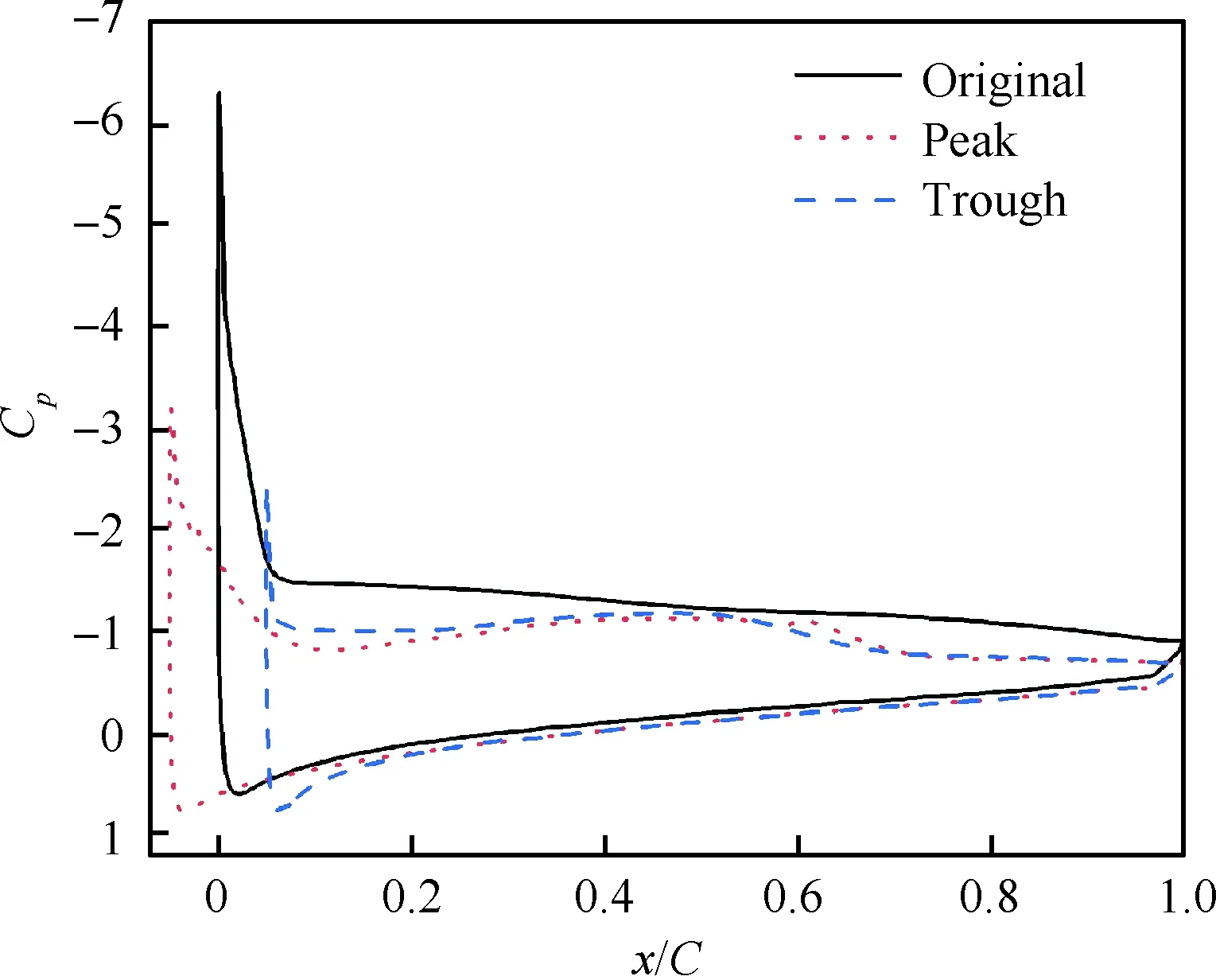
图16 α=19.1°时不同截面的压力系数Fig.16 Pressure coefficients on different sections atα=19.1°

图17 α=19.1°时不同截面的压力系数Fig.17 Pressure coefficients on different sections atα=19.1°

综上，仿生正弦前缘促使分离涡提前产生，但强度下降，尽管较弱的分离涡使得升力峰值有所损失，但显著降低了阻力和俯仰力矩峰值，抑制了动态失速。同时仿生前缘抑制了二次分离涡的产生，使得下俯过程载荷变化平缓。前缘波峰越大或波长越小，上述趋势越明显。

3 运动参数与来流参数的影响

为了将仿生前缘应用于工程实践，需要进一步探讨其工作范围。本文针对动态失速中最重要的运动参数(平均迎角、迎角振幅、折算频率)以及来流参数(马赫数)，研究其对动态失速特性的影响以及仿生前缘在多种工况下的动态失速控制效果。采用仿生前缘翼A025W5与原型翼进行对比，参考工况为：α=10°+10°sin(ωt),k=0.1,Ma=0.3,Re=3.92×106。影响参数分析只改变所分析参数，其他参数和参考工况一致。

3.1 平均迎角

图18 不同平均迎角下的气动力系数Fig.18 Aerodynamic coefficients at different mean angles of attack

3.2 迎角振幅

图19给出了迎角振幅(αm)分别为5°、10°、15°时原型翼和仿生翼的升力系数、阻力系数及俯仰力矩系数迟滞回线。随着迎角振幅的增加，动态失速特性增强，各气动系数迟滞效应更加明显，反映在各气动系数峰值增加以及流动再附现象推迟。在低迎角振幅情况下(αm=5°)，载荷次波峰未出现，当迎角振幅增加，二次前缘分离涡加强从而产生载荷次波峰，仿生前缘能够在一定程度上抑制二次分离涡与载荷次波峰的出现，缓和载荷变化。仿生前缘在3种迎角振幅下都能有效抑制俯仰力矩峰值，不同振幅下其减小量基本一致，升力峰值的损失也几乎不受迎角振幅的影响，但阻力峰值的减小量在迎角振幅较小时(αm=5°)降低。

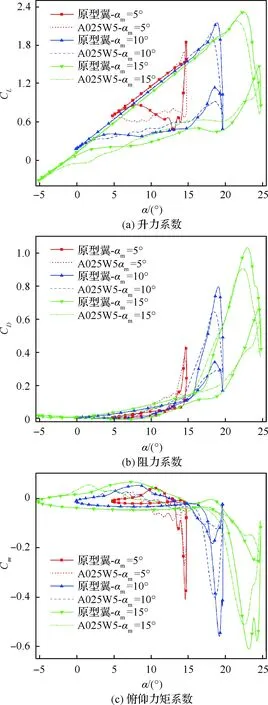
图19 不同迎角振幅下的气动力系数Fig.19 Aerodynamic coefficients at different amplitudes of angle of attack

3.3 折算频率

前飞直升机旋翼的截面通常情况下的折算频率在0.03～0.1之间，据此本文针对3种不同折算频率(k=0.04、0.07、0.10)进行了动态失速模拟，升力系数、阻力系数和俯仰力矩系数的结果如图20所示。首先，折算频率的增加使得动态失速程度加深，迟滞环面积显著增大，气动载荷峰值及所对应迎角增加并且再附迎角减小。随着折算频率的增加，仿生前缘动态失速控制效果相对减弱，反映在俯仰力矩峰值的减小量和阻力峰值的减小量降低，尽管升力峰值损失也减小。另外，仿生翼型气动载荷峰值的出现始终提前于原型翼，随着折算频率降低，这种提前效应愈发明显。

图20 不同折算频率下的气动力系数Fig.20 Aerodynamic coefficients at different reduced frequencies

3.4 马赫数

自由来流速度在直升机桨叶不同半径处差异很大，为了探讨来流速度对动态失速特性及仿生前缘动态失速控制的影响，本文计算了Ma分别为0.3、0.4和0.5下的原型翼和仿生翼的动态失速特性，结果如图21所示。随着来流速度增加，临界逆压梯度减小[25]，前缘分离更易发生，导致前缘分离涡提前生成并向下游运动，又因为大来流速度下分离涡更容易耗散、脱落，因此涡强度减弱，气动系数峰值减小。3种马赫数下仿生前缘都能有效实现阻力峰值和低头力矩峰值的抑制，随着马赫数增加，阻力峰值和俯仰力矩峰值的减小量先基本不变后降低，升力峰值损失也展现相同趋势。