滑翔飞行器弹道规划与制导方法综述
2020-03-02张远龙谢愈
张远龙,谢愈
国防科技大学 智能科学学院,长沙 410073
滑翔飞行器作为高超声速飞行器的一种典型代表,因为特殊的气动构型设计,其升阻比较传统升力式飞行器要大很多,因此可以仅依靠气动力控制实现长时间远距离的机动飞行。由于飞行速度快、机动突防能力强、命中精度高以及飞行距离远等突出优势,滑翔飞行器已经成为当前航空航天领域的主要研究热点之一。作为控制飞行器轨迹的大脑,围绕滑翔飞行器开展的弹道规划与制导控制方法研究更是当下各国学者关注的焦点。
滑翔飞行器的弹道规划与制导方法一直以来都是学者们研究的重点和难点,既要满足高速飞行过程中的强耦合、快时变以及强非线性的运动约束关系,同时还必须限制飞行过程中的最大动压、最大过载以及峰值驻点热流,以免产生过大力矩或高温破坏结构,损毁飞行器。复杂一些的飞行任务,还需要考虑航路点、禁飞区约束等。通常来说,滑翔飞行器有两种再入方式:从天基平台释放后再入和从地面通过助推器发射到一定高度后再入。以助推-滑翔式飞行器为例,飞行器从发射到命中目标点依次经历了主动段和再入段两个不同的飞行阶段[1-2]。其中,再入段又可细分为变轨段(或初始下降段,主要考虑热流约束)、滑翔段(主要考虑热流、过载、动压等过程约束,终端约束,禁飞区航路点等横侧向机动任务)以及俯冲段(主要考虑过载、铰链力矩等约束),如图1所示。
本文主要围绕滑翔段的弹道规划与制导方法开展综述,因为滑翔段是滑翔飞行器整个再入过程中飞行距离最长、弹道形式最为灵活、约束最为复杂的飞行阶段,同时也是最能体现滑翔飞行器强机动特性的飞行阶段。因此,滑翔段是飞行器最为重要的阶段,其弹道规划与制导方法的好坏很大程度上直接决定了滑翔飞行器能否顺利完成整个飞行任务。
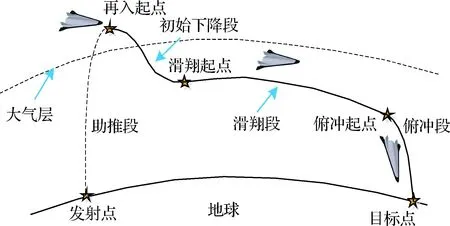
图1 助推-滑翔式高超声速飞行器飞行弹道示意图Fig.1 Typical trajectory of boost-gliding hypersonic vehicle
1 现状分析
一般来说,滑翔段的弹道规划与制导方法主要有两种:基于标准轨迹的制导方法和预测校正制导方法[3]。基于标准轨迹的制导方法是指事先规划一条参考轨迹,然后通过跟踪标准轨迹进行制导。规划的标准轨迹可以是实际三维空间中的一条弹道,或者仅是地面的二维轨迹,甚至可以是表征飞行器运动特性的广义飞行剖面,如阻力加速度-速度(D-V)剖面[4-5]、高度-速度(H-V)剖面[6]以及阻力加速度-侧向升阻比-能量(D-(L/D)sinυ-E)的三维剖面[7]等。标准轨迹规划时,既可以是离线的复杂规划或优化,也可以是在线的快速规划。预测校正制导方法是指基于当前飞行状态,利用数值积分或解析表达式预测出给定控制变量下的终端状态;通过计算预测终端状态与设定终端状态值的偏差调整控制变量,从而实现对飞行轨迹的准确控制。因为在预测终端状态时,通常需要先规划一个参考控制量剖面。因此,预测校正制导方法也可看作是一种广义的规划与制导方法。下面将分别对这两种方法的发展现状进行分析。
1.1 基于标准轨迹的制导方法
基于标准轨迹的制导方法是目前滑翔飞行器弹道规划与制导领域应用最为广泛的一种方法,而其中又以基于标准阻力加速度剖面的跟踪制导方法最为著名。自从20世纪70年代在航天飞机上成功实现以来,基于标准阻力加速度剖面的跟踪制导方法一直受到学者的追捧和喜爱,目前已经发展成了滑翔飞行器制导方法的标杆。其核心思想主要包括以下几个部分[3]:
1) 飞行走廊模型的建立
在参考迎角剖面给定的基础上,将滑翔飞行过程中的峰值驻点热流密度、最大动压以及最大过载等典型过程约束转换成关于D-V的函数,确定走廊的上边界。同时,以滑翔段飞行器保持准平衡滑翔飞行条件作为软约束,建立滑翔飞行走廊的下边界。通过建立飞行走廊约束边界,确定了飞行器可行弹道规划的边界,为规划标准阻力加速度剖面提供了依据。
2) 标准阻力加速度剖面规划
在建立的约束走廊内,选择合适的函数设计参考飞行剖面。通过分析飞行器滑翔过程运动特性,经典航天飞机再入制导方法将标准剖面分成了5个部分,即温控段、过渡段、准平衡滑翔飞行段、过渡段以及线性能量变化段[5]。温控段标准剖面设计的重点是控制飞行器初始时的峰值驻点热流,准平衡滑翔飞行段的设计目的在于尽可能使飞行器进行长时间的准平衡滑翔,而线性能量变化段则是考虑到飞行器在末段由于速度倾角过大产生的航程预测损失严重,因此将D-V飞行剖面改为D-E剖面,提高航程控制精度的同时平滑高度变化。当选定标准剖面形式后,根据阻力加速度与航程的对应关系,迭代确定满足航程约束的参考剖面。
3) 侧向横程控制技术
为了确保满足终端位置精度要求,除了利用标准阻力加速度剖面控制总航程外还应控制飞行器的横程或航向,因此设计了漏斗型的方位角误差走廊决定侧向倾侧反转的时机和符号。当飞行器航向角与视线方位角的差始终保持在设计的误差走廊内时,飞行器的航向将渐进收敛到视线方向,从而通过调整误差走廊的漏斗形状就可获得满意的终端横程精度。
4) 跟踪器设计及标准剖面更新技术
实际飞行与设计的标准情况之间总存在偏差,如飞行器本体在安装、制造过程中不可避免地引入系统误差,加表和陀螺仪测量过程中产生的工具误差,以及实际大气、地球模型等无法精确测量和准确获取而产生的模型偏差等等。由于这些偏差的存在,势必造成实际弹道与标准弹道发生偏离。为了确保飞行器能沿标准弹道完成飞行任务,通过求解关于阻力加速度的动力学方程,建立阻力加速度二阶导数与控制量倾侧角的对应关系;然后利用反馈线性化等方法设计比例-积分-微分(PID)形式的控制器求解跟踪参考阻力加速度及其一阶变化率所需的控制量大小,从而实现对参考飞行剖面或者标准轨迹的跟踪。同时,为了进一步消除实际弹道与标准弹道的偏差,每隔一段时间对标准剖面进行更新,从而提高终端位置的控制精度[4-5]。
虽然现有航天飞机再入制导方法已经可以较好地完成飞行任务,但是仍存在很大的改进空间,主要集中在标准剖面规划、侧向运动控制、轨迹跟踪控制器设计等方面。因为飞行器在滑翔段一直保持无动力飞行,飞行器的机械能必然单调递减。此外,由于能量同时包含了速度和高度信息,因此直接规划D-E剖面比传统D-V剖面在控制高度、速度上更具有优势[8]。有的学者甚至利用能量同时包含高度和速度的特性,将原三自由度的6个微分方程降维到关于能量的5个方程,从而提高了参考轨迹生成和剖面规划的计算效率。为了进一步改进参考剖面的生成效率和适应性,Lu等[9]通过参数化方法将标准D-V剖面分为多个线性小段,并建立以最小吸热量为性能指标的优化函数进行快速优化计算。而Leavitt和Mease[10]则将飞行走廊最大和最小边界的加权值作为标准剖面,通过调整权重系数即可快速产生所有可行解,从而极大降低了标准剖面生成的计算量消耗。在侧向运动控制上,由于飞行器在接近滑翔目标点时视线角迅速接近180°,而航向角的变化势必难以赶上视线角,从而造成传统航向误差走廊控制方法的失灵。因此,有的学者提出了一种基于横程误差走廊的侧向控制方式[11]。但有的学者则认为采用误差走廊的控制方式产生了太多倾侧反转且次数不可控,设计了一种通过迭代终端横程精度确定反转时机的侧向控制方法。这种方法仅需一次反转就可以到达目标点,有时为了确保终端控制精度,在末段靠近目标点某一位置增加一次反转[12]。对于剖面跟踪制导方法,Mease和Kremer利用非线性反馈控制律设计了新的跟踪控制器,发现传统航天飞机再入跟踪制导方法是这种方法的局部实现[13]。Lu[14]则是借助滚动时域控制,重新设计了一种有效的非线性跟踪控制器。由于火星大气密度仅为地球的1/100左右,当飞行器进行火星再入时受到的不确定性干扰更为严重,对再入制导方法的要求也更高。为此,Talole等[15]利用干扰观测器对不确定性影响进行估计和补偿,提高了制导系统的鲁棒性和适应性。相对来说,自抗扰控制技术除了对误差的估计和补偿外,还对参考输入进行了平滑,并且采用非线性组合方式获得控制律。因此,Xia等[11]在传统D-E剖面跟踪制导的基础上融合了自抗扰控制技术,设计了一种鲁棒性更强的跟踪控制器。
值得一提的是在对标准剖面跟踪制导方法改进的过程中,Mease等提出的演化加速度制导(Evolved Acceleration Guidance Logic for Entry, EAGLE)[16]方法表现较为突出。针对传统阻力加速度剖面由于未考虑轨迹曲率而采用大圆弧假设引起的航程计算误差问题,EAGLE通过将标准剖面规划转换为轨迹长度和轨迹曲率两个子问题进行求解。首先根据大圆弧假设得到的总射程解算初始阻力加速度剖面,并由此计算考虑轨迹曲率影响后的实际射程,然后调整阻力加速度剖面直至满足轨迹长度要求。同时,侧向倾侧反转时机在求解轨迹曲率子问题时作为待定参数,通过迭代搜索使其满足终端横程和航向约束要求[17]。在参考剖面跟踪上,将解算轨迹曲率子问题得到的航向角剖面和规划的阻力加速度剖面一起作为需要跟踪的参考剖面,通过分别设计PD控制器跟踪参考阻力加速度剖面和航向角剖面获得倾侧角大小,再将两者的加权值作为实际控制的倾侧角。显然,采用EAGLE方法获得的弹道有效提高了终端横程控制精度,美国马歇尔航天仿真中心(Marshall Aerospace VEhicle Representation in C, MAVERIC)的仿真结果也证明了这一点[18]。进一步,本文作者团队[19]将这一剖面规划方法拓展到考虑航路点和禁飞区约束的复杂飞行任务规划中。
事实上,传统的航天飞机再入制导方法,尤其是基于标准剖面的弹道规划方法行之有效的一个重要前提是事先给定优化的参考迎角剖面,从而飞行器的控制量仅有倾侧角。之所以要将迎角剖面事先给定,一方面是飞行器再入时,尤其是初始再入段产生的气动热十分严重。为了控制驻点热流,确保再入时飞行器不被烧毁而必须将迎角限制在一个合理的范围。另一方面,当同时调整迎角和倾侧角控制飞行轨迹时,由于纵、侧向运动耦合较为严重,难以找到稳定收敛的双通道轨迹控制方法。因此,为了确保飞行器安全和降低参考弹道的设计难度,在标准剖面设计之前先通过优化确定参考的迎角剖面。这种策略在早期滑翔飞行器仅需实现从起点到目标点间的典型任务下是可行且得到广泛认可的。但是,随着科技的进步和人们对再入问题认识的深入,对滑翔飞行器完成任务的复杂程度也赋予了更多的期望,尤其是在充分发挥其横侧向机动飞行能力上提出了更多的要求。所以,采用固定迎角剖面的传统标准剖面规划与制导方法限制了飞行器机动能力的发挥,已成为了制约飞行器弹道规划与制导技术进一步发展的一个障碍。早在1999年时, Mease等[20]就曾将传统航天飞机的标准剖面规划方法拓展到三维空间并应用到可重复使用飞行器(Reusable Launch Vehicle, RLV)的再入返回试验中。由于拓展到三维空间,考虑侧向运动的再入走廊将会比传统走廊的形式更复杂且更难计算;同时,迎角得到释放后的标准剖面设计也更加困难。虽然Mease等将剖面设计转换为再入走廊内的优化问题进行求解[21],但复杂的计算量仍是这一方法得到应用的重要瓶颈。后来文献[22]在Mease等的基础上,提出了一种分层策略的三维剖面规划方法。通过分别求解纵、侧向的约束走廊,按照先确定纵向剖面后求解侧向剖面的顺序生成初始三维剖面;然后,将获得的纵、侧向剖面利用侧向降阶运动模型进行反复迭代,直到满足终端纵横程要求。由于规划的剖面已进行参数化,仅需迭代几个关键参数就可以获得满足需求的三维剖面,从而大大降低了计算量。随后,何睿智等[23]基于确定的纵、侧向飞行走廊,将基于分层策略的三维剖面规划方法应用到覆盖区域的计算中。从可供查阅的文献来看,目前关于三维剖面的弹道规划与制导方法研究还较少,仍有待进一步深入研究。
除了基于阻力加速度剖面的跟踪制导方法外,基于高度-速度(H-V)或高度-能量(H-E)剖面的跟踪制导方法也是标准剖面跟踪制导方法的典型代表。与基于D-V的跟踪制导方法类似,基于H-V的跟踪制导方法同样需要先将过程约束转换为关于H-V的飞行走廊,然后再在走廊内规划满足任务要求的标准剖面生成需要的参考弹道,通过纵向剖面跟踪器和侧向方位误差走廊同时完成整个飞行轨迹的控制任务。由于迎角剖面事先给定,因此D-V剖面或D-E剖面可以和H-V剖面或H-E剖面进行相互转换。事实上,为了获得设计剖面与航程的对应关系,当规划好标准H-V剖面后仍需要先求出对应的D-V剖面以确定总的飞行航程。但这种方法对于高度变化比较敏感的飞行器来说,基于H-V剖面的跟踪制导比基于D-V剖面的跟踪制导效果更好。而且,在H-V空间内易于得到闭环弹道解析解,从而使采用H-V剖面的跟踪制导方法求解效率更高[24]。
1.2 预测校正制导方法
与基于标准剖面的规划与跟踪制导方法不同,预测校正制导方法[25-26]不需要依赖标准剖面或轨迹,直接基于当前状态不断预测轨迹或终端状态而对控制量进行修正完成轨迹控制任务。因此该方法的核心思想主要包括两部分:如何基于当前状态实现轨迹或终端状态预测和根据预测弹道修正控制量。根据弹道预测所采用的方法,预测校正制导方法分为解析预测校正和数值预测校正制导两种。
1) 解析预测校正制导方法
自从20世纪80年代开始解析预测校正制导方法就已经在火星探测项目中得到了广泛应用,比如Bryant等[27]和Masciarelli等[28]分别基于参考阻力加速度-高度建立的解析预测校正制导律应用于火星再入问题的精确着陆和返回轨道设计。为了增强算法的适应能力和鲁棒性,后来Hanak等[29]在文献[27-28]的基础上又进行了改进。解析预测校正的关键在于预测模型的建立。因此一旦预测模型不同,即使是同一个问题也将会产生不同结果。比如同样是火星精确着陆问题,Lafontaine等[30]基于常值飞行路径角和不旋转火星模型进行弹道预测,而Levesque和Lafontaine[31]则是在不旋转火星模型下,通过建立飞行路径角与大气密度的比例关系实现轨迹预测。可见,在建立预测校正制导模型时,都不同程度地对原问题模型做了简化和假设,如Tigges和Ling[32]在火星漫步者返回弹道任务设计中使用的高度变化率为常值假设和Lafontaine等[30]采用的不旋转火星、常值路径角等。对于滑翔飞行器,Xu等[33]给出了一种基于准平衡滑翔条件的解析预测校正制导方法,后来Zhu等[34]则在其基础上,将准平衡滑翔制导与最优控制结合,提出了一种基于能量损耗最优的准平衡滑翔制导方法。
2) 数值预测校正制导方法
数值预测校正制导是电子计算机计算能力不断跃升的一个重要产物。与解析预测校正制导相比,数值预测校正制导可以做到更高精度和准度,但耗费的计算效能也将成倍增加。由于目前计算机的计算能力和优化算法都已经得到了巨大提高,数值预测校正制导已经越来越受到学者的青睐,比如之前Powell[35]将数值预测校正制导方法分别应用于救生舱返回任务面临的不确定性问题和火星探测器轨道设计所产生的大量计算问题,如今都可以利用高性能计算机快速求解。Youssef等[36]、Fuhry[37]、Lu[38]一大批学者已经将数值预测校正制导方法应用于RLV的弹道规划与制导、航天器轨道设计,甚至有的学者还结合神经网络[39-40]、模糊控制[41]、单纯形算法[42]等开展了弹道预测的研究。
上述两类经典制导方法各有优势和不足。一般而言,基于标准轨迹的制导方法需要进行大量的离线计算和标准轨迹参数的存储,且不能适应大范围的散布误差、设计工作量大,但是一旦产生标准轨迹后,其制导所需时间较小,在飞行器能力允许范围内可获得较高的制导精度。预测校正制导方法适应范围广、制导性能好、散布误差对制导性能影响较小,有利于再入自动化,缩短飞行器再次发射时间,降低成本;但是在线计算量大,对硬件要求高[43]。因此,有的学者就提出了将两种方法相结合的混合制导方法[44-47]。比如,胡建学等[44]在研究RLV的滑翔段制导方法时,将滑翔段分为拟平衡滑翔段和线性倾侧段;在拟平衡滑翔段采用基于阻力加速度剖面的标准轨迹制导以提高精度;对于线性倾侧反转段则采用预测校正制导方法,充分发挥预测校正制导方法的计算效率,同时兼顾了高精度要求。王青等[45]在研究滑翔段时,则是先产生标准轨迹,然后基于剩余航程随能量单调变化的特性将标准轨迹进行分段,最后分段进行在线预测校正制导。同样是先产生标准轨迹后获得分段航路点的混合制导方法,但是王俊波等[46]则是通过分段在线规划的方法进行制导,同时要求新校正后的标准轨迹在通过航路点时必须同时满足位置、速度以及高度要求。此外,文献[47]结合标准轨道法,通过对有限几个特征点位置上引入预测制导,形成了一种基于最优化问题的混合制导方法;该方法有效减小了预测制导指令的解算时间,进一步降低了落点误差。
2 当前研究的热点与难点
从早期的Apollo再入制导开始算起,滑翔弹道规划与制导方法发展到现在已经历了几十年。从最初的慢慢探索到形成以航天飞机再入制导方法为标杆,再到如今基于标准剖面的跟踪制导和预测校正制导方法齐放以及针对大升阻比滑翔飞行器运动特性而渐渐发展的准平衡滑翔制导方法,人们对滑翔弹道规划与制导问题的认识在不断深入,研究的热点和难点也在不断发展和变化。目前,关于滑翔弹道规划与制导方法的研究热点与难点主要有以下几个方面。
2.1 多约束复杂任务条件下弹道规划与制导技术
由于地缘政治、军事斗争和防御等实际问题的存在,滑翔飞行器在进行长时间远距离飞行时需要避开一些特定的禁飞区或通过某个特定的测控区域(或航路点)进行辅助导航定位或执行特定飞行任务。因此,滑翔弹道规划与制导方法的研究除了需要考虑常规的驻点热流、动压以及过载等约束条件外,还应满足航路点和禁飞区等复杂任务的需求。因为可行弹道的生成本身就需要克服高动态、强耦合以及多约束等交织的困难,额外增加的航路点约束如果得不到合理规划,则会导致顾此失彼,难以同时兼顾航路点和目标的要求。禁飞区约束的满足则更加困难。因为航路点仅是增加了一个位置约束,而禁飞区要求则需要实时监测所有弹道状态避免通过特定区域。一方面,禁飞区约束的增加极大压缩了可行弹道的求解空间,对飞行器的侧向机动性能提出了更高要求;另一方面,为了成功实现禁飞区规避、减小过多能量损耗,可行弹道生成时应尽可能沿禁飞区边界飞行,即需要通过一系列特定的“航路点集合”。因此,相比于航路点,学者们在禁飞区规避问题的研究上投入得更多,比如Jorris[48-49]从最优控制角度出发进行求解,而Xie等[19]、赵江等[50]、王青等[51]、Zhang等[52]以及郭洁等[53]采取的基本思路则是纵向采用规划标准阻力加速度剖面满足总航程要求,同时将传统的固定侧向航向角误差走廊改进为考虑航路点和禁飞区约束的动态侧向方位误差走廊,有效提高了基于标准阻力加速度剖面的弹道规划与制导方法适应性和可靠性。可见,在传统定迎角剖面框架下,通过规划纵向弹道满足总航程需求而调整侧向倾侧反转时机实现多约束复杂条件下弹道规划与制导方法的研究工作已经开展了很多,而将迎角剖面约束解除后的多约束复杂条件下标准剖面跟踪或预测校正制导则才刚开始进行研究。比如,何睿智在文献[54]中给出了一种基于三维加速度剖面实现禁飞区规避的弹道规划方法。但是,文中仅对飞行器不需要进行倾侧反转情况下的弹道规划进行了研究。此外,朱建文等[34]基于准平衡滑翔最优制导,在确保纵向满足能量最优的前提下,采用侧向航向角沿视线方向飞行的策略实现禁飞区规避。但是这种策略需要飞行器在经过禁飞区参考点后立即转向下一个目标点飞行,控制量切换瞬间容易出现跳变,而且存在切换后触碰禁飞区的风险。
实际飞行环境下的地理约束可能会更复杂。除了传统方法研究时大多采用的无限高圆柱形禁飞区外,文献[55]还给出了一种基于植物触手思想的弹道规划方法,研究了针对多种复杂构型下的禁飞区规避问题。但这种方法需要依赖大量数值仿真,计算量较大。可见,由于参考迎角剖面约束解除而引起的飞行机动能力增加和耦合性增强,以及任务要求更为严苛下的禁飞区约束弹道规划与制导方法还存在很多的技术问题需要解决,仍是当下继续深入研究的一个重要发力点。
2.2 弹道快速优化及在线生成技术
弹道快速优化技术及在线生成一直以来都是学者研究的热点[56],如2003年Shen和Lu就声称可以在桌面级电脑上实现2~3 s产生一条25 min左右的高超声速滑翔飞行弹道[57]。但是这种方法产生的弹道并没有考虑航路点和禁飞区约束的影响,而且对于飞行速度超过马赫数20以上的滑翔飞行器而言,2~3 s将产生很大的位置偏差。当然,随着计算机速度的飞速发展,2003年需要2~3 s才完成一次弹道生成的方法如今可能已经被大大缩减到毫秒甚至微秒级。但是,复杂约束条件下弹道快速优化,甚至在线生成的困难却依然存在。一方面是利用这类优化算法求解时,需要给出合理的迭代初始条件或弹道,否则甚至无法确保优化问题准确收敛;另一方面,这类优化方法,如遗传算法[58]、粒子群算法或者其他优化算法等大多只是对个别控制量参数或者飞行剖面参数进行优化,得到的只是局部最优解。一旦问题的复杂度增加,比如考虑多个航路点和禁飞区并存或极端性能考核下的优化弹道时,盲目增加优化参数不仅使计算量成倍增加,甚至还会由于陷入局部最优而无法获得可行解。近来,随着数值优化算法的迅速发展,一大批先进的优化算法正在或已经被用于解决复杂约束条件下的再入弹道快速生成。其中,以同时对状态量和控制量进行全局优化搜索的伪谱法[59]的弹道优化设计方法较多。比如,Yu等[60]针对火星再入轨迹优化问题,利用伪谱法设计了一种考虑干扰和初始状态偏差的再入轨迹,而Ma等[61]则将高斯伪谱法应用于月球上升段常推力下的燃油轨迹优化设计。针对禁飞区和航路点等复杂约束条件下的弹道优化问题,Zhao和Zhou[62]基于分段高斯伪谱法优化的策略进行求解。Zhang等[63]则针对有限航程下高超声速飞行器吸热控制问题,利用高斯伪谱法给出了一种多约束复杂条件下弹道规划方法。而Miller和Rao[64]则针对包括动力上升段、离轨段、再入段等多段复杂约束条件下的轨迹优化问题,应用高斯伪谱法进行求解。可见,伪谱法已基本被应用到再入轨迹优化设计问题的各个方面,但是计算量大、甚至有时难以得到满意收敛解的问题一直存在。因此,Yang和Qi[65]针对伪谱法求解再入轨迹优化问题时网格节点迭代计算量大的问题,研究给出了一种网格精炼技术。Burchett[66]基于高斯伪谱研究了线性或准线性方程的弹道快速设计,并用线性二次型调节器(LQR)实现跟踪制导的目标。Jiang和Li利用粒子群和高斯伪谱法协同优化实现了兼顾全局最优性与高精度的目标,即先利用粒子群优化算法产生初始弹道,再通过高斯伪谱法进行优化求解[67]。除了伪谱法之外,还有诸如Akima样条插值[68]、多分辨率技术[69]、模糊控制[70]、鸽子启发式算法[71-72]等等。事实上,包括伪谱法、Akima样条插值以及多分辨率技术等在内的这类优化算法在求解轨迹优化设计问题时,其基本思路都是将复杂非线性连续轨迹优化问题转换为离散非线性规划(NLP)问题进行求解,不同之处只是在于其离散方式和迭代搜索策略。但是,当下普遍采用的伪谱法等优化算法暂时还未能实现十分快速甚至在线生成多约束复杂条件下弹道的目标,仍是眼下需要着力研究的一个难点问题。
近来,凸优化技术[73-74]因其快速收敛性而被广泛应用于航空航天领域的轨迹优化。但是,由于轨迹优化设计问题大多是非凸的,为了应用凸优化技术求解就必然需要考虑如何将非凸问题进行凸化。比如,Acikmese团队[75-76]在行星探测器和助推器的动力下降段、返回着陆段都利用凸优化技术进行了轨迹优化设计;Lu和Liu[77-78]针对火箭发射和返回着陆问题,通过将非凸问题转化为二阶圆锥规划问题后进行求解;此外,国内还有如天津大学的Bai团队[79-80]和北航的李慧峰团队[81-82]等也都应用凸优化技术分别进行了轨迹优化设计。这类成功应用凸优化进行轨迹优化设计的问题几乎都具有一个显著特征,即飞行器的动力作为主要控制力而气动力作为辅助甚至忽略。随着研究的深入,近来也有一些学者开始尝试将凸优化技术应用到以气动力为主要控制力的滑翔飞行器再入轨迹优化设计中,比如Liu等[83]、Wang和Grant[84-85]以及Zhao和Song[86]。尽管已经有学者开始进行研究,但就无动力滑翔再入轨迹优化设计问题而言,当前已取得的成果和认识还不够,仍需要继续深入研究。
此外,再入轨迹优化设计问题本身就与飞行器的气动构型、气动力和气动热等问题紧密相关[87]。在飞行器总体设计时就需要统筹兼顾气动布局、结构安全和飞行器的机动能力等诸多方面因素的影响。因此,近来也开始有许多学者开始针对上述多学科优化设计问题开展研究,比如Souza和Nesrin[88]对传统航天飞机再入制导方法存在指令不连续且对大气环境敏感等现象,基于多学科优化设计方法研究了一种解析和数值混合的再入制导方法。Lobbia[89]则在气动分析、总体质量估计、沿弹道气动热分析基础上,设计使飞行器纵程、载荷质量以及升阻比最大的飞行器,而汪文凯等[90]则通过哈密顿分析,研究了兼顾气动热和飞行射程的多学科弹道优化设计问题。可见,通过多学科交叉优化设计,对于提高飞行器性能、加深飞行器认识有较大促进作用,是当下值得继续深入研究的一个方向。
2.3 强不确定条件下高精度强鲁棒制导技术
不确定性一直是困扰滑翔飞行器弹道规划与制导技术的难题,主要包括飞行器本体与飞行环境的不确定性两大类,涉及由于导航装置无法准确获得的飞行器位置、速度以及姿态的不确定性,大气密度不确定性,气动参数不确定性,气动烧蚀引起的结构质量不确定性,甚至某些意外因素引起的气动舵失灵等不确定性。尽管再入制导方法自从航天飞机成功返回到现在已经发展了几十年,但是在工程实践上,即使现在很多专家和学者还是优先考虑基于PID[91]的控制律,以确保任务成功实施的稳定性和可靠性。事实上,目前在理论上研究的很多先进制导方法,比如基于反馈线性化[13]、滑模控制[92]以及基于LQR[93]的跟踪制导等,最后都可以等价为传统PID控制器加修正项的形式。一方面,虽然通过增加这些修正项,在某些情况下理论上确实可以比传统PID控制器有效提高制导精度,但是控制器的收敛域和鲁棒性也相应降低;另一方面,当前研究的这些方法的优异性能大多依赖于精准的数学模型和许多前提条件,而实际飞行中是多种不确定性交织存在的,甚至原先精确匹配问题的数学模型可能由于某种意外而导致无法适用,故而仍使用依赖模型获得优异性能的制导方法则将存在极大风险。因此,为了确保安全起见,当飞行器本体和飞行环境不确定性因素的影响较大时,设计者一般优先选择控制收敛域较大和与模型无关的PID控制器。但是,对于高超弹道跟踪与控制领域的PID控制器,高精度与强鲁棒之间的平衡目前仍难以给出一个较为满意的理论确定方法,故而这也是本文认为当前仍需加强不确定条件下高精度强鲁棒制导技术研究的一个重要原因。
20世纪80年代,韩京清先生率先提出了自抗扰控制器的概念,并于2009年和2011年分别通过了运动控制工业评估和取代了PID控制器首次应用于10条尼龙管挤压生产线的控制[94]。自抗扰控制器主要包括3个关键部分:跟踪微分器、扩张状态观测器以及误差的非线性组合。更为一般的说法,自抗扰控制器由参考输入的平滑器、未知干扰的估计和补偿器以及误差的非线性组合3部分组成。从原理上说,自抗扰和PID控制都属于通过深入挖掘输入输出信息以建立控制器模型而不依赖系统模型的控制方式。但相比而言,自抗扰控制多了跟踪微分器和干扰的估计和补偿器[95],而且采用了更为一般的非线性方式进行误差组合。在收敛域和控制精度方面,理论上比传统的PID控制器更为优秀。因此,Xia等[11]就将自抗扰控制应用于火星再入制导;Talole等[15]则只是将其中的干扰估计和补偿的思想与传统跟踪制导方法相结合,针对强不确定条件下的滑翔飞行器再入制导问题,给出了一种基于干扰观测器的标准剖面跟踪制导方法。此外,为了补偿由于强不确定条件产生的干扰影响,杨俊春等[96]、Zhu和Zhang[97]等则通过气动辨识估计大气与气动系数乘积等方式对设计的再入制导律进行补偿[98-99]。
滑翔飞行器具有强耦合、快时变以及多约束复杂非线性等运动特性,当实际飞行中出现较大本体和环境的不确定性因素影响时,上述这些方法是否还能有效保证误差可靠收敛和控制精度,目前仍没有一个统一而严谨的理论回答。因此,这也是当下仍要进一步深入研究的重要课题。
3 未来可能发展趋势
当下,人工智能技术在全国正如火如荼开展。国家更是在十三五规划和《中国制造2025》等关乎国家科技发展的重大计划中明确将人工智能列为其中一项关键技术。因此,不仅是对于滑翔弹道规划与制导方法而言,而且是对飞行器全飞行阶段的弹道规划与制导方法而言,都应该着力开展基于人工智能技术的弹道规划与制导方法研究。这不仅仅是顺应时代发展的需要,更是事物本身发展的一种自然需求。鉴于本文作者水平有限,下面仅从3个方面阐述基于人工智能技术的未来弹道规划与制导方法的发展趋势。
1) 面向任务的自主规划与制导技术
未来滑翔飞行器应该是只要输入发射点和目标点参数,就能自动实现包括助推段和再入段全程飞行任务自主规划与制导的目标。飞行任务可以是在发射前就装订包含任意多个航路点和任意形式的地理障碍禁飞区约束,也可以是实际飞行中由导航卫星、预警雷达等在线探明的敌方防御区等。飞行器可以实现从任意点到全球范围内任意位置的全方位多角度精确到达。为了确保安全、可靠、有效地实现上述功能,飞行器应具备目标覆盖区域的实时预测能力、可行弹道的在线重规划技术以及高精度强鲁棒自适应制导技术等。
2) 面向大数据的重构制导技术
实际飞行环境错综复杂,任何意外都有可能随时出现。面对实际飞行中本体和环境的各种不确定性因素影响,飞行器应基于人工智能分析包含飞行器动力、控制器执行机构、热防护系统状态、结构等信息获知飞行器当前的健康状态以及周围环境的压强、大气密度等外界环境状态,时刻准备并具有当飞行器某一执行机构出现突然卡死或动力系统工作异常等突发状况时仍能实现飞行任务在线重规划和重构制导的技术。为了实现上述功能,飞行器需要充分挖掘测量和感知的大数据信息,准确评估自身各项部件的健康状态和周边环境信息以确定当前飞行能力边界以及实现控制力的智能再分配,然后再以此为依据进行飞行弹道的在线重规划和重构制导。
3) 面向智能规划与决策的制导技术
当前弹道规划与制导技术主要还是基于环境信息基本已知的情况下,通过地面预先装订飞行方案后交由飞行器的弹道制导与控制系统进行实现。未来,人类的脚步显然不会止步于地球,或月球、火星等近距离的太空探索。当面对深空等未知、未探明或存在强不确定干扰的突发环境时,飞行器只有具备类脑感知和分析技术,才能基于已有各种传统成功规划的飞行任务大数据,智能自主地决策各项新信息和执行新的任务规划,直到完成飞行任务。
4 结 论
围绕滑翔飞行器弹道规划与制导问题展开综述,概述了当前滑翔飞行器基于标准剖面和基于预测-校正思想的弹道规划与制导方法研究现状,分析了当前的研究热点与难点,并结合人工智能探讨了未来滑翔飞行器弹道规划与制导方法的可能发展趋势。本文的研究工作将对解决滑翔飞行器弹道规划与制导的关键技术问题和下一步工作的开展具有参考作用。
