从物理视角欣赏美妙的圆锥曲线
2020-02-29刘文彪
刘文彪
大约在2300年以前古希腊数学家就开始研究圆锥曲线问题,提出了利用平面切割圆锥面可以得到椭圆、抛物线和双曲线.欧几里得在著名的《几何原本》中,还系统地给出了圆锥曲线用焦点和准线方法的统一定义.圆锥曲线问题不但在数学中有完美的理论体系,而且在科学研究和工程技术上也有着广泛的应用.系统、深入地学习和研究圆锥曲线相关知识,对巩固高中课内的数学、物理知识,培养科学探究的兴趣,树立正确的自然观、世界观、科学观具有重要的意义.
1 圆锥曲线的几何定义
如图1,用平面切割圆锥时,平面垂直于对称轴,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到只与圆锥的一条母线平行时,得到抛物线;用平行于圆锥对称轴的平面截取,可得到双曲线.正因为如此,古希腊数学家阿波罗尼曾把椭圆叫作“亏曲线”,把抛物线叫作“齐曲线”,把双曲线叫作“超曲线”.
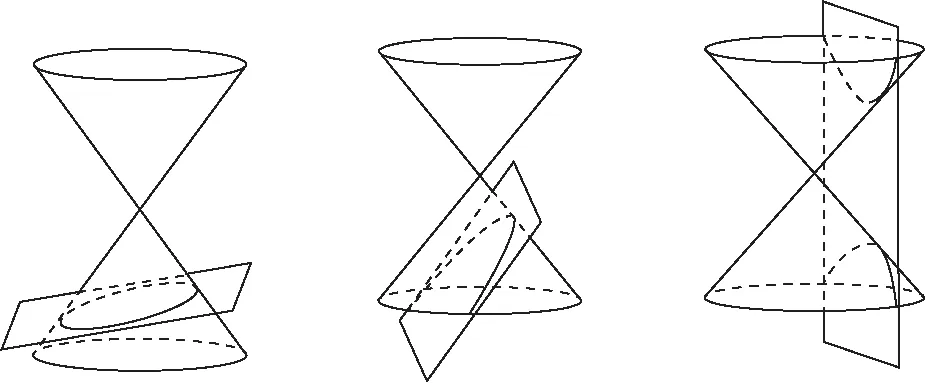
图1 平面切割圆锥面得到椭圆、抛物线、双曲线
如图2,圆锥曲线还可以通过到一定点和到一定直线距离之比是常数的动点轨迹来定义,MF∶MC<1时,M点轨迹为椭圆,MF∶MC=1时为抛物线,MF∶MC>1时为双曲线.到定点(焦点)的距离与到定直线(准线)的距离之商是常数e(离心率).显然,当0
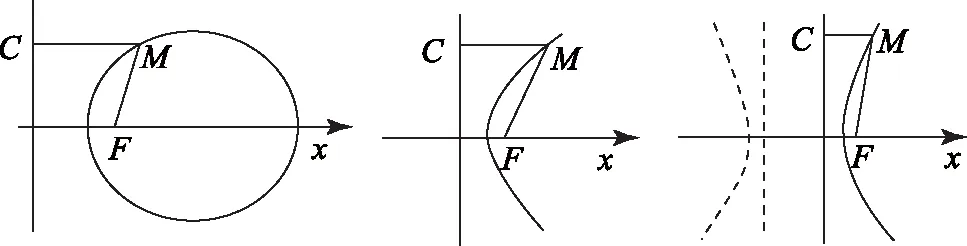
图2 由焦点和准线定义的椭圆、抛物线、双曲线
此外,椭圆上任何一点到其两个焦点距离之和为定值,双曲线上任何一点到其两个焦点距离之差为定值,这也可以作为椭圆和双曲线的定义.椭圆、抛物线、双曲线的上述三种几何定义是完全等价的,而中学教材里为了理论的系统性和规范性利用更多的篇幅介绍和讲述第二种定义.这样更加凸显了圆锥曲线的解析几何特征,使得圆锥曲线自然对应平面直角坐标系下的二次曲线方程,因此圆锥曲线又称二次曲线.
事实上,椭圆、抛物线、双曲线是圆锥曲线的三种主要情形,充分考虑退化和特殊情况的圆锥曲线则有着更加丰富的内容.开普勒提出,圆锥曲线可以看作能够从一个形状连续地变到另一形状,抛物线还有一个在无穷远处的焦点,直线是圆心在无穷远处的圆.因此,椭圆、抛物线、双曲线、圆,以及由两条直线甚至一条直线组成的退化圆锥曲线,都可以从其中一个连续地变为另一个,只需考虑焦点的各种移动方式.椭圆有左右两个焦点F1、F2,若F1固定,考虑F2的移动,当F2向左移动,椭圆逐渐趋向于圆,F2与F1重合时即为圆;当F2向右移动,椭圆逐渐趋向于抛物线,F2到无穷远处时即为抛物线,直至一条直线;当F2从无穷远处由左边回到圆锥曲线的轴上来,即为双曲线;当F2继续向右移动,F2又与F1重合时即为两相交直线.
2 解析几何与二次曲线
笛卡尔的《几何学》提出了解析几何的主要思想与方法,标志着解析几何的诞生.笛卡尔的坐标系是一种思想方法,也是解析几何的根基,使得人们可以用数学方程来研究平面上的曲线,进而认识到代数中二元二次方程的图象就是圆锥曲线.《几何学》使整个数学发生了崭新的变化,笛卡尔也当之无愧成了现代数学创始人之一.继笛卡尔直角坐标系之后,数学家们还给出了平面极坐标系,并能把这两种坐标系相互转换.在这种情况下,表示圆锥曲线的二次方程只需考虑高中通用教材里的几种标准形式.从最一般的二元二次方程出发,经过坐标变换,通过坐标轴的适当平移和旋转,在不退化的情况下总可化为圆锥曲线的标准形式.
抛物线的标准方程为y2=2px(p>0).
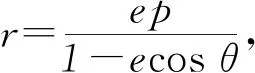
3 神奇的圆锥曲线及其技术应用
椭圆、抛物线、双曲线各有其神奇、独特的光学特性,这些性质被应用于光学、声学、热学、电子学等领域,促进了科学技术的发展和进步,改善了人类的生产和生活.如光学中灯具与望远镜的设计;声学中音乐台的抛物面屏墙、椭圆听音实验;医学电子学中的冲击波排石、椭圆激光消痣;在微波通信、聚热、发电(如太阳灶、太阳炉、太阳能光电站)等领域,也广泛地用到了圆锥曲线尤其是抛物线的“光学特性”.
具体来说,从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上.从抛物线的焦点发出的光,经过抛物线反射后,反射光线都将平行于抛物线的对称轴.从双曲线一个焦点发出的光,经过双曲线反射后,反射光线的反向延长线都汇聚到双曲线的另一个焦点上.椭圆、抛物线、双曲线这些神奇的光学特性,其光路图如图3所示.
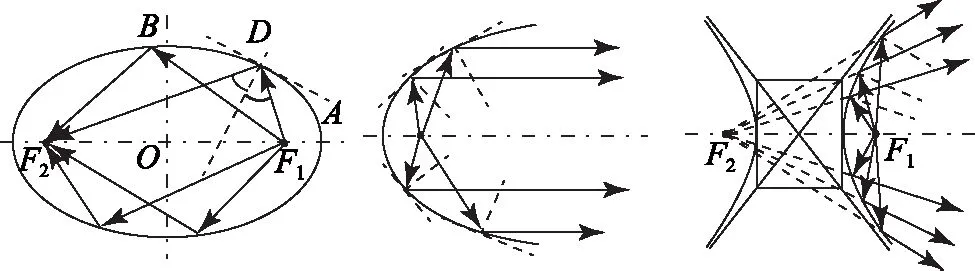
图3 椭圆、抛物线、双曲线的神奇光学特性
由椭圆、抛物线、双曲线绕其对称轴旋转,可得到对应的二维旋转面.此时,原本圆锥曲线对称轴上的焦点就成了二维旋转面在三维空间中具有奇妙性质的焦点.例如,对于抛物面来说,任何一条过焦点的直线由抛物面反射出来以后都将成为平行于轴的直线,因此探照灯反光镜一定要做成旋转抛物面.
圆锥曲线在许多大型拱形、薄壳形建筑上以及大量生产、生活用品制造上都有广泛的应用,这些妙用是由其特殊的形状和内在特性决定的.如根据“双曲线时差定位法”的基本原理,人们发明了当今普遍应用的“全球卫星定位导航系统”.
4 行星椭圆运动和抛物线
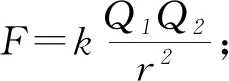
开普勒是德国天文学家,于1571年12月27日出生于一个小市民家庭,从小他就身体欠佳,天花使他成了麻子,猩红热损伤了他的双眼.17岁时他开始攻读神学,于1591年获得神学硕士学位.毕业之后开普勒不顾父母的反对,在奥地利的一所大学里找到了一份自然科学教师的工作,而不是做工作轻松的牧师.30岁时,开普勒写信联系丹麦天文学家第谷,由于他的出色才华而成为第谷的助手.虽然与第谷只合作了10个月,第谷便去世了,但开普勒继承了他留下的宝贵资料.利用第谷多年积累的准确、丰富的观测资料,开普勒发现了行星运动规律,提出了行星运动三定律(即开普勒定律),为牛顿发现万有引力定律打下了基础.
开普勒定律表述如下:
1)所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上.(1609年)
2)行星和太阳的连线在相等的时间内扫过相等的面积.(1609年)
3)所有行星公转周期的平方与它们轨道半长轴的立方之比为常数.(1619年)
在第谷的工作基础上,开普勒还编制成了《鲁道夫星表》,直到18世纪中期这个星表仍然被天文学家和航海家们视为珍宝,它的形式几乎没有改变地保留到了今天.
根据开普勒第一、第二定律,按照牛顿第二定律所揭示的动力学规律,人们给出了在平面极坐标系下做椭圆运动的行星轨道与恒星施与行星的力之间应该满足的微分方程
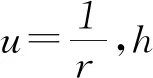
凑巧的是,不但天体运动的基本形式是圆锥曲线.意大利物理学家、科学的先驱者伽利略(1564—1642)研究物体在地面附近的斜抛运动时,发现其轨道竟然也是圆锥曲线的一种,即抛物线.今天我们都知道,行星受到太阳的作用力,与地面上抛出物体受到的重力,本质上都是万有引力.牛顿把地上的运动规律和天上的运动规律统一起来的万有引力,其表现的图景就是抛体运动和行星运动,它们均属于圆锥曲线运动.不仅如此,微观方面,卢瑟福散射中的粒子沿双曲线运动;玻尔的“电子在核外绕核做圆周运动”的量子化轨道也被推广到椭圆运动.
圆锥曲线无论是在数学领域,还是在从物理角度认识自然界最基本的规律中都占有重要的地位,人们对它的研究不断深化,其研究成果又广泛地得到应用.这正好反映了人们认识客观事物的实践和规律,也充分体现了数学之美、自然之美、科学之美的和谐统一.
