一道组合数求和问题的探究

林国红

每年各地的高考题或模拟试题,都会有一些难度相对较大的压轴题,这类考题需要考生有较高的数学思维广度与深度,主要考查考生的理解能力、运算能力等素养,以满足高校对人才的选拔．下面以2019年佛山市理科模拟试卷的第16题为例,进行分析探究,体会其魅力．

1 试题呈现与分析

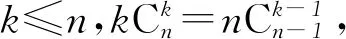
分析本题是关于组合数求和的问题,集组合数的性质、二项式定理、函数、导数等知识于一体,着重对运算能力、化归思想、数列求和思想等内容进行考查，其内涵丰富、解法灵活,具有很好的区分度．

2 解法探究

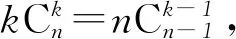
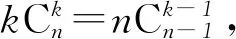
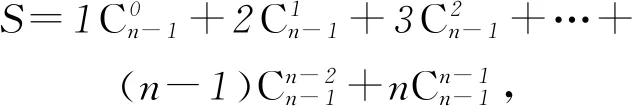
①

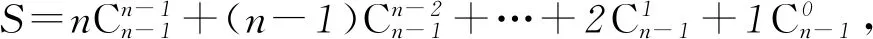
②

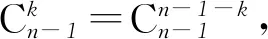
所以S=(n+1)·2n-2,故

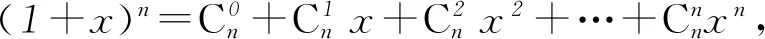
两边同乘以x,得

两边再求导,得

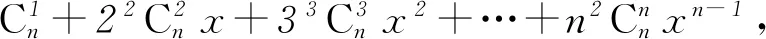
①

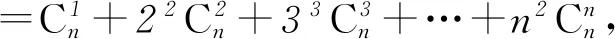
左边=n·2n-1+n(n-1)·2n-2=n(n+1)·2n-2,所以

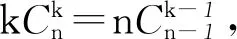
解法4设f(x)=(1+x)n=

则

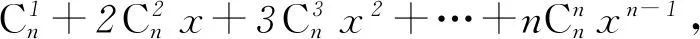
于是

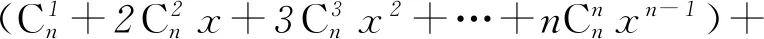
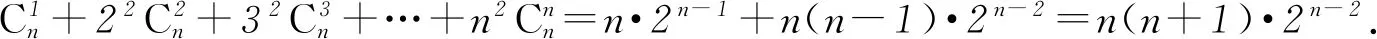
点评 本解法与解法3类似,解法3是在二次求导前先将等式两边同乘x,本解法是在二次求导后直接进行处理．

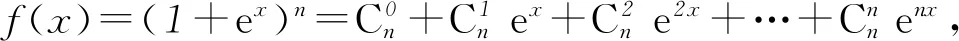
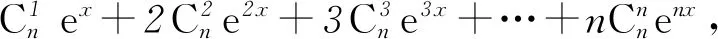
令x=0,得

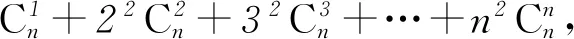
即

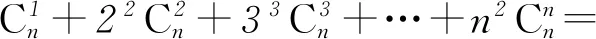
点评 本解法与解法3、解法4类似,都是构造函数,利用二项式定理将函数展开得到二项展开式,再利用导数知识解答．但本法所构造的函数更为巧妙,一次求导后不需要处理,直接二次求导即可．

以上5种解法,从不同的角度出发思考问题,充分体现考题的不拘一格,一道试题往往考查多种能力、多种思想.通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的．

3 试题的推广探究

数学家波利亚曾说:“解题就像采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈．”解答完本题后,同学们还可思考如下问题.

例2设m,n为正整数,如何化简

分析这个问题实际上是例1的推广,可以沿用解法3至解法5的思路进行解答，本文仅介绍解法5的推广．

设m,n为正整数,记

则

于是

这个解法的思路自然,结果看似简单．事实上,当m≥3时,需要求函数f(x)=(1+ex)n的高阶导数,计算量是很大的．那么,有没有更简单的做法呢?通过探索,得到一个组合数求和的递推结论,可以更容易地解决上述问题．

推论设m为任意自然数,n为正整数,记

则有

(1)Sm(1)=1;

(2)Sm+1(n)=n[Sm(n)-Sm(n-1)]．

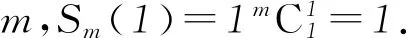
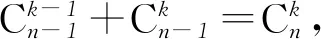
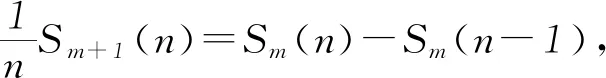
Sm+1(n)=n[Sm(n)-Sm(n-1)]．

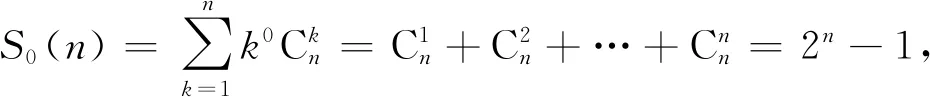
n[(2n-1)-(2n-1-1)]=n·2n-1,

n[n·2n-1-(n-1)·2n-2]=n(n+1)·2n-2,

n[n(n+1)·2n-2-(n-1)n·2n-3]=

n2(n+3)·2n-3,

n(n3+6n2+3n-2)·2n-4,

……

学数学离不开解题,在解题过程中,多探究一题多解,品味解题方法和思维的关键点,从而精学一题,妙解一类．